 |
Абсолютные показатели вариации.
|
|
|
|
Тема 6. ПОКАЗАТЕЛИ ВАРИАЦИИ
1) Абсолютные показатели вариации
2) Свойства среднего квадратичекого отклонения (дисперсии)
3) Методы вычисления дисперсии (СКО)
4) Относительные показатели вариации
5) Виды дисперсий и правило их сложения
Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени.
В отличии от вариации различия значений признака у одного и того же объекта, у одной и той же единицы совокупности в разные периоды или моменты времени следует называть изменениями во времени или колебаниями. Методы их измерения и изучения отличаются принципиально от методов измерения вариации и будут рассмотрены в теме «Ряды динамики».
Причиной вариации являются разные условия существования различных единиц совокупности. Например, вариация оценок на экзамене порождается, в частности, различными способностями студентов, временем, затрачивыемым ими на подготовку, различием социально-бытовых условий и т.д.
Наличие вариации в признаках изучаемых явлений ставит перед статистикой задачи её исследования: определение меры вариации, её измерение, нахождение соответствующих показателей, характеризующих её размеры, выявление их сущности и методов вычислении факторов, её определяющих.
По степени вариации можно судить о многих сторонах процесса развития изучаемых явлений, в частности об однородности совокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления и признаками разных явлений. На основе показателей вариации в статистике разрабатываются другие показатели и методы изучения явлений и процессов общественной жизни – показатели тесноты связи между явлениями и их признаками, показатели оценки точности выборочного наблюдения.
|
|
|
Абсолютные показатели вариации.
Абсолютные показатели вариации характеризуют абсолютную колеблемость (вариацию) признаков и выражаются в тех же единицах измерения, что и изучаемый признак (у дисперсии единицы измерения не записываются).
Размах вариации – это разность между максимальным и минимальным значениями признака.
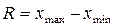
Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.
Среднее линейное отклонение – вычисляется как средняя арифметическая из абсолютных значений отклонений вариант от их средней величины:
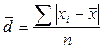– простое,
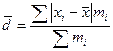– взвешенное.
Среднее линейное отклонение даёт обобщённую характеристику степени колеблемости признака в совокупности.
Простота расчёта и интерпретации составляют положительные стороны данного показателя, однако математические свойства модулей «плохие»: их нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением.
Самый простой способ преодоления этого недостатка – возвести все отклонения во вторую степень. Полученные показатели получили широкое распространение в различных областях знаний, на их основе разработаны новые методы исследования, а также новые показатели количественной характеристики большого класса явлений.
Дисперсия предоставляет собой среднюю арифметическую из квадратов отклонений, т.е. средний квадрат отклонений вариант от их средней величины:
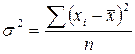– простая,
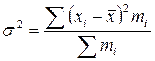– взвешенная.
Средне квадратическое отклонение – корень квадратный из дисперсии:
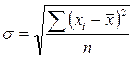– простое,
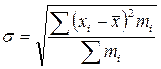– взвешенное.
СКО показывает, на сколько в среднем отклоняются варианты от их средней арифметической.
|
|
|
СКО по величине всегда больше среднего линейного отклонения. Для нормального распределения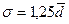 
.
СКО играет важную роль в анализе рядов распределения. В условиях нормального распределения существует следующая зависимость между величиной СКО и количеством наблюдений:
· в пределах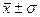 
располагается 0,683, или 68,3%, количества наблюдений;
· в пределах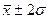 
– 0,954, или 95,4%;
· в пределах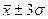 
– 0,997, или 99,7%.
Пример. Группировка акционеров фирмы по размерам дохода
| Группировка акционеров по размеру дохода | Число акционеров чел. (mi) | Середина интервала (хi) | Расчётные данные | |||
| 
| 
| 
| |||
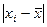
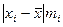
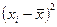
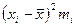
| 90 – 100 | ||||||
| 100 – 110 | ||||||
| 110 – 120 | ||||||
| 120 – 130 | ||||||
| ИТОГО: | Х | Х | Х |
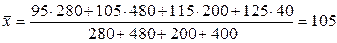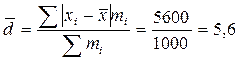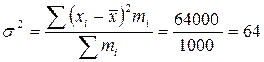д.е.
д.е.
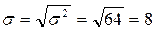д.е.
д.е.
Доход отдельных акционеров отклоняется от среднего дохода акционеров фирмы в среднем на 8 д.е.
|
|
|
