 |
Свойства среднего квадратичекого отклонения (дисперсии).
|
|
|
|
1. СКО от средней арифметической меньше СКО от любой величины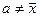 
.
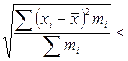
Это свойство минимальности СКО.
2. Если все варианты увеличить или уменьшить на одно и тоже число а, то СКО (дисперсия) не изменится.
, 
.
.
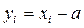3. Если все варианты увеличить или уменьшить в одно и тоже число раз b, то СКО увеличится или уменьшится в b раз, а дисперсия в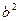 
раз.
, 
.
.
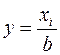4. Если все веса СКО увеличить или уменьшить в k раз, то СКО (дисперсия) не изменится
Если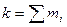 
– сумма всех частей, то можно определить СКО с помощью относительных величин структуры:
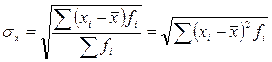, если 
, 
.
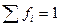Методы вычисления дисперсии (СКО).
1. Метод вычисления СКО по преобразованной формуле.
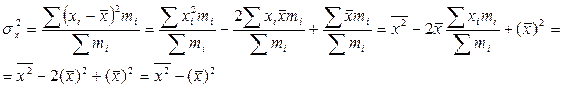
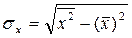
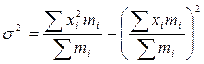
– средний квадрат значения признака или среднее арифметическое из квадратов.
| Группы работников по статусу работы, лет | Число работников | хi | ximi |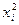 
| 
|
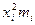
| До 4 | |||||
| 4 -8 | 36*5 = 180 | ||||
| 8 – 12 | 100*12 = 1200 | ||||
| 12 – 16 | |||||
| 16 – 20 | |||||
| 20 и более | |||||
| ИТОГО | Х | Х |
.
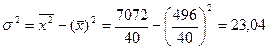
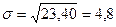2. Вычисление дисперсии и СКО методом моментов.
Метод моментов основан на 2-м и 3-м свойствах СКО и упрощает вычисление СКО.
, 
, 
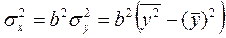
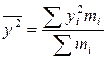В качестве а используют:
· при нечётном числе групп – середину средней группы;
· при чётном – любое из середин 2-х средних групп.
b – величина интервала.
| Группы работников по статусу работы, лет | Число работников | хi |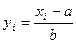 
| yimi |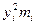 
|
| До 4 | - 2 | - 4 | |||
| 4 -8 | -1 | - 5 | |||
| 8 – 12 | |||||
| 12 – 16 | |||||
| 16 – 20 | |||||
| 20 и более | |||||
| ИТОГО | Х | Х |
.
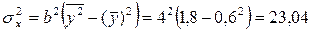3. Вычисление СКО альтернативного признака.
Альтернативный признак – признак, значением которого единицы изучаемой совокупности могут обладать или не обладать.
|
|
|
Например, наличие и не наличие бракованной продукции. Наличие признака обозначают 1, а его отсутствие – 0. Следовательно, альтернативный признак может принимать одно из 2-х значений 1или 0. Вариация альтернативного признака количественно проявляется в значении нуля у единиц, которые этим признаком не обладают, или единицы у тех, которые данный признак имеют. Долю единиц совокупности обладающих значением признака равным 1 обозначают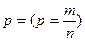 
; долю единиц, не обладающих данным признаком – q. Причём 
.
| ||
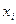
| p | q |
Среднее значение альтернативного признака равно:
.
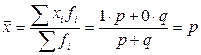Т.е. средней величиной альтернативного признака является доля единиц этого признака.
Дисперсия альтернативного признака определяется по формуле:
.
.
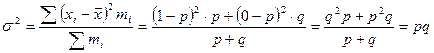Максимальное значение дисперсия альтернативного признака принимает при 
; 
; 
.
Показатели вариации альтернативных признаков широко используются в статистике, в частности при проектировании выборочного наблюдения, обработке данных социологических обследований, статистическом контроле качества продукции и т.д.
Пример: Определим дисперсию и СКО доли организаций, имеющих финансовые нарушения, если проверено 86 организаций и в 37 обнаружены нарушения.
n = 86, m = 37.
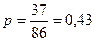, q= 1-0,43 = 0,57.
Следовательно, дисперсия и СКО доли организаций, имеющих финансовые нарушения равны:
;
.
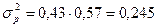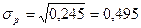Относительные показатели вариации.
Относительные показатели вариации используют для сравнения степени вариации:
1. различных признаков в одной и той же совокупности (вариация заработной платы рабочих и выработки тех же рабочих на предприятии);
2. одного и того же признака в разных совокупностях (вариация заработной платы рабочих на отдельных предприятиях).
Чаще всего они выражаются в % и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности.
|
|
|
Коэффициент колеблемости – это отношение среднего линейного отклонения к средней арифметической:
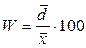
Коэффициент вариации – отношение СКО к средней величине:
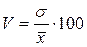
Совокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений близких к нормальному.
|
|
|
