 |
Алгоритм решения задач с помощью принципа Даламбера – схема алгоритма Д54 ПДС
|
|
|
|
С комментариями и примерами
Комментарии
К.2. Рассматриваемый объект принимается либо за МТ, либо за МС, указывается система отсчета, в которой исследуется движение. В случае МС выделяются МТ, АТТ или НМС, входящие в нее.
К.3.4. Для определения ускорений, входящих в формулы для сил инерции МТ, используется алгоритм К01 КМТ (Ч.1 Кинематика) в случае, когда заданы кинематические параметры МТ, и алгоритм Д49 КЭС в случае, когда заданы силы, действующие на МТ.
К.5. На чертеже изображается силовая схема, т. е. рисуются все активные силы, действующие на МТ, силы реакции связи и силы инерции.
К.6. Записывается принцип Даламбера для МТ, используя полученную силовую схему.
К.7. В случае МС или НМС на чертеже изображается силовая схема, на которой рисуются все внешние силы и моменты, действующие на них, в том числе внешние пассивные силы и моменты (реакции связи), силы инерции и моменты сил инерции.
В частных случаях движения – поступательном и вращательном движениях НМС используются формулы для отыскания главного вектора и главного момента сил инерции.
К.8. Записывается вторая форма принципа Даламбера для МС.
К.9. Векторные соотношения 6 и 8 проектируются на оси декартовой системы координат или естественные оси.
К.10. Определяются неизвестные параметры и чаще всего динамические реакции связи.
Пример 1
2 Гладкое кольцо массы m скользит без трения по дуге окружности радиуса r, расположенной в вертикальной плоскости. К кольцу прикреплена пружина жесткости с, закрепленная в точке D. В начальный момент кольцу, находящемуся в положении B0, определяемому углом a0, сообщена скорость V0, направленная по касательной к окружности. Пружина в начальный момент не растянута.
|
|
|
Определить реакцию связи окружности в положении B кольца,указанном на рис. 40 (угол a задан).
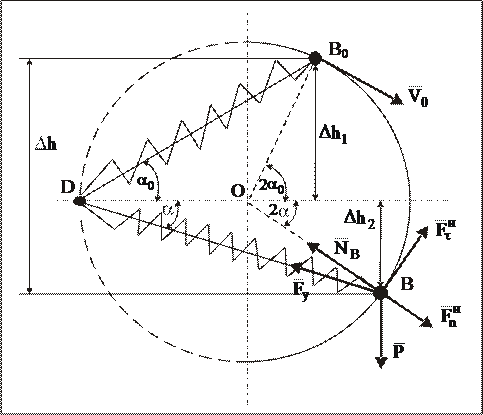
Рис. 40
3 Заданы силы.
4 Д49 КЭС
 |
µ = 3.
j = 1
.
j = 2
j = 3
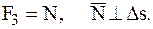
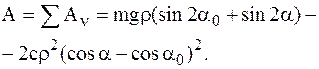
МТ 
, 
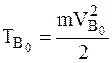
5 
Силовая схема представлена на рис. 40.
6 
.
9 Проектируем соотношение 6 на нормальное направление:
10 Подставляются найденные величины и определяется 
:
11 
Пример 2
2 Вертикальный вал массы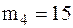 
кг, закрепленный подпятником О и подшипником В, вращается с постоянной угловой скоростью w = 10 с–1. МТ массы 
кг прикреплена к валу стержнем массы 
кг под углом a = 600 к нему. Стержень массы 
кг, параллельный валу, присоединен в середине к валу невесомым стержнем под углом b = 300. Все три стержня расположены в одной плоскости (рис. 41). Геометрические размеры: 
, а=0,3 м, b = 0,5 м, c = 0,2 м.
Рис. 41
Определить реакции подпятника О и подшипника В.
Начало координат берем в точке О, ось Оу направлена по валу, а ось Ох лежит в плоскости стержней и вращается вместе с валом.
7 НМС состоит из МТ массы m1 и трех АТТ: двух стержней массами m2, m3 и вала массы m4.
Силовая схема состоит из четырех сил тяжести: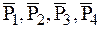 
, реакций опор в точках О и В: 
, силы инерции МТ – 
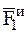и двух главных векторов сил инерции весомых стержней – 
(рис. 42).
Так как вал вращается равномерно, то МТ и элементы стержней имеют только нормальные составляющие ускорения, направленные к оси вращения.
Для МТ сила инерции определится соотношением:
.
Рис. 42
Модуль равнодействующей сил инерции элементарных частиц стержня массы m2 определяется соотношением
.
Точка приложения равнодействующей 
не находится в центре масс стержня С2, так как эпюра сил инерции элементарных частиц стержня (рис. 42) представляет собой треугольник.
Линия действия пройдет через точку К приложения равнодействующей параллельных сил инерции элементарных частиц стержня ЕС1 (Ч.1 Статика). Положение точки К определяется соотношением 
.
|
|
|
Модуль равнодействующей сил инерции элементарных частиц стержня массы m3 определяется соотношением
.
Точка приложения равнодействующей 
находится в центре масс стержня С3, так как эпюра сил инерции элементарных частиц стержня (рис. 42) представляет собой прямоугольник.
8 Принцип Даламбера для плоской системы сил имеет вид:
.
9 Спроектировав первое соотношение 8 на оси координат и записав второе соотношение 8 с учетом силовой схемы (рис. 42), получим:
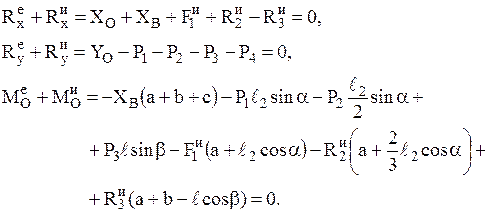
Подставив в эти уравнения значения сил инерции, получим систему уравнений с тремя неизвестными:
10 Подставив в эти уравнения конкретные значения параметров (m1, m2, m3, m4, a, b, c, l, l1, l2, a, b) и разрешив полученную систему уравнений относительно неизвестных реакций опор, получим XО, YО, XB:
Н, 
Н, 
Н.
|
|
|
