 |
В чем состоит суть метода Гомори?
|
|
|
|
а) в преобразовании симплексных таблиц;
б) в экстраполяции неизвестных;
в) в нахождении целочисленного решения последовательными отсечениями от области допустимых решений нецелочисленных точек, пока целочисленная точка не станет угловой (крайней).
В линейной задаче оптимизации распределения ресурсов дополнительные переменные означают:
величины неиспользованных ресурсов
Выберете верное утверждение:
а) область допустимых решений задачи линейной оптимизации может состоять из нескольких разрозненных областей;
б) область допустимых решений задачи линейной оптимизации всегда ограничена;
в) область допустимых решений задачи линейной оптимизации всегда выпукла.
Вычислить длину вектора градиента функции в точке (1,1,1) к целевой функции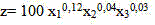 
13
В опорном плане транспортной задачи должно быть следующее количество заполненных клеток:
а) m-n+1;
б) m-n-1;
в) m+n-1; (ДА)
г) m+n+1.
Вычислить значения главных миноров матрицы Гессе функции
z=2x12+x22-x1x2+5x1-6x2+10
7
4
Вычислить сумму множителей Лагранжа для решения задачи на условный экстремум функции Z=х12+х22+х1х3 х1+х2-4=0 х2+х3-6=0 хi>=0
-6
Вычислить значение целевой функции Z=х12+х1х2 в точке условного экстремума
х1+2х2-4=0 хi>=0 в точке (0,2)
0
Вычислить суммарную максимальную прибыль получаемую предприятием от реализации продукции х1 и х2 в моменты времени t= 0; 0,5; 1. Расход ресурсов определен неравенствами 4x1+ 3x2<=12 4x1+ x2 <=8, рентабельность продукции х1 изменяется по закону f1(t)=12t, а продукции x2 f2(t)=8(1-t), параметр t изменяется в пределах [0,1]
Нету ответа
Геометрической интерпретацией целевой функции в задаче линейного программирования с двумя переменными является:
а) точки на плоскости;
б) многоугольник планов;
в) линии уровня.
|
|
|
Граф содержащий маршрут, в который входят все ребра называется:
Гамильтоновым
Граф содержащий маршрут, в который входят все вершины называется:
Эйлеровым
Граф называется взвешенным если:
С каждым ребром графа связано число
Граф называется ориентированным, если для него:
Если для задания ребра важен порядок определяющих вершин
Для нахождения оптимальных смешанных стратегий игры решаются задачи:
решаются двойственные задачи линейного программирования
Для решения транспортной задачи на ЭВМ можно использовать:
а) пакет прикладных программ QSB
б) команду Поиск решения из меню Сервис информационных технологий Exel
Для проведения сбалансированности транспортной задачи необходимо:
ввести фиктивных поставщиков в или потребителей
Для прямой задачи max z =2х1+3х3 x1+x2<=10 x2+3x3<=20
двойственная задача имеет вид:
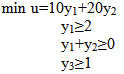
Двойственная оценка численно равна:
г)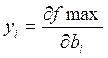 
ДА
Допустимое решение транспортной задачи является опорным, если:
а) оно получено симплексным методом;
б) в этом решении заполненные клетки таблицы транспортной задачи не образуют ни одного цикла (число заполненных клеток таблицы равно (m=n-l), где m — число поставщиков, a n — число потребителей);
в) занятые в этом решении клетки образуют циклы,
Допустимое решение транспортной задачи является опорным, если:
а) …… клетки таблицы транспортной задачи не образуют ни одного цикла и число заполненных клеток таблицы равно (……) где m – число поставщиков, n – число потребителей. ДА
б) в этом решении заполненные клетки таблицы транспортно задачи не образуют ни одного цикла и число заполненных клеток меньше (…….) где m – число поставщиков, n – число потребителей. НЕТ
в) …… в этом решении клетки образуют клетки.
Из инета - Допустимое решение транспортной задачи X=(xij) является опорным тогда и только тогда, когда из занятых клеток таблицы нельзя образовать ни одного цикла.
|
|
|
Для прямой задачи max z=-2х1+х2+3x3 -2x1+3x2+x3+x4=10 x1+ x2-2x3+x5=20
хi>=0 двойственная задача имеет вид
min u=10y1+20y2 -2y1+3y2>= -2 3y1+y2>=1 y1-2y2>=3
Дана транспортная задача: Какое число будет вписано первым в клетку по методу минимального тарифа (эле….)
| А/В | ||
а) 12 или это
б) 5
в) 20
г) 8 или это
д) 9
Дана транспортная задача …………. Какое число будет вписано первым в клетку…….
| А/В | ||
а) 10
б) 5
в) 2
г) 8 (НЕТ)
д) 9
Дана математическая модель. Определить сколько …… будет иметь:
3 (НЕТ)
??
Дана математическая модель и область допустимых решений. Необходимо определить координаты вектора-градиента функции:
f=3x1+4x2 (max)
2x1-x2 ≤8
5х1+3х2≤15
х1≥0 х2≥0
а) (3;4) (ДА)
б) (5;3)
в) (2;-1)
г) (8;15)
Для прямой задачи min z=2х1+3х2+x3 x1+x2+x3<=20 5<=x3<=10
двойственная задача имеет вид:
|
|
|
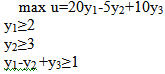
