Задание начальных условий.

Диаметр ёмкости 1: d₁ = 1,5 м

Диаметр ёмкости 2: d₂ = 0,75 м

Высота ёмкости 1: H₁ = 2 м

Высота ёмкости 2: H₂ = 2 м

Площади сечений:

S₁ = 1,766

S₂ = 0,442

Начальный уровень воды в первой ёмкости: h₁⁰ = 1,5 м

Начальный уровень воды в первой ёмкости: h₂⁰ = 1 м

Давление воды: Р₁⁰ = 4*10⁵ Па = 4 атм.

Расходы воды: Q₁⁰ = Q₂⁰ = Q₁₂⁰ =4 м³/ч = 0,0011 м³/с

Начальные значения коэффициентов α₁ и α₂ вычисляются из формул расходов q₁ и q₂ при номинальных значениях. Для этого потребуется также значения констант и параметров:

Ускорение свободного падения: g = 9.81 м/с²

Плотность воды: ρ = 1000 кг/м³

Произведем расчёт:

 

 

 

 

 

 

Часть 1

Построение статических характеристик по каналам P ₁ - h ₁ и α₂- h ₁.

Для построения статической характеристики по каналу P₁-h1 рассчитаем уровень h₁ в пяти точках, то есть при пяти различных значениях давления P_1. Значения P₁ возьмем в окрестности исходного статистического режима, изменяя его на -10%, -5%, +5% и +10% от исходного.

    Кроме того, построим несколько статических характеристик по каналу P₁-h₁ при различных значениях другой входной величины α₂. Её значение также будем варьировать в тех же пределах в окрестности начального статистического режима.

    Таким образом, значения Р₁ и α_2­ для статистических характеристик будут следующими:

 

Р₁¹ = 0.90* Р₁⁰ = 3.6*10⁵ Па            α₂¹ = 0.90* α₂⁰ = 1.414*10^-5

Р₁² = 0.95* Р₁⁰ = 3.8*10⁵ Па           α₂² = 0.95* α₂⁰ = 1.492*10^-5

Р₁³ = 1.00* Р₁⁰ = 4.0*10⁵ Па         α₂³ = 1.00* α₂⁰ = 1.571*10^-5

Р₁⁴ = 1.05* Р₁⁰ = 4.2*10⁵ Па      α₂⁴ = 1.05* α₂⁰ = 1.650*10^-5

Р₁⁴ = 1.10* Р₁⁰ = 4.4*10⁵ Па         α₂⁵ = 1.10* α₂⁰ = 1.728*10^-5

 

Рассчитаем значения уровня в первой емкости h₁ для всех точек Р₁ⁱ при разных значениях α₂ⁱ:

 

Уровень в емкости 1 – h1, м
Р1, Па	3,6*105	3,8*105	4,0*105	4,2*105	4,4*105
α21 =1.414*10-5	1.450	1,531	1,611	1,692	1,772
α22 =1.492*10-5	1,396	1,474	1,551	1,629	1,706
α23=1.571*10-5	1,349	1,424	1,499	1,574	1,649
α24=1.650*10-5	1,308	1,381	1,454	1,526	1,599
α25 =1.728*10-5	1,274	1,344	1,415	1,486	1,557

 

Можно заметить, что значение уровня h₁ в точке начального статического режима равно 1,499, то есть оно отличается от принятого ранее значения h₁⁰ = 1,5 м. Это связано с тем, что при расчетах коэффициентов расходов α₁, α₂, α₃ их значения пришлось округлить. В дальнейшем, примем h₁⁰ = 1.499 м.

 

 

По полученным данным построим графики статических характеристик:

 

 

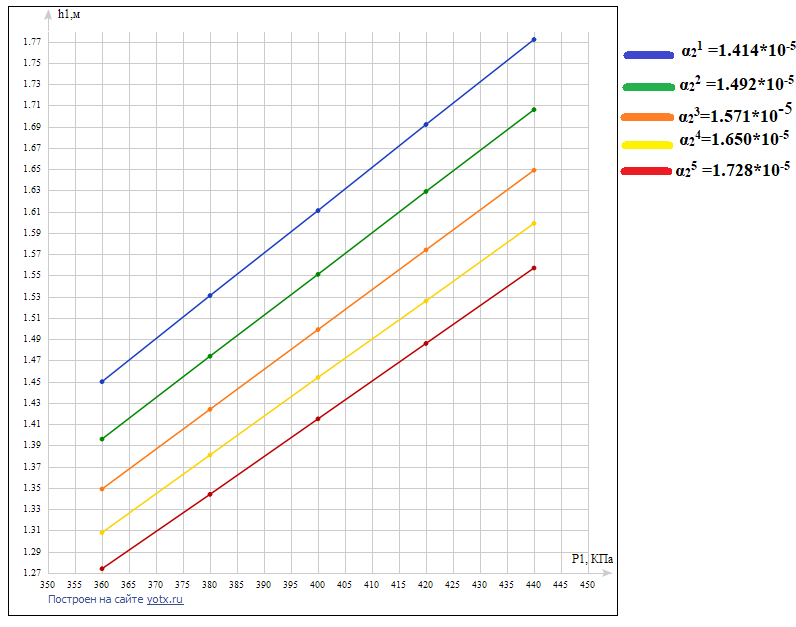
Рис.2 – Статические характеристики по каналу P₁-h₁

 

По графикам можно сделать вывод, что статические характеристики по каналу P₁ – h₁ линейны. С увеличением давления воды P₁ уровень в резервуаре 1 растет. Это объясняется тем, что рост давления воды вызывает уменьшение расхода Q₁ через входной клапан. А так же расход Q₁₂ на выходе из резервуара  меняется, но вода начинает накапливаться в баке и уровень растет. При росте уровня увеличивается давление Р₁ внизу резервуара и, соответственно, меняются перепады давления на клапанах. Расход Q₁ начинает уменьшаться, а Q₁₂ увеличивается, и при определенном значении уровня h₁ они выравниваются и уровень приходит в новое устойчивое состояние.

Так как построено семейство графиков, то можно увидеть, что большему значению коэффициента α₂ соответствует меньший уровень h₁

 

В этом можно убедиться, построив статические характеристики по каналу α₂ - h_1. Для этого не нужно делать новых расчетов - все точки уже есть в предыдущей таблице.

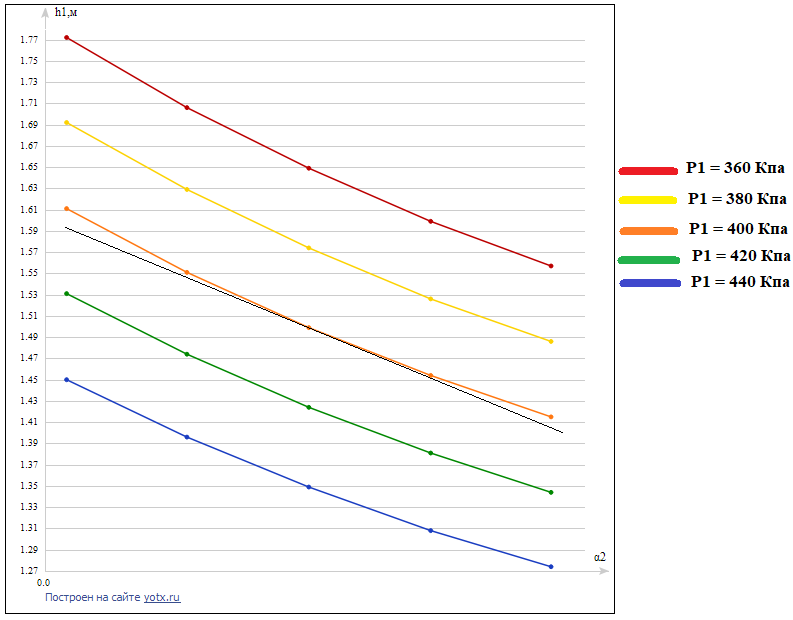
Рис.3 – Статические характеристики по каналу α₂ - h₁

 

 

По данным графикам заметно, что статические характеристики являются нелинейными. Для подтверждения этого на графике проведена касательная в точке минимального статистического режима. Эту прямую можно считать линеаризованной (графическим методом) статистической характеристикой канала α₂ - h₁ в окрестности начального статистического режима. Отклонения прямой от исходного графика на концах диапазона (то есть при α₂ равном 1.414*10^-5 и 1.728*10^-5) составляют около 2 см, что составляет 1,12% от абсолютного значения уровня. Поэтому можно считать, что в заданных диапазонах изменения α₂, линеаризация статистической характеристики в окрестности начального статистического режима допустима.

Графики статических характеристик подтверждают, что при увеличении коэффициента расхода α₂ уровень в первой ёмкости снижается. При увеличении α₂ увеличивается и расход жидкости Q₁₂ перетекающей из первого бака во второй. При этом расход втекающей в бак жидкости Q₁ меняется, а значит, нарушается материальный баланс статики и количество жидкости в баке начинает уменьшаться. При уменьшении уровня снижается гидростатическое давление Р₁ на дне бака, а значит, меняются перепады давлений на клапанах. Вследствие этого, расход Q₁ увеличивается, а расход Q₁₂ уменьшается. При определенном уровне они уравниваются, и емкость приходит в новый статический режим.

Построение статических характеристик по каналам P ₁ – h ₂ и α₂ – h ₂

Исследуем влияние входных переменных Р₁ и α₂ на уровень во второй ёмкости h₂. Для этого нужно рассчитать по уравнению статики значения h₂ при тех же значениях P₁ и α₂. Расчеты приведены в таблице:

Уровень в емкости 1 – h2, м
Р1, Па	3,6*105	3,8*105	4,0*105	4,2*105	4,4*105
α21 =1.414*10-5	0.897	0,946	0,996	1,046	1,096
α22 =1.492*10-5	0,898	0,948	0,998	1,048	1,098
α23=1.571*10-5	0,899	0,949	0,999	1,049	1,099
α24=1.650*10-5	0,900	0,950	1,000	1,050	1,100
α25 =1.728*10-5	0,901	0,954	1,001	1,051	1,101

Для второй ёмкости также значение уровня в исходном статистическом режиме отличается от приятого ранее h₂⁰ = 1 м, по той же причине. В дальнейшем примем h₂⁰ = 0,999 м.

По полученным расчетам построим статические характеристики:

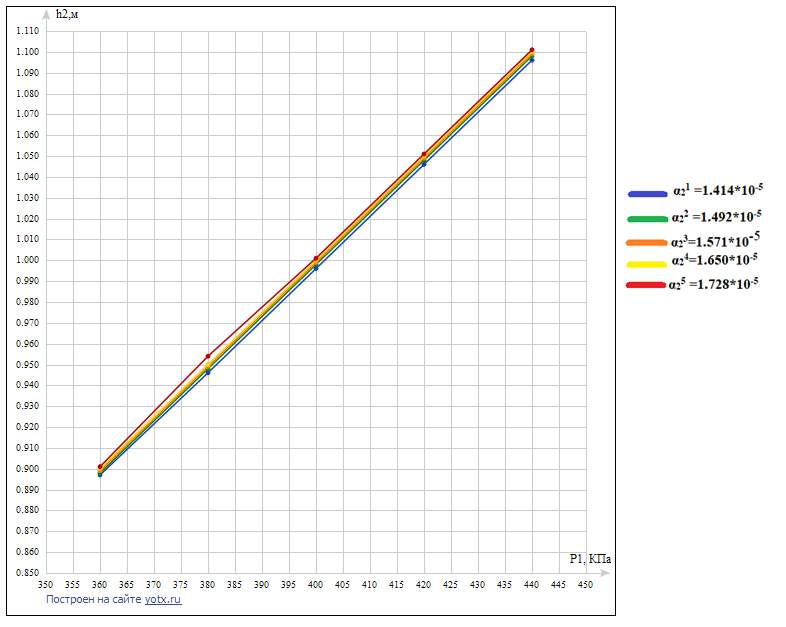
Рис.4 - Статические характеристики по каналу P₁-h₂

Статические характеристики по каналу P₁-h₂ являются линейными. Ранее было показано, что при увеличении давления воды P₁ растет уровень в первом баке. Теперь по графикам статических характеристик видно, что и уровень во втором баке тоже увеличивается Действительно, если уровень h₁ вырос, то увеличилось давление столба жидкости Р_г1, и, вместе с ним, расход воды Q₁₂ поступающий во вторую ёмкость. Баланс статики во второй емкости нарушается и в нем начинает накапливаться жидкость, уровень поднимается. Уровень h₂ растет до тех пор пока давление столба жидкости Р_г2 не вырастет на столько, что расходы Q₁₂ и Q₂ сравняются и объект примет новое устойчивое состояние. Так же по графикам можно сделать вывод, что влияние коэффициента расхода α₂ на уровень h₂ практически отсутствует, так как семейство статических характеристик практически сливается в одну линию.

Убедимся в этом, построив статические характеристики по каналу α₂-h₂:

 

 

 

Рис.3 – Статистические характеристики по каналу α₂ – h₂

Действительно, коэффициент расхода α₂ практически не влияет на уровень во второй емкости. При изменении α₂ в диапазоне +/-10% уровень меняется очень не значительно – визуально в пределах 2 см. Но на графиках все же заметен положительный наклон, то есть при увеличении α₂ уровень h₂ тоже незначительно увеличивается. Действительно, при увеличении α₂происходит увеличение притока жидкости во вторую емкость и уровень должен увеличиваться.

Статические характеристики выглядят линейными, поэтому нет смысла линеаризовать их графически. В то же время, линеаризация формулы статики не приведет к каким – либо значительным погрешностям в заданном диапазоне изменения α₂.

Вывод динамической модели и построение переходных процессов по каналам P ₁ - h ₁, α₂ - h ₁, P ₁ - h ₂, α₂ – h ₂

Для получения уравнения динамики, запишем уравнение материального баланса для одной емкости, когда приток и сток жидкости не равны друг другу. В этом случае происходит изменение количества жидкости в резервуаре со скоростью ΔG (кг/сек):

За время Δt накапливается масса ΔМ, или объем ΔV, который можно выразить из массы с помощью плотности. Также и массовые расходы можно выразить через объемные расходы и плотность:

 

                                           

 

 

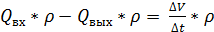
Если применить допущения о постоянстве плотности жидкости во всех точках объекта и во времени, а также допущения о постоянной площади сечения резервуара, формула приобретает вид:

 

Если рассматривать бесконечно малые промежутки времени и приращения уровня, то формулу можно записать с помощью производных:

Получили дифференциальное уравнение динамики резервуара в общем виде. Так как в заданном объекте имеется две емкости, то запишем уравнение динамики для каждой:

 

   

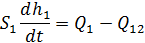
Используя выражения для расходов, получим окончательный вид уравнений. Таким образом, динамика объекта описывается системой двух дифференциальных уравнений:

 

Для решения системы дифференциальных уравнений воспользуюсь средой MathCAD. Решив уравнения численным методом при различных значениях входных переменных Р₁ и α₂, мы получим набор значений уровней h₁ и h₂ в различные моменты времени t и сможем построить переходные процессы.

Переходные процессы будем строить при возмущающих воздействиях по входам Р₁ и α₂ поочередно. Величины возмущений будут равны +(-)5% от начального статистического состояния.

Для решения уравнений в MathCAD введем исходные значения входных переменных, параметров, затем введем новое значение возмущающей переменной, запишем систему дифференциальных уравнений и решим ее с помощью функции «Odesolve».

 

                                  

                                                                     

 

 

 

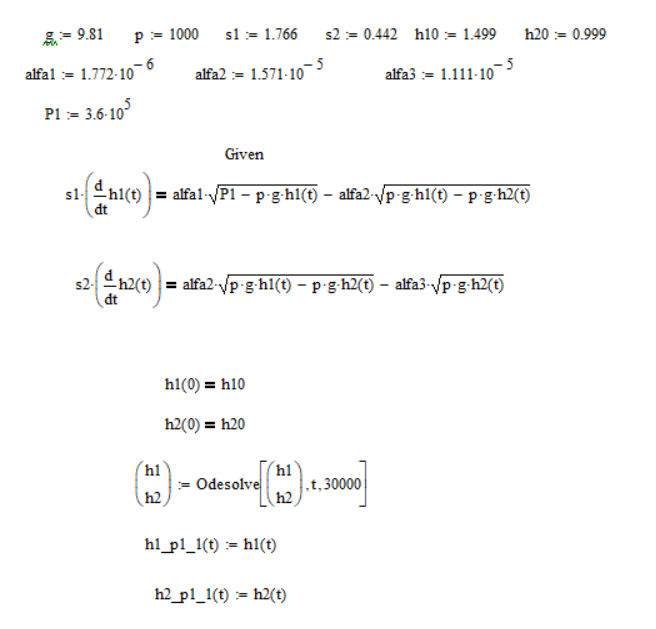
Рис.4 – переходные процессы по каналу Р₁ – h₁

 

Рис.5 – переходные процессы по каналу Р₁ – h₂

 

Переходные процессы при возмущении по входу Р₁ оказались монотонными и апериодическими. Значения уровней асимптотически приближаются к соответствующим значениям статических характеристик, вычисленных в предыдущих пунктах:

При Р₁ = 3,6*10⁵ Па (-10%): h₁ = 1,349 (м) и h₂ = 0,899 (м)

При Р₁ = 3,8*10⁵ Па (-5%): h₁ = 1,424 (м) и h₂ = 0,949 (м)

При Р₁ = 4,2*10⁵ Па (+5%): h₁ = 1,574 (м) и h₂ = 1,049 (м)

При Р₁ = 4,4*10⁵ Па (+5%): h₁ = 1,649 (м) и h₂ = 1,099 (м)

 

Теперь построим переходные процессы при возмущении по входу α₂.

Текст MatchCAD аналогичен, поэтому здесь не приводиться.

Переходные процессы по каналу α₂ – h₁ также имеют монотонный характер и большую длительность.

 

При α₂ = 1.414*10^-5 (-10%): h₁ = 1,611 (м) и h₂ = 0,996 (м)

При α₂ = 1.492*10^-5 (-5%): h₁ = 1,551 (м) и h₂ = 0,998 (м)

При α₂ = 1.650*10^-5 (+5%): h₁ = 1,526 (м) и h₂ = 1,000 (м)

При α₂ = 1.728*10^-5 (+10%): h₁ = 1,415 (м) и h₂ = 1,001 (м)

 

Рис.6 – переходные процессы по каналу α₂ – h₁

 

 

Переходные процессы по каналу α₂ – h₂, имеют совершенно другой вид. Они не апериодические и не колебательные. В первые моменты времени происходит резкое, по сравнению с полной длительностью процесса, изменение уровня в прямом направлении, то есть при уменьшении α₂ уровень резко уменьшается, а при увеличении α₂ – резко увеличивается. А затем идет плавный возврат к начальному значению, но не до конца. Уровень принимает новое значение, очень близкое к начальному отличие от начального значения объясняется округлением вычислений при выводе графиков. Установившиеся значения соответствуют статистической характеристике. Объяснить такой график можно тем, что при изменении α₂, расход воды на перетоке Q₁₂ меняется быстрее, чем расход Q₂ на выходе из бака. То есть уровень h₂ сначала меняется за счет перетока Q₁₂, но с ростом уровня этот расход стабилизируется, и большее влияние на уровень начинает оказывать расход воды на выходе из бака Q₂.

 

12	Поделиться:

Воспользуйтесь поиском по сайту: