Модель динамического программирования

Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы (шаги). Такие операции называют многошаговыми.

В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом. Этот принцип и идея включения конкретной задачи оптимизации в семейство аналогичных многошаговых задач приводят к рекуррентным соотношениям – функциональным уравнениям – относительно оптимального значения целевой функции. Их решение позволяет последовательно получить оптимальное управление для исходной задачи оптимизации.

Дадим общее описание модели динамического программирования.

Рассматривается управляемая система, которая под влиянием управления переходит из начального состояния  в конечное состояние . Предположим, что процесс управления системой можно разбить на n шагов. Пусть , ,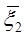…,  - состояния системы после первого, второго,…, n-го шага. Схематически это показано на рис. 1.

Состояние  системы после k-го шага (k=1,2,…,n) характеризуется параметрами 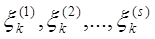, которые называют фазовыми координатами. Состояние  можно изобразить точкой s-мерного пространства, называемого фазовым пространством. Последовательное преобразование системы (по шагам) достигается с помощью некоторых мероприятий 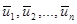, которые составляют управление системой U= ,

где  - управление на k-м шаге, переводящее систему из состояния  в состояние  (рис.1). Управление  на k-м шаге заключается в выборе значений определенных управляющих переменных .

Предполагаем впредь, что состояние системы в конце k-го шага зависит только от предшествующего состояния системы 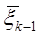 и управления  на данном шаге (рис.1). Такое свойство получило название отсутствия последствия. Обозначим эту зависимость в виде

(1.1)

Равенства (1.1) получили название уравнений состояний. Функции  полагаем заданными.

Варьируя управления U, получим различную «эффективность» процесса, которую будем оценивать количественно целевой функцией Z, зависящей от начального состояния системы  и от выбранного управления U:

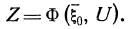(1.2)

Показатель эффективности k-го шага процесса управления, который зависит от состояния  вначале этого шага и управления , выбранного на этом шаге, обозначим через  (рис. 1). В рассматриваемой задаче пошаговой оптимизации целевая функция (1.2) должна быть аддитивной, т.е.

(1.3)

Обычно условиями процесса на управление на каждом шаге  накладываются некоторые ограничения. Управления, удовлетворяющие этим ограничениям, называются допустимыми.

Задачу пошаговой оптимизации можно сформулировать так: определить совокупность допустимых управлений , переводящих систему из начального состояния в конечное состояние  и максимизирующих (минимизирующих) показатель эффективности (1.3).

Для единообразия формулировок (но не вычислительных процедур!) в дальнейшем будем говорить только о задаче максимизации, имея в виду, что если необходимо минимизировать Z, то заменив Z на Z’=-Z перейдем к максимизации Z’.

Начальное состояние и конечное состояние  могут быть заданы однозначно или могут быть указаны множество  начальных состояний и множество конечных состояний так, что . В последнем случае в задаче пошаговой оптимизации требуется определить совокупность допустимых управлений, переводящих систему из начального состояния  в конечное  и максимизирующих целевую функцию (1.3). Управление, при котором достигается максимум целевой функции (1.3) называется оптимальным управлением и обозначается через U*= .

Если переменные управления  принимают дискретные значения, то модель ДП называется дискретной. Если же указанные переменные изменяются непрерывно, то модель ДП называется непрерывной. В зависимости от числа параметров состояний (s) и числа управляющих переменных на каждом шаге (r) различают одномерные и многомерные модели ДП. Число шагов в задаче может быть либо конечным, либо бесконечным.

ДП применяется при оптимизации как детерминированных, так и стохастических процессов.

В некоторых задачах, решаемых методом ДП, процесс управления естественно разбивается на шаги. Например, при распределении на несколько лет ресурсов деятельности предприятия шагом естественно считать временной период; при распределении средств между n предприятиями номером шага естественно шага номер очередного предприятия. В других задачах разбиение на шаги вводится искусственно. Например, непрерывный управляемый процесс можно рассматривать как дискретный, условно разбив его на некоторые временные отрезки – шаги. Исходя из условий каждой конкретной задачи, длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.