 |
Общее описание процесса моделирования и построения вычислительной схемы динамического программирования
|
|
|
|
Общая задача оптимизации, чтобы ее можно было описать моделью ДП должна удовлетворять следующим условиям:
1. Задача может интерпретироваться как n-шаговый процесс управления, а показатель эффективности процесса может быть представлен в аддитивной форме, т.е. как сумма показателей эффективности на каждом шаге.
2. Структура задачи инвариантна относительно числа шагов п, т. е. должна быть определена для любого n и не зависеть от этого числа.
3. На каждом шаге состояние системы определяется конечным числом s параметров состояния и управляется конечным числом r переменных управления, причем s и r не зависят от числа шагов п.
4. Выбор управления на k-м шаге не влияет на предшествующие шаги, а состояние в начале этого шага есть функция только предшествующего состояния и выбранного на нем управления (отсутствие последействия).
Построение модели ДП сводится к следующим основным моментам:
1) выбирают способ деления процесса на шаги;
2) вводят параметры состояния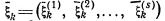 
и переменные управления 
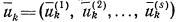на каждом шаге процесса;
3) записывают уравнение состояния
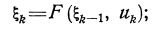(3.1)
4) вводят показатели эффективности на k-м шаге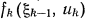 
и суммарный показатель – целевую функцию
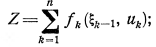(3.2)
5) вводят в рассмотрение условные максимумы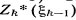 
показателя эффективности от k-гo шага (включительно) до конца процесса и условные оптимальныеуправления на k-м шаге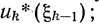 
6) из ограничений задачи определяют для каждого шага множества Dk допустимых управлений на этом шаге;
7) записывают основные для вычислительной схемы ДП функциональные уравнения Беллмана
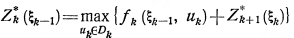(3.3)
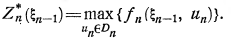(3.4)
Несмотря на единообразие в общем построении модели ДП, приведенном выше, вычислительная схема строится в зависимости от размерности задачи, характера модели (дискретной или непрерывной), вида функций (3.1), (3.2) и других характеристик модели. При всем разнообразии вычислительных схем ДП можно отметить в них некоторые общие черты.
|
|
|
1. Решение уравнений (3.3) проводят последовательно, начиная с (3.4). Этот этап получил название условной оптимизации.
2. В результате последовательного решения п частных задач на условный максимум определяют две последовательности функций: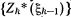 
—условные максимумы и соответствующие им 
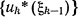—условные оптимальные управления.
3. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях их можно получить аналитически.
4. После выполнения первого этапа (условной оптимизации) приступают ко второму этапу — безусловной оптимизации.
а) Если начальное состояние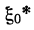 
задано 
,
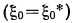то непосредственно определяют максимум целевой
функции
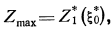(3.5)
а затем — искомое безусловное оптимальное управление по цепочке
(3.6)
В этой цепочке переход, указанный сплошной линией, проводят по последовательности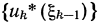 
, а пунктирной — с помощью уравнений состояний.
б) Если задано множество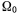 
начальных состояний,
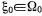, то дополнительно решают еще одну задачу на максимум:
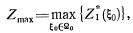(3.7)
откуда находят 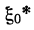, а затем, как и в п. а), по цепочке (3.6) —безусловное оптимальное управление.
Иногда на этапе условной оптимизации вычислительный процесс удобно строить в направлении, обратном описанному выше, т. е. от 1-го шага к л-му. Этот способ получил название прямого хода вычислений в отличие от вышеизложенного, который называется обратным ходом. Уравнения состояний для прямого хода удобно записывать в виде
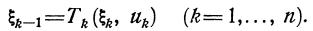(3.8)
Они могут быть получены решением уравнений (1.1) относительно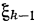 
. Введем в рассмотрение условные максимумы показателя эффективности за k шагов, от 1-го до k-го включительно — величины 
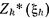. Повторив рассуждения п. 2.2.2., придем к следующей форме уравнений Беллмана:
|
|
|
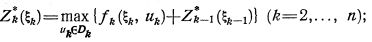(3.9)
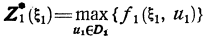(3.10)
В результате решения этих уравнений получим последовательности
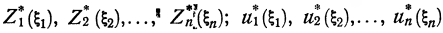(3.11)
Этап безусловной оптимизации не отличается принципиально от аналогичного этапа в обратном ходе вычислений: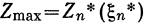 
, если 
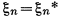задано, или
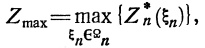(3.12)
если указано множество 
возможных конечных состояний. Далее, определяем безусловное оптимальное управление по цепочке
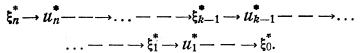(3.13)
|
|
|
