 |
Ряд динамики и методы определения тенденций.
|
|
|
|
Процессы и явления общественной жизни, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении. Статистические данные, характеризующие изменения явлений во времени, называются динамическими (хронологическими или временными) рядами. Такие ряды строят для выявления и изучения складывающихся закономерностей в развитии явлений экономической, политической и культурной жизни общества. [18, с. 87]
При изучении рядов динамики должны быть решены следующие задачи: характеристика интенсивности развития явления от периода к периоду (от даты к дате), характеристика средней интенсивности развития явления за исследуемый период, выявление основной тенденции (тренд) в развитии явления, осуществление прогноза развития на будущее, а также анализ взаимосвязанных рядов динамики и сезонности колебаний.
Для изучения интенсивности изменения уровней ряда во времени исчисляются аналитические показатели [18, с. 89] [12, с. 117], расчет которых представлен в приложении 10.
На основе полученных данных приложения 10 можно сделать вывод о достаточно невысоком росте среднего значения численности занятого населения по регионам Российской Федерации за период с 2000-2007 гг. на 29529 чел. (4,36 %). Однако за весь период с каждым годом наблюдается увеличение среднегодовой численности занятого населения России, то есть прирост среднегодовой численности занятого населения имеет только положительную динамику. Наиболее интенсивное увеличение произошло в 2002 г. по равнению с 2001 г, когда среднегодовая численность занятого населения увеличилась на 0,87%, или на 5904 чел, а также в 2006 г. по сравнению с 2005 г. – на 0,83 %, или на 5752 чел.
Усредненные показатели найдены по формулам:
|
|
|
чел.; 
чел.;
Полученные результаты констатируют, что среднее значение этого показателя за указанный период в среднем каждый год увеличивается на 4218 чел., или 0,61%. Соответственно, и абсолютное значение одного процента прироста численности занятого населения в России в 2000-2007 гг. увеличивалось.
В нашем случае закономерность изменения изучаемого явления, общая тенденция его развития явно и отчетливо отражаются уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут). Однако часто приходится встречаться с такими рядами динамики, в которых уровни ряда претерпевают самые различные изменения (то возрастают, то убывают), и общая тенденция развития неясна.
На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер. Поэтому при анализе динамики речь идет не просто о тенденции развития, а об основной тенденции, достаточно стабильной (устойчивой) на протяжении изученного этапа развития.
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. [12, 124]
При затруднении выбора формы кривой, можно привести расчет наиболее часто используемых моделей для аналитического выравнивания. По полученным моделям для каждого периода (каждой даты) определяются теоретические уровни тренда, стандартная ошибка аппроксимации и коэффициент вариации (см. приложение 11).
На основании ряда динамики среднегодовой численности занятого населения, для выявления общей тенденции использованы наиболее часто применяемые методы: укрупнения периодов, средней скользящей, аналитического выравнивания.
|
|
|
Первые методы не позволяют выявить общую тенденцию (тренд) в данном динамическом ряду, поэтому наиболее прогрессивным методом является метод аналитического выравнивания.
Выявим модель тренда (уравнение прямой) для определения тенденции.
, где а 0 – начальный уровень ряда динамики (свободный член уравнения), а 1 – характеризует средний прирост изучаемого признака в данной динамике.
В нашем случае:
Значит модель тренда (уравнение прямой) для определения тенденции имеет следующий вид: 
.
По данным уравнения видно, что наблюдается среднее увеличение среднегодовой численности занятого населения по годам на 4254 чел.
Ошибка аппроксимации (среднее квадратическое отклонение от тренда) составляет 898 чел.,коэффициент вариации 1,3%:
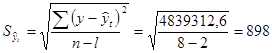чел.; 
чел.
.
Выявим модель тренда (уравнение параболы) для определения тенденции.
, где а 2 – средний абсолютный прирост в единицу времени t.
В нашем случае:
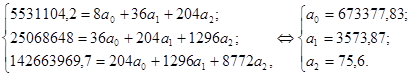
Значит, модель тренда (уравнение параболы) для определения тенденции будет иметь следующий вид: 
. По данным уравнения тренда видно, что в среднем за год среднегодовая численность занятого населения увеличивается на 3574 чел.
Ошибка аппроксимации составляет 881 чел., коэффициент вариации 1,27%:
чел.; 
.
Парабола лучше отражает тенденцию развития явления во времени, т.к. ошибка аппроксимации меньше.
Так как коэффициент вариации не превышает 25%, следовательно данный динамический ряд устойчив и данную модель тренда можно использовать при прогнозировании.
Уравнение тренда применяют при прогнозировании, т.е. определения уровней ряда динамики за его пределами – метод экстраполяции. Прогноз может быть точечным (по уравнению тренда) или интервальным (с использованием ошибки аппроксимации) [21].
При прогнозе следует определить:
- на основании какого числа уровней ряда динамики можно построить уравнение тренда;
- каким может быть горизонт прогнозирования (период упреждения).
Период прогнозирования не должен превышать 1/3 числа уровней, на основе которых построено уравнение тренда.
Точечный прогноз:
Для 2008 г. - 
чел.
Для 2009 г. - 
чел.
Интервальный прогноз осуществляется по формуле:
; 
чел. (найдено выше)
|
|
|
Р = 0,95, k = n – 1 = 8 – 1 = 7, => 
(по таблице значений критерия t Стьюдента, приложение 12). [17, с. 382]
Интервальный прогноз:
Для 2008 г.: 
,
Для 2009 г.: 
Значит с вероятностью 95 % можно утверждать, что среднее значение численности занятого населения по регионам России в 2008 г. будет составлять в пределах от 709583 до 713749 чел. А в 2009 г. – от 714593 до 718760 чел.
Прогнозирование среднегодовой численности занятого населения можно производить также при помощи полиномиальной функции различных порядков, экспоненциальной функции, логарифмической и степенной функции (Приложения 13,14,15).
Строится график зависимости между временным периодом и среднегодовой численностью занятого населения, проводится линия тренда и на ее основании составляется прогноз.
Как видно из приводимых на графиках формул и величины достоверности аппроксимации наиболее значимым является прогноз по полиномиальной функции 3-го порядка. Тем не менее, такая функция дает достаточно достоверные результаты только при большом количестве периодов (не менее 5 периодов на каждый уровень полиномиальной функции).
Индексный метод анализа.
Если численность занятого населения (S) рассматривается во взаимосвязи с численностью населения в трудоспособном возрасте (T) (приложение 16), уровнем занятости трудовых ресурсов (y) (приложение 17) и приминает форму не простого, взятого изолированного показателя S, а составного S = Т · y, то при сопоставлении его уровней используют индексный метод. Индексы позволяют определить влияние факторов на изменение численности занятого населения. [12, с. 145]
По Российской Федерации, численность населения которой поддается суммированию, определяется агрегатный индекс численности занятого населения:
или 104,36 %.
чел.
Поскольку изменение численности занятого населения, как и любого абсолютного результативного показателя, зависит от изменения числа единиц совокупности – носителей изучаемого признака (численность населения в трудоспособном возрасте Т), значений признака (уровень занятости трудовых ресурсов у) и структуры совокупности (т.е. соотношения единиц с разным значением признака), - то агрегатный индекс в процессе анализа разлагается на индексы численности населения в трудоспособном возрасте I Т, уровня занятости трудовых ресурсов I y и структуры численности населения в трудоспособном возрасте I стр. [17, c. 104]. Практически используются две идентичные по результатам схемы разложения общего индекса:
|
|
|
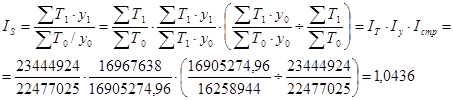
что составляет 104,36 %.
где 
= 
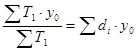- условный средний уровень занятости трудовых ресурсов при отчетной структуре численности населения в трудоспособном возрасте и базисном уровне занятости трудовых ресурсов.
Разложение индексов можно видеть на примере анализа динамики среднегодовой численности занятого населения по регионам России за 2007 г. (отчетный год) по сравнению с 2000 г. (базисный год), изображенном в таблице 2.6.1.
Таблица 2.6.1
|
|
|
