Тема 3. Действительные числа и их множества

Множество всех действительных чисел и множество всех точек числовой прямой, эквивалентность этих множеств. Свойства действительных чисел. Свойство непрерывности. Множество действительных чисел (точечное множество на числовой прямой). Понятия e – окрестности действительного числа (точки), e – окрестности с выколотым центром. Понятия внутренней точки точечного множества на числовой прямой и открытого множества. Понятия граничной точки точечного множества на числовой прямой, границы и замкнутого множества. Взаимосвязь между открытыми и замкнутыми множествами на числовой прямой. Понятия предельной и изолированной точки точечного множества на числовой прямой. Производное множество, замыкание множества. Множества плотные в себе, совершенные и замкнутые. Множество мажорант и минорант множества действительных чисел. Ограниченные (сверху, снизу) и неограниченные (сверху, снизу) множества. Наибольший (наименьший) элемент множества. Верхняя (нижняя) грань множества. Рабочее определение верхней (нижней) грани. Теорема о существовании верхней (нижней) грани множества, ограниченного сверху (снизу).

Тема 4. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

Понятие функции натурального аргумента (числовой последовательности), предела последовательности. Единственность предела последовательности. Примеры сходящихся и расходящихся последовательностей. Понятие бесконечно малой последовательности. Связь понятий предела и бесконечно малой. Бесконечно большие последовательности, их связь с бесконечно малыми. Теорема о сравнении бесконечно малых последовательностей. Теорема о сумме бесконечно малых последовательностей. Понятие ограниченной последовательности. Ограниченность сходящейся последовательности. Теорема о произведении бесконечно малой последовательности на ограниченную, следствия из нее. Лемма об устойчивости знака (слабый и сильный варианты). Пределы последовательностей 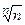, , . Теорема о пределе суммы, произведения, отношения двух последовательностей. Теоремы о переходе к пределу в неравенствах.

Теорема Вейерштрасса о сходимости монотонной ограниченной последовательности. Примеры применения, доказательство сходимости последовательности . Понятие о числе «е». Лемма о стягивающихся отрезках. Понятие предельной точки (частичного предела) последовательности. Лемма о предельной точке и теорема Больцано-Вейерштрасса об ограниченной последовательности. Понятие фундаментальной последовательности. Критерий Коши сходимости последовательности.

Тема 5. ПРЕДЕЛ ФУНКЦИИ

Понятие предела функции. Конечный и бесконечный предел функции одной переменной (по Коши, по Гейне, односторонние и двусторонние пределы). Различные варианты пределов. Единственность предела. Бесконечно большие функции. Бесконечно малые функции. Связь понятий предела и бесконечно малой. Связь между бесконечно малыми и бесконечно большими функциями. Теорема сравнения бесконечно малых. Теорема о сумме бесконечно малых функций. Ограниченные функции, локально ограниченные функции. Локальная ограниченность функции, имеющей предел. Теорема о произведении бесконечно малой функции на локально ограниченную. Следствия из нее. Лемма об устойчивости знака функции (слабый и сильный варианты). Предел суммы, произведения, отношения двух функций. Теоремы о переходе к пределу в неравенствах. Теорема “о двух милиционерах”. Теоремы о предельном переходе в сложной функции. Первый замечательный предел. Второй замечательный предел.

Эквивалентные функции. Теорема о замене функций на эквивалентные в произведении и отношении (при вычислении пределов). Символ о -малое, его свойства. Необходимое и достаточное условие эквивалентности двух функций. Использование символа о -малое при вычислении пределов. Понятие о правиле Лопиталя вычисления пределов. Понятие о формуле Маклорена, формулы Маклорена для основных элементарных функций, их использование при вычислении пределов. Понятие асимптоты. Определение параметров наклонной асимптоты.