 |
Принятие решения приемником по одному отсчету
|
|
|
|
Сообщения передаются последовательностью двоичных символов “1” и “0”, которые появляются с априорными вероятностями соответственно  и
и  . Этим символам соответствуют канальные сигналы
. Этим символам соответствуют канальные сигналы  и
и  , которые точно известны в месте приема.
, которые точно известны в месте приема.
В канале связи на передаваемые сигналы воздействует гауссовский стационарный шум с дисперсией  . Приемник, оптимальный по критерию идеального наблюдателя (минимума средней вероятности ошибки), принимает решение по одному отсчету смеси сигнала и помехи:
. Приемник, оптимальный по критерию идеального наблюдателя (минимума средней вероятности ошибки), принимает решение по одному отсчету смеси сигнала и помехи:

на интервале элемента сигнала длительности  . Амплитуда канальных сигналов
. Амплитуда канальных сигналов  .
.
Отношением правдоподобия называется величина, определяемая выражением:
 ,
,
где  - плотность вероятности того, что принятый сигнал
- плотность вероятности того, что принятый сигнал  образовался при передачи сигнала
образовался при передачи сигнала  .
.
Таким образом, отношение правдоподобия (применительно к задаче) есть величина, равная отношению плотности вероятности того, что принятый сигнал  образовался при передаче символа “1”, к плотности вероятности того, что принятый сигнал образовался при передаче символа “0”.
образовался при передаче символа “1”, к плотности вероятности того, что принятый сигнал образовался при передаче символа “0”.
Свою очередь, выражение, стоящее справа:
 ,
,
где  ,
,  - априорные вероятности,
- априорные вероятности,
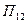 ,
,  - весовые коэффициенты.
- весовые коэффициенты.
называется пороговым отношением правдоподобия.
Приемник, использующий отношение правдоподобия, работает следующим образом.
1. Анализируя поступающий на его вход сигнал, вычисляет отношение правдоподобия  .
.
2. По известным значениям  и
и  , а также заданным
, а также заданным  и
и 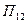 , вычисляется пороговое отношение правдоподобия
, вычисляется пороговое отношение правдоподобия  .
.
3. Величина  сравнивается с
сравнивается с  , если
, если  >
>  , приемник выдает сигнал
, приемник выдает сигнал 
 , в противном случае сигнал
, в противном случае сигнал  .
.
Согласно критерию идеального наблюдателя, весовые коэффициенты  . Тогда пороговое отношение правдоподобия принимает вид:
. Тогда пороговое отношение правдоподобия принимает вид:
|
|
|

Критерий идеального наблюдателя широко применяется в системах связи, когда искажения любого сигнала одинаково нежелательны.
Плотность распределения огибающей суммы сигнала и помехи определяется обобщенным законом Релея (Релея-Райса):
 - передача «1»,
- передача «1»,
где  - модифицированная функция Бесселя.
- модифицированная функция Бесселя.
Плотность распределения огибающей помехи определяется простым законом Релея:
 - передача «0».
- передача «0».
Плотность распределения в точке  :
:


Отношение правдоподобия:

Пороговое отношение правдоподобия:

Т.к.  (0,0957<0,11), то приемник примет решение в пользу сигнала
(0,0957<0,11), то приемник примет решение в пользу сигнала  , т.е. примет «0».
, т.е. примет «0».
Составим таблицу для построения графиков кривых плотностей распределения.
Т.к. передача символа «0» соответствует паузе, то в этот момент в канале присутствует только помеха (мощность сигнала в  паузе равна нулю), а, следовательно, плотности распределения огибающей помехи
паузе равна нулю), а, следовательно, плотности распределения огибающей помехи  и огибающей сигнала+помеха при передаче «0»
и огибающей сигнала+помеха при передаче «0»  будут совпадать.
будут совпадать.
Таблица 1 – Расчет кривых плотностей распределения  и условных вероятностей
и условных вероятностей  и
и 
| z, мВ | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | 2 | 3 |
| z, В | 0 | 0,0002 | 0,0004 | 0,0006 | 0,0008 | 0,001 | 0,002 | 0,003 |
| W(z/1) | 0 | 0,952925 | 1,921554 | 2,921497 | 3,968173 | 5,076711 | 12,04255 | 22,45071 |
| W(z/0) | 0 | 15,4083 | 30,67426 | 45,65774 | 60,2229 | 74,24032 | 132,2526 | 163,576 |
| 3,6 | 4 | 5 | 6 | 7 | 8 | 8,5 | 9 | 10 |
| 0,0036 | 0,004 | 0,005 | 0,006 | 0,007 | 0,008 | 0,0085 | 0,009 | 0,01 |
| 30,72502 | 37,09789 | 55,57029 | 75,97625 | 95,13917 | 109,3685 | 113,6224 | 115,6129 | 112,524 |
| 168,4807 | 166,4838 | 147,0569 | 115,4408 | 81,56218 | 52,25802 | 40,38793 | 30,51176 | 16,28832 |
| 11 | 12 | 13 | 14 | 15 | 16 | |||
| 0,011 | 0,012 | 0,013 | 0,014 | 0,015 | 0,016 | |||
| 100,93 | 83,49256 | 63,73451 | 44,91554 | 29,23286 | 17,5763 | |||
| 7,969111 | 3,579556 | 1,478126 | 0,561702 | 0,196593 | 0,063414 |

Рис. 5 – Графики распределения плотности вероятностей
 4 Вероятность ошибки на выходе приемника
4 Вероятность ошибки на выходе приемника
Вероятность неправильного приема двоичного символа в приемнике ДАМ нкг определяется как:
 ,
,
где  - отношение сигнал/шум,
- отношение сигнал/шум,
 - табулированный интеграл вероятностей.
- табулированный интеграл вероятностей.
|
|
|
Т.к.  , то вероятность неправильного приема считается равной:
, то вероятность неправильного приема считается равной:
 .
.
Следовательно, 
Реальная полоса пропускания приемника составляет:
 (расчет приведен в Приложении)
(расчет приведен в Приложении)
Построим зависимость  .
.
Таблица 2 – Расчет графика зависимости 
| h | 0 | 0,5 | 1 | 1,5 | 2 | 3 |
| P | 0,5 | 0,469707 | 0,3894 | 0,284891 | 0,18394 | 0,0527 |
| 4 | 5 | 6 | 7 | 8 | 9 |
|
| 0,009158 | 0,000965 | 6,17E-05 | 2,39E-06 | 5,63E-08 | 8,03E-10 |
|

Рис. 6 – График зависимости 
|
|
|


