Интерференция в тонких пластинках. Линии равной толщины и равного наклона. Кольца Ньютона.

Интерференция в тонких пластинках. Каждому неоднократно приходилось наблюдать радужную окраску мыльных пленок, тонких пленок нефти или минерального масла, плавающих на поверхности воды, цвета побежалости на поверхности закаленных стальных деталей, покрытых тончайшим прозрачным слоем окислов. Все эти явления обусловлены интерференцией света в тонких прозрачных пленках, которая возникает в результате наложения когерентных волн, отражающихся от верхней и нижней поверхностей пленки.

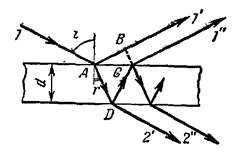Для установления общих закономерностей интерференции света в тонких пленках рассмотрим плоскопараллельную прозрачную пленку толщиной d, на которую падает под углом i плоская монохроматическая волна (луч 1). Будем предполагать, что по обе стороны от пленки находится одна и та же среда (например, воздух). Абсолютные показатели преломления этой среды и пленки обозначим через n₁ и n₂, причем для определенности будем считать, что n­₂ > n₁.

Падающая волна частично отражается от верхней поверхности пленки (луч 1'), а частично преломляется (луч AD). Преломленная волна, достигнув нижней поверхности пленки, также частично отражается (луч DC), а частично преломляется (луч 2'). То же самое вновь происходит на верхней поверхности пленки с волной, распространяющейся вдоль луча DC, причем преломленная волна (луч 1") накладывается на волну, непосредственно отраженную от верхней поверхности (луч 1'). Эти две волны когерентны. Результат их интерференции зависит от разности фаз ∆Ф колебаний, возбуждаемых этими волнами соответственно в точках С и В плоскости ВС, проведенной перпендикулярно лучам 1' и 1". Колебания, вызываемые в точке С волной, отраженной от нижней поверхности пленки, отстают по фазе от колебаний в точке А на величину ∆Ф₁ = 2π(|AD| + |DC|)/λ₂, где λ₂ — длина волны света во второй среде (при прохождении волной расстояния, равного λ, ее фаза изменяется на 2π). Аналогично этому, отставание по фазе колебаний в точке В, вызываемых волной, которая отражается от верхней поверхности пленки, равно ∆Ф₂ = 2π|AB|/λ₁ + π, где λ₁ — длина волны света в первой среде. Добавочный член π учитывает сдвиг фаз, возникающий при отражении света от оптически более плотной среды (мы полагали, что n­₂ > n1; если бы n­₂ было меньше n­₁, то добавочный член π нужно было бы ввести в выражение для ∆Ф₁, а не для ∆Ф₂). Сдвиг по фазе на π, при отражении, эквивалентен дополнительному пути света в первой среде, равному λ₁/2. Таким образом, искомая разность фаз интерферирующих волн

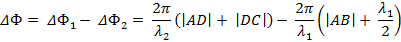
Длины волн λ₂ и λ₁ связаны с длиной волны λ света той же частоты ν, распространяющегося в вакууме, следующими соотношениями

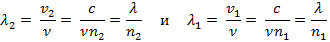
где v₁ и v₂ – фазовые скорости света в обеих средах.

Т.о.,

(1)

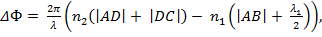
или

 

 

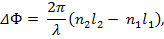
где l₂ = |AD| + |DC| и l₁ = |AB| + λ₁/2 – геометрические длины путей, пройденных интерферирующими волнами во второй и первой средах (с учетом возможных потерь полуволны при отражении). Произведение геометрической длины пути l световой волны в среде на абсолютный показатель преломления n последней называется оптической длиной пути s: s = nl. Из формулы (1) следует, что

 

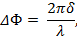
где δ = s₂ – s₁ = n₂l₂ – n₁l₁ — оптическая разность хода интерферирующих волн.

Интерференция наблюдается не только в отраженном, но и в проходящем сквозь пленку свете. Можно легко показать (предоставляем это сделать читателю), что оптическая разность хода для проходящего света отличается от δ для отраженного света на λ/2. Следовательно, максимумам интерференции в отраженном свете соответствуют минимумы интерференции в проходящем свете, и наоборот. Поэтому при освещении пленки белым светом ее окраска в отраженном и проходящем свете оказывается взаимно дополнительной.

Линии равной толщины и равного наклона. При освещении плоскопараллельной пленки монохроматическим светом результаты интерференции отраженного света в различных точках экрана Э зависят только от углов i падения на пленку или равных им углов отражения для лучей, собирающихся в этих точках экрана. Интерференционная картина имеет вид чередующихся криволинейных темных и светлых полос. Каждой из этих полос соответствует определенное значение угла i. Поэтому они называются полосами или линиями равного наклона. При освещении пленки белым светом на экране наблюдается система разноцветных полос равного наклона. Легко видеть, что в том случае, когда оптическая ось линзы Л перпендикулярна поверхности пленки, полосы равного наклона должны иметь вид концентрических колец с центром в главном фокусе F линзы. Это явление используется на практике для весьма точного контроля степени плоскопараллельности тонких прозрачных пластинок (например, стеклянных): изменение толщины пластинки на величину порядка 10 нм (10^-8 м) уже можно обнаружить по искажению формы колец равного наклона.

В отсутствие линзы параллельные лучи 1' и 1", 2' и 2" и т. д. «пересекаются» только в бесконечности. Поэтому часто говорят, что полосы равного наклона локализованы в бесконечности. Их можно непосредственно наблюдать глазом, если последний аккомодирован на бесконечность, т. е. фокусирует на сетчатке поступающие в него параллельные лучи света образующие всевозможные углы с оптической осью глаза.

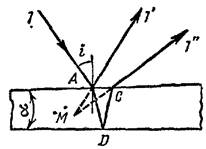Рассмотрим теперь еще один возможный случай — интерференцию света в тонких пленках, толщина которых не одинакова в разных местах. На рисунке изображена простейшая пленка такого типа, имеющая форму плоского клина с малым углом а между боковыми гранями. Пусть на клин падает плоская волна, направление распространения которой совпадает с лучом 1. Направления распространения интерферирующих волн, возникающих в результате отражения света от верхней и нижней поверхностей клина, показаны соответственно лучами 1' и 1". Оптическая разность хода между ними выражается формулами:

 

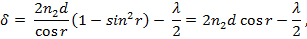
или

 

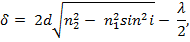
где d— средняя толщина клина на участке АС. Поскольку значения i, n₂ и n₁ постоянны, одинаковым значениям d соответствуют одинаковые оптические разности хода, а следовательно, и одинаковые результаты интерференции. Поэтому в отраженном свете должны наблюдаться интерференционные полосы (линии) равной толщины.

Верхняя и нижняя грани клина не параллельны между собой, так что лучи 1’ и 1” имеют несколько различные направления. Для наблюдателя, смотрящего навстречу этим лучам, они кажутся выходящими из точки М, расположенной вблизи поверхности клина. Поэтому говорят, что полосы ровной толщины локализованы вблизи поверхности тонкой пленк и, в которой они наблюдаются.

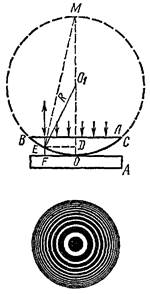Кольца Ньютона. Частным случаем полос равной толщины являются кольца Ньютона. Плосковыпуклая линза Л с большим радиусом R кривизны выпуклой поверхности обращена этой поверхностью к плоской пластине А и соприкасается с ней в точке О. Параллельный пучок света падает нормально на плоскую поверхность ВС линзы и частично отражается от верхней и нижней поверхностей воздушного промежутка между линзой и пластиной. При наложении отраженных волн возникают интерференционные кольца равной толщины. Вид этих колец в случае монохроматического света показан на рисунке внизу. В центре находится темное пятно (минимум нулевого порядка). Оно окружено системой чередующихся светлых и темных колец, ширина и интенсивность которых постепенно убывают по мере удаления от центрального пятна. В проходящем свете наблюдается дополнительная картина — центральное пятно светлое, следующее кольцо темное и т. д.

Оптическая разность хода между лучами, отраженными от верхней и нижней поверхностей воздушного зазора на произвольном расстоянии r = |DE| от точки О, равна

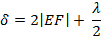
где показатель преломления воздуха принят равным единице, а член λ/2 обусловлен сдвигом по фазе на π при отражении света от поверхности пластины. Из подобия прямоугольных треугольников ⊿EOD и ⊿EDM следует, что

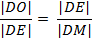
где |DO| = |EF|, |DE| = r и |DM| = 2R - |EF| ≈ 2R, т.к. 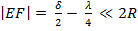. Таким образом,

 

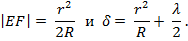
Из этого соотношения следует, что радиусы k -х светлого () и темного (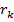) колец Ньютона в отраженном свете равны:

 

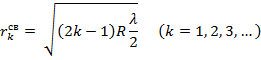
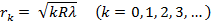
Очевидно, что в проходящем свете

 

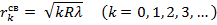
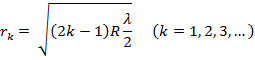
Правильная форма колец Ньютона легко искажается при всяких, даже незначительных, дефектах в обработке выпуклой поверхности линзы и верхней поверхности пластины. Поэтому наблюдение формы колец Ньютона позволяет осуществлять быстрый и весьма точный контроль качества шлифовки плоских пластин и линз, а также близость поверхностей последних к сферической форме.

 

12345Следующая ⇒

Поделиться: Я.Мессенджер ВКонтакте Одноклассники Telegram Twitter Мой Мир

Воспользуйтесь поиском по сайту: