Главная | Обратная связь | Поможем написать вашу работу!

Задание к лабораторной работе.

1. Изучить возможности языка Паскаль для организации линейных алгоритмов.

2. Разработать алгоритм, описать его в виде блок-схемы и составить программу для решения задачи соответствующего варианта.

3. Набрать текст программы и отладить ее работу в среде Турбо Паскаль.

4. Подобрать тестовые данные. Протестировать.

5. Оформить отчет о выполнении (см. Приложение 1)

Пример выполнения вычислительных операций

Задание. Вычислить значения p = lg(a+x²)+sin²(z/a), t = x^a и

при a=0,59; z= -4,8; x=2,1

Текст программы

Program lab_2;

Uses crt;

Const a=0.59; z=-4.8; x=2.1;

Var y, p, c, t: real;

Begin

Clrscr;

c:=ArcTan(a+x*x);

y:=Exp(3*Ln(c))+Sqrt(z*z/(a*a+x*x));

p:=(Ln(a+x*x))/Ln(10)+Sqr(Sin(z/a));

t:=Exp(a*Ln(x));

Writeln('При a=', a: 4:2, ' z=', z:4:1,

' x=', x: 3:1);

Writeln ('p=', p:9:4,' y=', y:9:4,

' t=', t: 9:4);

Readln

End.

Результаты вычислений:

При a=0.59 z =-4.8 x =2.1

p =1.6217 у = 4.7911 t =1.5492

Варианты заданий

Таблица 2.1

№ варианта	Расчетная формула	x	y	z

			3,017	-2,69
		2,7	1,83	-0,789
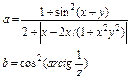
				70⁰
		15,3	81⁰	8,91
		-1	0,59	5,17
Продолжение таблицы 2.1

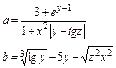
		35⁰	0,95	-1,05
		2,5	5,8	33⁰
		1,5	7⁰
		0,5	15⁰	1,95
		5⁰	1,3	-0,5
		41⁰	10,18	3,72
			2,1	41⁰
Продолжение таблицы 2.1

		8⁰	5,2	2,8
		2,5	5,8	33⁰
		18⁰	4⁰	3,5
			4,021	-5,72
		4,6	2,67	-1,123
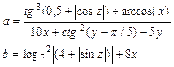
		0,1		63⁰
		21,5	75⁰	7,56
		-2	0,61	4,12
Продолжение таблицы 2.1

		40⁰	2,35	-3,48
		4,05	3,1	40⁰
		2,6	11⁰
		1,5	20⁰	3,06
		15⁰	2,1	-0,78
		31⁰	21,67	5,18
			4,51	51⁰
		18⁰	7,3	3,5
Окончание таблицы 2.1

		3,2	5,8	41⁰
		23⁰	70⁰	8,3

Контрольные вопросы

1. Понятие алгоритма, виды алгоритмов и способы его описания.

2. Общая структура программы на языке Паскаль.

3. Перечислите основные операции и стандартные функции, определенные для данных целочисленного типа. Каков тип результата, возвращаемого каждой функцией?

4. Для представления какой информации в языке Паскаль используется тип real? В чем отличие двух типов числовых данных real и integer?

5. Какие две формы записи вещественных чисел используются в языке Паскаль?

6. Какие стандартные функции для работы с числовыми данными, реализованные в языке Паскаль, вы знаете? Каков тип аргумента и результата, возвращаемого каждой функцией?

7. Перечислите известные Вам стандартные функции преобразования типов.

8. Понятие, назначение и правило записи идентификатора.

9. Что такое «выражение», «операция», «операнд»? Приведите примеры.

10. Приведите примеры вывода вещественного значения в форме с фиксированной и плавающей точкой.

11. Назначение процедур write и writeln.

12. Назначение процедур read и readln.

ЛАБОРАТОРНАЯ РАБОТА №3
Программирование алгоритмов разветвляющейся структуры

Цель работы: получение навыков разработки алгоритмов разветвляющейся структуры, их кодирования, отладки и тестирования.

Задание к лабораторной работе

1. Изучить возможности языка Паскаль для организации алгоритмов ветвления.

3. Набрать текст программы и отладить ее работу в среде Турбо Паскаль.

4. Подобрать тестовые данные. Протестировать.

5. Оформить отчет о выполнении (см. Приложение 1)

Варианты заданий

1. Если три данных числа являются длинами сторон прямоугольного треугольника, то вычислить его площадь и периметр.

2. Если три данных числа могут являться сторонами остроугольного треугольника, то найти его площадь и наименьший острый угол.

3. Если три данных числа могут являться сторонами тупоугольного треугольника, то найти его площадь и тупой угол.

4. Если три данных числа могут являться сторонами равностороннего треугольника, то найти его площадь по формуле Герона.

5. Зная значения длин сторон треугольника, определить его вид (разносторонний, равнобедренный, равносторонний), найти углы такого треугольника.

6. Даны координаты трех точек, если они являются координатами вершин треугольника, то вычислить периметр этого треугольника.

7. Если три данных числа могут являться сторонами разностороннего треугольника, то найти его площадь и высоты.

8. Квадратное уравнение определено его коэффициентами a, b, c. Найти действительные корни заданного уравнения. Если действительных корней нет, то выдать соответствующее сообщение.

9. Даны координаты вершин треугольника, определить его вид (прямоугольный, остроугольный, тупоугольный). Вывести значения его сторон по неубыванию.

10. Прямая задана уравнением y=kx+b, найти количество общих точек этой прямой и окружности x²+y²=r².

11. Известны координаты четырех точек. Выяснить, образуют ли они равнобедренную трапецию, и найти площадь этой трапеции.

12. Дана кривая, заданная уравнением y=x²+c и прямая y=kx+b. Определить, сколько общих точек имеют эти прямые, и найти их координаты.

13. Дана кривая, заданная уравнением y=x²+c и известна длина отрезка. Определить, можно ли данным отрезком соединить точки, координаты которых являются корнями кривой.

14. Даны четыре целых числа. Определить, можно ли из них составить такую квадратную матрицу, чтобы суммы элементов строк были равными и суммы элементов столбцов были равными и вывести эту матрицу.

15. Дано натуральное трехзначное число. Определить является ли оно числом- палиндромом, т.е. одинаково читается при записи справа налево и наоборот.

16. Известны координаты вершин треугольника. Определить, где находится начало координат (внутри треугольника, снаружи или находится на одной из его сторон).

17. Дано натуральное трехзначное число. Определить, упорядочены ли цифры в записи этого числа по неубыванию или по невозрастанию.

18. Даны координаты четырех точек. Определить, можно ли через точки, разделенные попарно, провести параллельные прямые. Если нет, то вывести координаты точки их пересечения.

19. Даны координаты вершин треугольника и окружность, заданная уравнением x ²+ y ²= r ². Определить, является ли окружность вписанной или описанной по отношению к треугольнику.

20. Вычислить значение выражения при заданных значениях x, y, z:

21. Дано вещественное число в форме с фиксированной точкой, содержащее в целой и дробной части по две цифры. Верно ли, что сумма цифр целой части больше суммы цифр дробной части.

22. Дано натуральное трехзначное число. В записи этого числа найти максимальную цифру и записать ее в старший разряд числа.

23. Дано вещественное число в форме с фиксированной точкой. Определить наибольшую цифру среди первых трех цифр дробной части числа.

24. Дано натуральное трехзначное число. Определить количество одинаковых цифр в записи этого числа.

25. Даны координаты вершин треугольника. Если треугольник прямоугольный, вычислить его периметр, в противном случае вычислите его площадь.

26. Задано натуральное трехзначное число. Если в записи этого числа все цифры четные, то найти их сумму, и вычислить их произведение, если это не так.

27. Даны три целых отрицательных числа. Перемножить их попарно и полученные три положительных числа вывести в порядке возрастания.

28. Дано целое четырехзначное число. Проверить, что все четыре цифры числа различны.

29. Известно что из четырех чисел а₁, а₂, а₃, а₄ одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n, и вывести это число, если при умножении на n оно увеличивается не более чем в три раза.

30. Вычислить значение выражения при заданных значениях x, y, z:

ЛАБОРАТОРНАЯ РАБОТА №4
Программирование алгоритмов циклической структуры

Цель работы: получение навыков разработки алгоритмов циклической структуры, их кодирования, отладки и тестирования.

⇐ Предыдущая 123 4 5 6 Следующая ⇒

Воспользуйтесь поиском по сайту: