 |
Сформулируйте понятие несмещенной, состоятельной и эффективной оценки параметра генерального распределения. Приведите примеры.
|
|
|
|
Предположим, что функция распределения генеральной совокупности имеет вид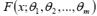 
где 
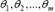неизвестные параметры. Функцию 
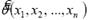, которая при фиксированных значениях 
принимает значение, рассматриваемое как приближенное зна-чение неизвестного параметра θ генерального распределения, называют статистической оценкой па-раметра θ. По определению оценка является несмещенной, если ее математическое ожидание равно оцениваемому параметру. Эффективной называют оценку, которая при заданном объеме выборки п 
имеет наименьшую возможную дисперсию. Наконец, оценка называется состоятельной, если при она стремится (по вероятности) к оцениваемому параметру.
Выборочное среднее
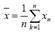
является состоятельной и несмещенной оценкой для генерального среднего. Выборочная дисперсия
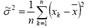
является состоятельной, но смещенной оценкой дисперсии. Статистическая оценка
называемая исправленной дисперсией, является состоятельной несмещенной оценкой генеральной дисперсии.
120.Докажите, что для генерального распределения с математическим ожиданием m и конечной дисперсией σ2 выборочное среднее является несмещенной и состоятельной оценкой m.
Выборочное среднее ¯ x=1/n*Σxn является несмещённой состоятельной оценкой математического ожидания m. Док-во. Поскольку каждая из величин генеральной выборки имеет математическое ожидание M(X), математическое ожидание выборочного среднего ¯ M(X)= 1/n*Σ M(Xi) = M(X), т.е выборочное среднее является несмещённой оценкой. В силу независимости величин выборки D ¯ x=1/n2*ΣD(Xi)=D(x)/n. Состоятельность докажем с помощью нер-ва Чебышева для выборочного среднего с учётом несмещённости: ρ(׀ ¯ x - M(X)׀>= ε) <= D(¯ x) / ε2 = D(x)/n ε2 для всякого ε>0. Поэтому limn→∞ ρ(׀ ¯ x - M(X)׀>= ε)=0. Отсюда limn→∞ ρ(׀ ¯ x - M(X)׀< ε)= 1 - limn→∞ ρ(׀ ¯ x - M(X)׀>= ε) = 1.
|
|
|
121. Пусть X1,…Xn – выборка из распр с дисперсией s2. Док-те, что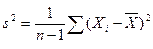 
- несмещенная оценка s2.
Пусть Zn = (x1…xn) – случ выборка объема n, тогда исправленной выборочной дисперсией называется величина s2=n/(n-1) 
. Следствие: S2 – несмещенная оценка s2.
M(S2)=M(n/(n-1)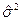 
) = n/(n-1) M(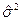) = n/(n-1) * (n-1)/n * s2 = s2, т.к.
M()=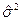 
.
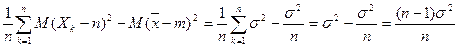Выведите формулу для дисперсии выборочного среднего бесповторной выборки.
В случае простой бесповторной выборки x1…xn мат ожидание и дисперсия выборочного среднего опр по формулам M(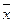
)=m D(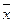)=s2/n * (N-n)/(N-1).
Док-во: 1) M(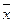) = M ((x1+…+xn)/n) = 1/n (m+…+m)=m.
2)D((x1+…+xn)/n)=1/n2 * D(x1+…+xn) = 1/n2 * {D(x1)+...+D(xn) + 2 
} = 1/n2 (ns2+2C2n*C)=
= 1/n2 (ns2+2*{n(n-1)/2}*C)=1/n (s2+(n-1)C) ====
Рассм. случ выборку, сост из элементов ген совокупности (n=N), тогда 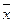- не случ величина, а константа, сл-но, при n=N D(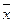)=0=1/N (s2+(N-1)C), сл-но, C = -s2/(N-1)
==== 1/n (s2+(n-1)* {-s2/(N-1)}) = …
Что такое интервальная оценка для параметра q при доверительной вероятности g? Какой практический смысл имеет такая оценка, если g близка к 1? Как изменится доверительный интервал при уменьшении доверительной вероятности?
Пусть q - неизвест пар-р или числовая хар-ка ген распр. Если выполняется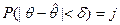 
, то интервал 
- называется доверительным интервалом, который покрывает неизвестный пар-р q ген распределения с доверительной вероятностью g (надежность оценки); d - точность оценки.
Если g близка к 1, то такая оценка является надежной. При уменьшении g, d тоже уменьшается, значит, чтобы точно попасть в интервал его надо развинуть.
124. Пусть n X, X,..., X 1 2 – выборка из нормального распределения с математическим ожиданием m и дисперсией σ 2. Докажите, что для t > 0 интервал накрывает m с вероятностью 2 Ф (t), где Ф (t) – функция Лапласа.
Пусть X1,..., Хn – выборка из нормального распределения Х с параметрами:
M(X)=m, D(X)=σ2
|
|
|
тогда для t>0 доверит. интерв. (X-tσ/√n; X+tσ/√n), где 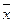– выб. сред., а t – реш-е ур-ния Ф(t) = j/2, к-рый накрывает неизв. параметр m c над-тью j с вер-тью 2Ф(t), т.е. 2Ф(t)=j
Док-во:
Связь между надежностью j и точностью оценки σ. По данному j найдем σ, так чтобы P( 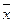-m<σ)=J
X~N(m, σ2), 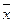~N(m, σ2/n)
P( 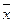-m<σ)=P(m-σ< 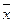<m+σ)=Ф(σ/√ σ2/n)-Ф(σ/ √σ2/n)=2Ф(σ√n/ σ)=j, где σ√n/ σ=t => 2Ф(t)=λ
126 Укажите приближенный γ -доверительный интервал для доли признака в генеральной совокупности по относительной частоте. При каких n формула дает хорошее приближение?
Пусть р - доля признака генеральной совокупности, k/n-выборочная доля, тогда доверительный интервал равен:
Где Ф(t)=γ/2
n≥50
|
|
|
