 |
Анализ модели АСР после модернизации
|
|
|
|
2.8.1 Выбор типа регулятора
Необходимым условием надежной устойчивой работы АСР является правильный выбор типа регулятора и его настроек, гарантирующий требуемое качество регулирования.
В зависимости от свойств объектов управления, определяемых его передаточной функцией и параметрами, и предполагаемого вида переходного процесса выбирается тип и настройка линейных регуляторов[20].
Основные области применения линейных регуляторов определяются с учетом следующих рекомендаций:
И – регулятор со статическим ОР – при медленных изменениях возмущений и малом времени запаздывания (τ/Т <0.1);
П – регулятор со статическим и астатическим ОР – при любой инерционности и времени запаздывания, определяемом соотношением τ/Т <0.1;
ПИ – регулятор – при любой инерционности и времени запаздывания ОР, определяемом соотношением τ/Т <1;
ПИД – регуляторы при условии τ/Т <1 и малой колебательности исходных процессов.
Для того, чтобы правильно выбрать необходимый тип вносимого в систему регулятора, исследуем переходный процесс объекта управления на основании передаточной функции W(p) установки БДР-25/2 полученной в ходе идентификации ТОУ. Построим функциональную схему в SIMULINK (рис. 2.18) и с помощью LAT (Linear Analysis Tool) получим переходную характеристику системы до модернизации на (рис. 2.19).

Рисунок 2.18 - Схема моделирования АСР после модернизации в Simulink
Рисунок 2.19 - Переходная характеристика системы после модернизации
В поле графика (рис. 2.19) указаны основные характеристики переходного процесса:
- время нарастания переходного процесса (Rise Time) – 9,6 сек;
- время регулирования (Setting Time) – 54 сек;
|
|
|
- установившееся значение выходной координаты (Final Value) –0,768;
- перерегулирование (Overshoot) составляет 18,6%.
Также с помощью с помощью LAT (Linear Analysis Tool) построим частотные и фазовые характеристики объекта управления.
Рисунок 2.20 - ЛЧХ автоматизированной системы регулирования расхода после модернизации
На графиках ЛАХ и ЛФХ (рис. 2.20) получены следующие значения:
- запас устойчивости по амплитуде (Gain Margin) – 6,57 дБ;
-запас устойчивости по фазе (Phase Margin)– 91,3 град.
Рисунок 2.21 - Амплитудно-фазовая характеристика системы регулирования после модернизации
Годограф АФЧХ не пересекает точку комплексной плоскости с координатами (-1;0) следовательно, модель устойчива с соответствующими запасами устойчивости по амплитуде и по фазе:
- запас устойчивости по амплитуде (Gain Margin) – 6,57 дБ;
-запас устойчивости по фазе (Phase Margin)– 91,3 град.
Для обеспечения заданных показателей качества и точности переходного процесса, а также выполнения требований по запасам устойчивости необходимо введение в систему линейного регулятора.
Для дальнейшего анализа необходимо определить величину статической ошибки.
Статическая ошибка системы εст показывает на сколько отличается уровень выходного сигнала от заданного его значения.
εст= узад - ууст (2.1)
где узад – заданное значение выходного сигнала;
ууст – установившееся значение.
Поскольку для получения переходных процессов используется единичный сигнал, то для управляющего воздействия узад = 1
εст =1 - 0.768 = 0.232
Очевидно, что статическую ошибку данной системы не получится устранить введением только регулятора, в связи с очень большим коэффициентом передачи датчика обратной связи. Необходимо, ввести последовательно с датчиком обратной связи звено, которое обеспечивало бы, коэффициент передачи по цепи обратной связи равный 1, т.е. установить нормирующий преобразователь с передаточной функцией:
|
|
|
 , (2.2)
, (2.2)
где 
Исходя из выше изложенных рекомендаций и учитывая применительно к нашей системе τ/Т=0,46, становится очевидно, что применение П- или И- регулятора с данным объектом не рекомендуется.
ПИ и ПИД регуляторы могут быть вполне применены. В данной выпускной квалификационной работе рассмотрим возможность использования ПИД - регулятора в АСР расхода реагента.
2.8.2 Оптимизация параметров настройки ПИД-регулятора
Для оптимизации параметров проектируемой системы регулирования, в программе MATLAB R2013b SIMULINK имеется библиотека Simulink Design Optimization, которая находится в Simulink Library Browser (рис. 2.21). Simulink Design Optimization используется для автоматической настройки параметров модели и при этом гарантирует соответствие модели всем требованиям к проектируемой системе, задаваемыми блоками Model Verification (рис. 2.22).

Рисунок 2.21 – Библиотека Simulink Design Optimization в Simulink Library Browser
Чтобы обеспечить требуемый переходной процесс по заданным графически ограничениям в окне временной области, необходимо воспользоваться блоком Check Step Response Characteristics (рис.2.22), который реализует метод динамической оптимизации. Задача оптимизации переменных с учетом наложенных ограничений, сформулированная в Check Step Response Characteristics - пакете, последовательно вызывает симуляцию работы модели системы регулирования в SIMULINK, сравнивает полученные результаты с заданными ограничениями переходного процесса и, используя градиентный метод, изменяет настраиваемые параметры для достижения заданной формы процесса.

Рисунок 2.22 – Библиотека блока Model Verification в Simulink Design Optimization
Рассмотрим работу блока Check Step Response Characteristic на конкретном примере. Будем использовать Check Step Response Characteristic для определения коэффициентов ПИД – регулятора. Начальной стадией является создание модели исследуемой системы после модернизации из стандартных блоков (рис. 2.23).

Рисунок 2.23 – Схема АСР для определения оптимальных параметров настройки ПИД – регулятора
Характеристики модели АСР до оптимизации коэффициентов ПИД –регулятора:
- время регулирования (Setting time) составляет: 54 сек.;
- установившееся значение выходной величины (Final value) составляет: 0,768;
- ошибка регулирования Ε ст = 1 - 0.768 = 0,232 (так как на входе единичное ступенчатое воздействие, то y зад = 1);
|
|
|
- перерегулирование (Overshoot) составляет: 0%;
Для начала настроим параметры блока PID Controller (рис. 2.24), вводя в поле параметра Proportional переменную Kp, в поле Integral - Ki, а в поле Derivative - Kd.

Рисунок 2.24 – Окно параметров ПИД – контроллера
Щелкаем два раза левой кнопкой мыши по блоку Check Step Response Characteristic, откроется окно блока оптимизации, в котором задаем необходимые параметры, подлежащие автоматической настройке (рис. 2.25).

Рисунок 2.25 – Окно Check Step Response Characteristics
Для нашей системы регулирования необходимы следующие параметры:
- время регулирования (Setting time) 40,1сек.;
- перерегулирование (Overshoot) 10%;
- установившееся значение выходной величины (Final value) 1;
- коридор ошибки регулирования (%Setting) 1%.
Значение время нарастания (Rise time) в нашей задаче не оговорено, поэтому берем его немного меньше величины Setting time.
Нажав кнопку Show Plot, мы получим коридор, в пределах которого должен находиться входной сигнал блока Check Step Response Characteristics в соответствии с требованиями задачи (рис. 2.26).

Рисунок 2.26 – Коридор параметров оптимизации
Перед началом оптимизации пакету Simulink Response Optimization, необходимо указать, какие величины следует изменять и настраивать. Нажимаем кнопку Response Optimization в окне Check Step Response Characteristics, переходим на вкладку Response Optimization, находим Desing Variables Set, выбираем New, и перетаскиваем оптимизируемые параметры из правого окна, в левое. Учитывая, что в качестве регулятора был выбран ПИД - регулятор, это будут символьные переменные Kp, Ki и Kd (рис. 2.27). После этого в командном окне MATLAB задаем начальные числовые значения для этих коэффициентов Kp=1; Ki=0; Kd=0.

Рисунок 2.27 – Ввод символьных имен коэффициентов, подлежащих автоматической настройке
После того, как задали значения Kp, Ki и Kd, нажимаем кнопку Optimize и наблюдаем за процессом оптимизации. Если процесс оптимизации завершился успешно, появится надпись зеленого цвета Optimization converged в окне Optimization Progress (рис. 2.28), и получим график результата процесса оптимизации (рис. 2.29).
|
|
|

Рисунок 2.28 – Окно Optimization Progress
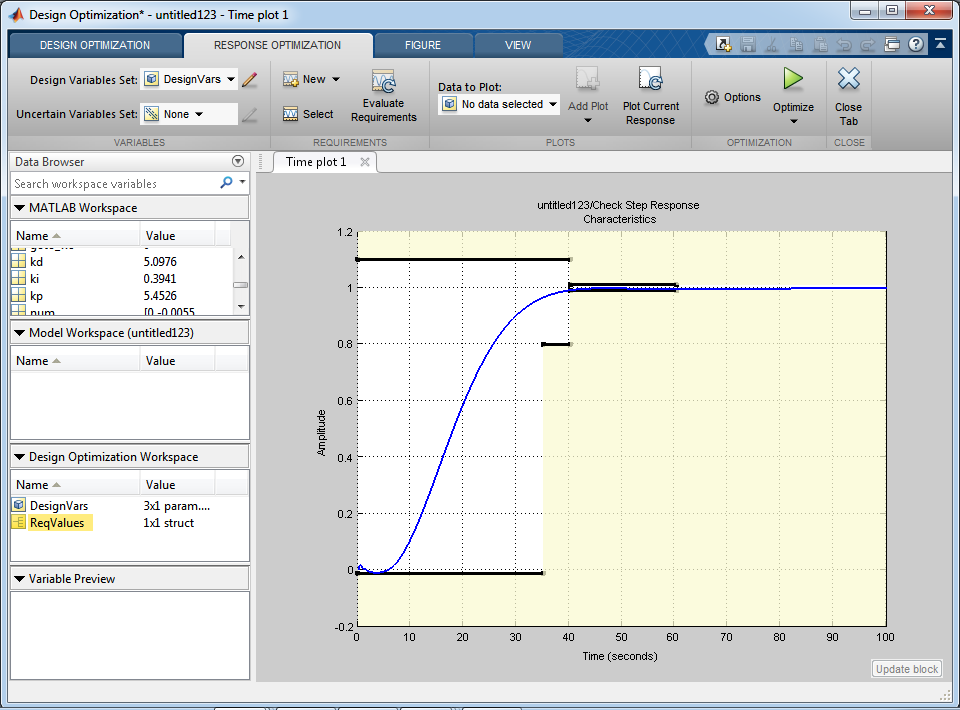
Рисунок 2.29 – График после оптимизации значений Kp, Ki и Kd
В итоге мы получили значения коэффициентов ПИД-регулятора Kp=5,4526, Ki=0,3941 и Kd=5,0976.
2.8.3 Анализ устойчивости и качества АСР после модернизации с ПИД - регулированием
Построим в SIMULINK функциональную схему АСР с ПИД - регулированием (рис. 2.30) и с помощью LAT (Linear Analysis Tool) получим переходную характеристику системы с оптимизированными данными на (рис. 2.31).

Рисунок 2.30 - Схема АСР после модернизации с ПИД - регулированием
Далее вводим оптимизированные данные в нашу систему и получаем переходную характеристику автоматизированной системы регулирования расхода после модернизации с оптимизированными настройками ПИД – регулятора (рис 2.31).
Рисунок 2.31 - Переходная характеристика АСР с оптимизированным ПИД - регулятором
На графике переходного процесса (рис. 2.31) представлен переходной процесс АСР с оптимизированным ПИД - регулятором. Основные характеристики переходного процесса следующие:
- время нарастания переходного процесса (Rise Time) – 19,9 сек;
- время регулирования (Setting Time) – 36,2 сек;
- установившееся значение выходной координаты (Final Value) – 0,998;
- перерегулирование (Overshoot) составляет 1,2%.
Определим статическую ошибку для модернизированной системы
εст = 1 – 0,998 = 0,002
Полученная характеристика удовлетворяет заданным требованиям к системе управления.
Для получения логарифмических, амплитудных и фазовых характеристик для определения запасов устойчивости по амплитуде и фазе необходимо разомкнуть систему (рис. 2.32).

Рисунок 2.32 - Схема разомкнутой АСР для снятия ЛЧХ, АФЧХ
Определим устойчивость системы и запасы устойчивости автоматизированной системы регулирования расхода после модернизации с оптимизированными настройками ПИД – регулятора (рис 2.33, 2.34).
.
Рисунок 2.33 - ЛЧХ автоматизированной системы регулирования с оптимизированным ПИД - регулятором
На графиках ЛАХ и ЛФХ (рис. 2.33) получены следующие значения запасов устойчивости:
- запас устойчивости по амплитуде (Gain Margin) – 10,5 дБ;
-запас устойчивости по фазе (Phase Margin)– 64,7 град.
Рисунок 2.34 - АФЧХ АСР с оптимизированным ПИД - регулятором
На графике (рис. 2.34) видно, что АФЧХ системы не охватывает точку с координатами (-1, j0), следовательно, замкнутая автоматизированная система регулирования расхода реагента является устойчивой.
Такой же вывод можно сделать из анализа ЛЧХ, так как ЛАХ пересекает ось абсцисс раньше, чем ЛФХ, окончательно спадая, переходит за значение –π (1800). Для данной системы ωс=0,052 рад/с, то есть ωс < ωπ и, следовательно, система устойчива.
|
|
|
Проведена идентификация установки БДР-25/2 как объекта автоматического регулирования расхода реагента ДНС. Проведена проверка на наблюдаемость и управляемость объекта управления. На основе анализа переходных характеристик системы управления был выбран наиболее подходящий для данного переходного процесса ПИД – регулятор. Проведена оптимизация настроечных параметров этого регулятора с помощью MATLAB 2013b.
В результате введения в систему ПИД- регулятора были получены параметры системы показанные в сводной таблице заданных и полученных значений (таблица 2.1).
Таблица 2.1 Параметры полученные до и после введения ПИД-регулятора
| Параметр | Значения до введения ПИД-регулятора | Значения после введения ПИД-регулятора |
| Статическая ошибка, % | 23,2 | 0,2 |
| Перерегулирование,% | 18,6 | 1,2 |
| Время регулирования, сек. | 36,2 | |
| Запас устойчивости по амплитуде, дБ | 6,57 | 10,5 |
| Запас устойчивости по фазе, град | 91,3 | 64,7 |
|
|
|


