 |
Моделирование не однородных систем.
|
|
|
|
Этапы системного анализа (5 этапов)
Анализ проблемы
Обнаружение проблемы
Точное формулирование проблемы.
Анализ развития проблемы (в прошлом и в будущем).
Определение внешних связей проблемы (с другими проблемами).
Выявление принципиальной разрешимости проблемы
Определение системы
- Специфика задачи.
- Определение позиции наблюдателя.
- Определение объекта.
- Выделение элементов (определение границ разбиения системы).
- Определение подсистем.
- Определение среды
Анализ структуры системы
- Определение уровней иерархии (в ВС).
- Определение аспектов и языков (в СС).
- Определение процессов функций (в ДС).
- Определение и спецификация процессов управления и каналов информации (в УС).
- Спецификация подсистем.
- Спецификация процессов, функций текущей деятельности (рутинных) и развития (целевых)
Формулирование общей цели и критерия системы
- Определение целей, требований надсистемы.
- Определение целей и ограничений среды.
- Формулирование общей цели.
- Определение критерия.
- Декомпозиция целей и критериев по подсистемам.
- Композиция общего критерия из критериев подсистем
Декомпозиция цели, выявление потребностей в ресурсах и процессах
1. Формулирование целей — верхнего ранга.
2. Формулирование целей — текущих процессов.
3. Формулирование целей — эффективности.
4. Формулирование целей — развития.
5. Формулирование внешних целей и ограничений.
6. Выявление потребностей в ресурсах и процессах
Типы Математических моделей
1. Модель идеального вытеснения – в соответствии с этой моделью принимается поршневое течение без перемешивания вдоль потока при равномерном распределении субстанции и направлении в перпендикулярном движении.
|
|
|
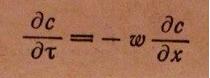
2. Модель идеального смешения – согласно этой модели, принимается равномерное распределение субстанции во всем потоке
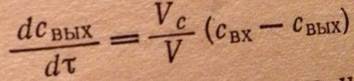
3. Диффузионная модель – различают однопараметрическую и двух параметрическую, диффузию модели
Однопараметрическая модель в данном случае, основной является модель вытеснения, осложненная обратным перемешиванием, следующему формальному закону диффузии

Двухпараметрическая модель в этой модели учитывается перемешивание потока в продольном и радиальном направлении, причем модель характеризуется коэффициентом продольного и радиального перемешивания.

4. Ячеечная модель – основной модели является представление об идеальном перемешивании в пределах ячеек, расположенных последовательно, и отсутствии перемешивания между ячейками.
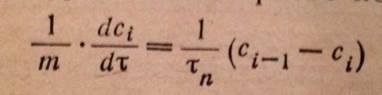
5. комбинированные модели, не все реальные процессы удается описать при помощи рассмотренных выше моделей. Типы комбинированных моделей
комбинированные модель смещения

комбинированные модель с байпасом

комбинированные модель циркуляцией и зонами вытеснения

комбинированные модель с циркуляцией по трем замкнутым контурам

Вопрос №3
Моделирование однородных систем.
Если изменение основных переменных процесса в пространстве не происходит, модели описывающие такие процессы называются однородными.
Вопрос №4
Моделирование не однородных систем.
Если изменение основных переменных процесса в пространстве так и во времени, или если указаны изменения происходят только в пространстве с размерностью большей 1, модели описывающие такие процессы называются не однородными.
6 Моделирование химической кинетики как пример динамической системы.
Построение модели требуется не только и не сколько знание математики, сколько глубокое понимание сущности описываемых явлений. Освоение методов кибернетики, химико-технологами создает базу для владения принципами построения математических моделей процессов химической технологии. Построение любой математической модели начинают с формализованного описания объекта моделирования. При этом наиболее общим примером разработки математического описания, является блочный принцип. Согласно этому принципу, составлению математического описания предшествует анализ отдельных процессов, протекающих в объектах моделирования. В начале исследуют гидродинамическую модель процесса как основу структуры математического описания. Изучают кинетику химических реакций, процессов массо- и теплопередачи с учетом гидродинамических условий найденной модели и составляют математическое описание каждого из этих процессов
|
|
|
Вопрос №7
Уравнение диффузии- представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным.
В смысле интерпретации при решении уравнения диффузии речь идет о нахождении зависимости концентрации вещества (или иных объектов) от пространственных координат и времени, причем задан коэффициент (в общем случае также зависящий от пространственных координат и времени), характеризующий проницаемость среды для диффузии
Уравнение обычно записывается так:
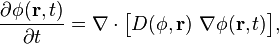
Уравнение теплопроводности — важное уравнение в частных производных, которое описывает распространение тепла в заданной области пространства во времени.
Для функции u(x,y,z,t) трёх пространственных переменных (x,y,z) и времени t, уравнение теплопроводности имеет вид:

где  — функция тепловых источников.
— функция тепловых источников.
|
|
|


