 |
Закон распределения дискретной случайной величины
|
|
|
|
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Пример 14. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения.
m
Вероятности пяти попаданий из пяти возможных, четырех из пяти и трех из пяти были найдены выше по формуле Бернулли и равны соответственно:
, 
, 
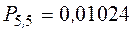Аналогично найдем:
.?
Представим графически зависимость числа попаданий от их вероятностей.
 |
При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.
Биноминальное распределение
Если производится 
независимых испытаний, в каждом из которых событие 
может появиться с одинаковой вероятностью 
в каждом из испытаний, то вероятность того, что событие не появится, равна 
.
Примем число появлений события в каждом из испытаний за некоторую случайную величину 
.
|
|
|
Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.
Значения найти достаточно просто. Очевидно, что в результате испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до раз.
Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.
Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.
Пример 15. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биноминальный закон распределения дискретной случайной величины – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.
m
Вероятность появления нестандартной детали в каждом случае равна 0,1.
Найдем вероятности того, что среди отобранных деталей:
1) Вообще нет нестандартных.
2) Одна нестандартная.
3) Две нестандартные детали.
4) Три нестандартные детали.
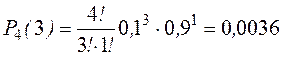
5) Четыре нестандартных детали.
 |
Построим многоугольник распределения.
Пример 16. Две игральные кости одновременно бросают 2 раза. Написать биноминальный закон распределения дискретной случайной величины – числа выпадений четного числа очков на двух игральных костях.
m
Каждая игральная кость имеет три варианта четных очков – 2, 4 и 6 из шести возможных, таким образом, вероятность выпадения четного числа очков на одной кости равна 0,5.
Вероятность одновременного выпадения четных очков на двух костях равна 0,25.
Вероятность того, что при двух испытаниях оба раза выпали четные очки на обеих костях, равна:
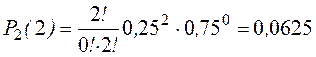
Вероятность того, что при двух испытаниях один раз выпали четные очки на обеих костях:
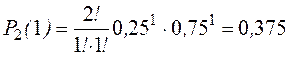
Вероятность того, что при двух испытаниях ни одного раза не выпаде четного числа очков на обеих костях:
|
|
|
.?
Распределение Пуассона
(Симеон Дени Пуассон (1781 – 1840) – французский математик)
Пусть производится независимых испытаний, в которых появление события имеет вероятность . Если число испытаний достаточно велико, а вероятность появления события в каждом испытании мало 
, то для нахождения вероятности появления события 
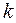раз находится следующим образом.
Сделаем важное допущение – произведение 
сохраняет постоянное значение:
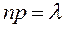
Практически это допущение означает, что среднее число появления события в различных сериях испытаний (при разном ) остается неизменным.
По формуле Бернулли получаем:
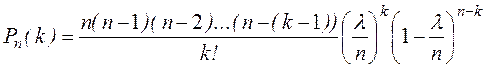
Найдем предел этой вероятности при 
.
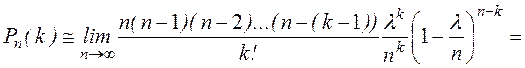
Получаем формулу распределения Пуассона:
Если известны числа 
и 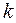, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.
|
|
|
