 |
Аналитические и численные решения
|
|
|
|
Точные аналитические решения дифференциальных уравнений движения замечательны тем, что описываемые такими решениями движения оказываются весьма простыми. В частности, классическая задача Кеплера о движении тела под действием центральной силы тяготения, обратно пропорциональной квадрату расстояния, имеет аналитическое решение, которое описывает сравнительно простые возможные движения по коническим сечениям. К сожалению, точные решения редко встречаются в физике. При наличии возмущающих воздействий (тяготение других планет, отличие силы тяготения небесного тела от строгой сферической симметрии, и т.п.) уравнения движения становятся неинтегрируемыми. Присущее кеплеровым движениям "чудо" замкнутых орбит, равно как и замечательная их простота, бесследно исчезают. Математическое исследование возмущенных движений неизмеримо усложняется.
Когда возмущающие воздействия малы по сравнению с основной силой тяготения, можно использовать приближенные аналитические методы. В некоторых случаях допустимо принять кеплерово движение в качестве нулевого приближения, считая, что возмущения вызывают сравнительно медленные изменения параметров кеплеровой орбиты, и попытаться найти аналитические выражения для этих медленных изменений. В задачах о межпланетных перелетах можно применять приближенный аналитический метод сопряженных конических сечений. Когда же возмущения нельзя считать малыми, как, например, в общем случае так называемой задачи трех тел, даже приближенные решения получить не удается. Тогда остается полагаться только на численные методы решения уравнений движения.
Поясним идею численных методов расчета движения. Пусть для некоторого начального момента времени заданы положение и скорость рассматриваемого космического тела (планеты, космического аппарата), а также расположение всех небесных тел, сообщающих ему ускорение своими силами тяготения. На основе закона всемирного тяготения можно вычислить гравитационное ускорение, сообщаемое данному телу каждым небесным телом в отдельности, а значит, и полное ускорение как векторную сумму этих ускорений. Зная величину и направление скорости тела, можно, учитывая вычисленное ускорение и считая его постоянным, рассчитать положение и скорость тела через небольшой промежуток времени ("шаг" интегрирования). Для найденного нового положения можно снова рассчитать ускорение тела, и затем по той же схеме рассчитать следующее положение тела и его скорость, и так далее. Таким путем можно шаг за шагом проследить все движение рассматриваемого тела.
|
|
|
Единственное приближение, которое при этом приходится допускать, заключается в том, что в течение каждого небольшого промежутка времени (шага расчета) ускорение тела считается постоянным, тогда как на самом деле оно все время изменяется. Но точность расчета можно повысить, уменьшая шаг интегрирования. Конечно, за повышение точности приходится платить увеличением объема вычислений.
Мы описали здесь так называемый алгоритм Эйлера численного интегрирования уравнений движения, известный также как метод ломаных. Этот метод дает сравнительно невысокую точность и приводит к накапливающимся ошибкам. Существует множество улучшенных модификаций алгоритма Эйлера. Например, можно предсказать для очередного шага новые положения тел (а значит и новые ускорения в конце этого шага), а затем повторить этот шаг еще раз, взяв для ускорения каждого из тел среднее между ускорением в начале данного шага и предсказанным ускорением для конца шага. При компьютерном моделировании обычно используют несколько более сложный метод Рунге − Кутта четвертого порядка точности, лишенный недостатков, присущих простому методу Эйлера. На практике проверить качество используемого численного алгоритма можно, применяя его к задаче Кеплера, и сравнивая результат с известным аналитическим решением.
|
|
|
При добавлении еще одного тела к системе двух взаимодействующих тел задача в общем случае становится аналитически неразрешимой, в то время как при использовании численных методов никаких принципиальных трудностей не возникает, лишь несколько возрастает объем необходимых вычислений.
Ограниченная задача трех тел
Для небесной механики и динамики космических полетов наиболее важна так называемая ограниченная задача трех тел. Она состоит в изучении движения тела P малой массы m3 под действием ньютоновского притяжения тел S и J, обладающих конечными массами m1 и m2 (m1 и m2 >> m3) в предположении, что тело малой массы не влияет на движение тел конечных масс.
Тем самым в ограниченной задаче тела S и J движутся по орбитам, определяемым задачей двух тел, так что их движение известно. Таким образом, анализ ограниченной задачи трех тел сводится к исследованию движения только одного тела P малой массы. Например, если пренебречь притяжением Солнца, то движение космического аппарата на трассе Земля-Луна с приемлемой точностью описывается в рамках ограниченной задачи трех тел.
Конечно, ограниченная задача значительно проще общей (неограниченной) задачи трех тел, но и ее общее решение не найдено.
В зависимости от формы орбит тел S и J конечных масс можно различать гиперболическую, параболическую и эллиптическую ограниченные задачи трех тел. Когда тела S и J движутся по окружностям, то говорят о круговой ограниченной задаче. Если тело P малой массы во все время движения находится в плоскости движения тел S и J, то говорят, что соответствующая ограниченная задача плоская. Если же тело P в своем движении выходит из плоскости орбит тел S и J, то говорят о пространственной ограниченной задаче.
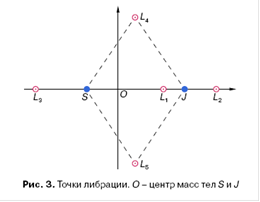
Со многих точек зрения удобно изучать движение тела P в системе координат, вращающейся вместе с телами S и J, выбрав единицу длины такой, чтобы и для некруговой задачи расстояние между телами S и J было постоянным. В этой системе координат упомянутым выше точным решениям задачи трех тел соответствуют фиксированные точки - положения равновесия тела P. Точки, лежащие на прямой, проходящей через S и J, обозначают через L1, L2 и L3, а точки, образующие равносторонние треугольники с телами S и J, обозначают через L4 и L5 (рис. 3). Если тело P поместить в Li с нулевой (во вращающейся системе координат) скоростью, то оно останется неподвижным. Точки Li часто называют точками либрации или либрационными центрами; L4 и L5 - треугольные, а L1, L2, L3 - прямолинейные (коллинеарные) точки либрации.
|
|
|
Вывод уравнений
Предваряя численное решение задачи, необходимо провести обезразмеривание переменных.
Уравнение движения тела в прямоугольной системе координат будет иметь вид:
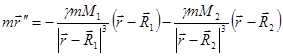(2)
Проведем обезразмеривание уравнения (2). Выберем в качестве единиц измерения расстояния и времени радиус орбиты R и период обращения T, соответствующие движению тела по окружности.
Введем безразмерные переменные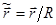 
, 
, 
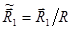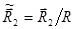и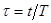 
. При этом скорость движения тела по окружности радиусом R будет равна
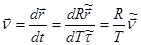,(3)
а величина ускорения
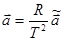.(4)
Отметим, что в этом случае при движении по круговой орбите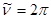 
, 
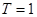и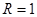 
. Подставим выражения (3) и (4) в (2):
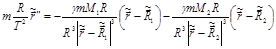,(5)
сократив общие множители в (5) получим
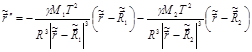.(6)
Период обращения может быть найден по формуле
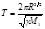.(7)
Подставив выражение (7) в (6) получим
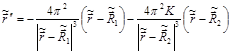,(8)
где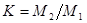 
.
Потенциал данной системы имеет вид:
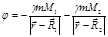.(9)
Произведем обезразмеривание (9) и вынесем общие множители
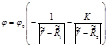,(10)
где 
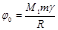, а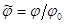 
.
Величина безразмерной кинетической энергии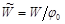 
будет равна
.(11)
Таким образом, полная энергия системы
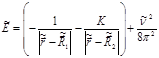.(12)
Технологическая часть
Программа производит расчет траектории движения тела под действием двух центров масс. Пользователь может менять входные данные, которыми являются:
(X1, Y1), (X2, Y2) - координаты соответственно первого и второго притягивающих центров;
|
|
|
Rx, Ry - начальные координаты тела;
Vx, Vy - скорость тела;
M1, M2 - массы соответственно первого и второго притягивающих центров;
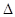W - кинетическая энергия тела.
На основании входных данных программа вычисляет скорость тела, потенциал и траекторию движения тела, строя при этом графики траектории и потенциала. Графики построены с использованием авто масштаба, но пользователь может самостоятельно выделить необходимый ему для наблюдения фрагмент графика.
В программе приведены расчеты и графики следующих типов движения тела:
. Инфинитное движение
Входные данные:
1 = 2
M2 = 1
Rx = -1.5= 0= 0= 9.734
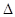W = 1.2
График траектории имеет вид:
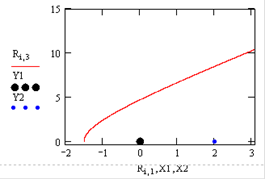
Тело движется по дуге параболы.
. Финитное движение вокруг двух притягивающих центров
Входные данные:
1 = 2
M2 = 1= -0.47= 0= 0= 11.922
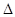W = 1.8
График траектории имеет вид:
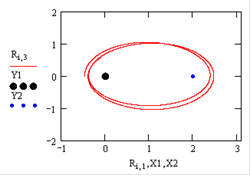
Тело совершает движение по эллипсу вокруг обоих центров масс.
. Финитное движение вокруг второго притягивающего центра
Входные данные:
1 = 2
M2 = 1= 1.7= 0 = 0
Vy = 6.283
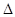W = 0.5
График траектории имеет вид:
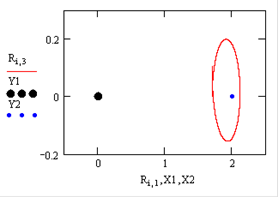
Тело движется по эллипсу вокруг второго притягивающего центра.
. Круговое движение вокруг первого притягивающего центра
в случае M1 >> M2
Входные данные:
1 = 2
M2 =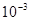 
= -1= 0= 0=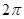 
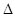W = 0.5
График траектории имеет вид:
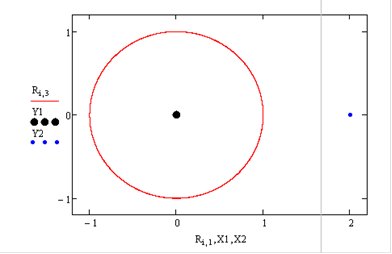
Тело совершает движение по окружности вокруг первого притягивающего центра.
Заключение
В рамках данной курсовой работы средствами системы MathCAD было осуществлено решение одной из важных задач небесной механики и динамики космических полетов - ограниченной задачи трех тел. Вычислены и показаны на графиках возможные траектории движения тела.
Литература
1. А.П. Маркеев. Задача трех тел и ее точные решения, 1999.
2. Е.И. Бутиков. Движения космических тел в компьютерных моделях.
. Кунин С. Вычислительная физика. - М. Мир, 1992.
. Поршнев С.В. Копьютерное моделирование физических процессов с использованием пакета MathCAD - М. Горячая линия - Телеком, 2002.
. www.exponenta.ru
|
|
|
