 |
Модель “Развивающейся” сети.
|
|
|
|
Модель представляет собой итерационный процесс, в котором на каждой итерации к web-графу добавляется по одной вершине. Пусть функция indegree(v) возвращает число входящих в вершину v дуг. Тогда новая вершина w соединяется с вершинами vk графа с вероятностью пропорциональной indegree(vk) (преференциальное добавление).
Для реализации модели, используется массив I[k] хранящий значения indegree(vk) + 1. Обозначим число уже добавленных к web-графу вершин g. Пусть I – сумма значений indegree всех вершин + количество вершин.
Все добавляемые вершины получают фиктивное значение indegree равное 1, что позволяет им быть выбранным в качестве конечной вершины дуги. Поэтому к I и было добавлено g.
Добавим к web-графу вершину w. Выберем случайное число r от 1 до I. Затем найдем вершину vk с наименьшим k, для которого выполняется следующее:
Вершина vk выбирается конечной вершиной новой дуги, а значение I[k] увеличивается на 1. Начальной вершиной дуги является добавленная вершина w.
При генерации массивных web-графов возникают две трудности:
· В оперативной памяти должен хранится массив I[j], что затруднительно при большом числе вершин.
· Процесс поиска подходящей конечной вершины vk существенно замедляется.
Для решения вышеописанных проблем используется следующее усовершенствование алгоритма:
В оперативной памяти хранится вспомогательный массив S из 
элементов. Каждый элемент массива S хранит сумму значений indegree для вершин. Т.о.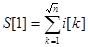 
, 
и т.д. Множество из вершин назовем блоком. Алгоритм генерации web-графа принимает следующий вид:
Фаза 1.
В оперативной памяти хранятся картежи tk, описывающие дуги, для которых известна начальная вершина, но не найдена конечная. Каждый картеж хранит номер блока, в котором находится конечная вершина дуги.
|
|
|
Пусть с – добавляемая вершина, она и будет являться начальной для новой дуги. Выберем случайное число r от 1 до I, где 
, а g = с – 1. Затем необходимо определить блок, в котором находится конечная вершина. Для этого найдем наименьшее k’, для которого выполняется следующее:
В память записывается картеж t <номер дуги; номер блока; относительная позиция внутри блока>, где за относительную позицию внутри блока принимается разность числа r и суммы значений indegree всех блоков, предшествующих найденному. Добавление вершин и генерация картежей продолжается до заполнения заданного объема памяти.
Фаза 2.
Создание дуг и запись их во внешнюю память. Для каждого блока ищутся все картежи, которые ссылаются на один блок. Затем этот блок загружается в оперативную память и в нем ищется конечные вершины описанных картежами дуг. Полученные дуги пишутся в буфер, выгружаемый во внешнюю память по мере заполнения, а значение indegree их конечных вершин увеличивается. Фаза завершает работу, когда для всех картежей будут сгенерированны дуги.
На практике часто используют многоуровневую систему блоков и специальные структуры, ускоряющие поиск вершины внутри них.
Копирующая модель сети.
На каждой итерации алгоритма к web-графу добавляется по одной вершине. Для каждой новой вершины v выбирается вершина-прототип p. Для всех исходящих из v дуг, с вероятностью 
конечная вершина выбирается среди всех вершин графа (“единообразный” выбор), а, с вероятностью 
, выбирается одна из конечных вершин исходящих дуг прототипа p (“копирование” дуги).
Отличительной особенностью этой модели является необходимость в большом числе операций чтения/записи из внешней памяти:
1. Алгоритм сохраняет сгенерированные дуги.
2. Считывает дуги, которые должны быть “скопированы”.
|
|
|
Для сокращения числа обращений к внешней памяти применяют модификацию модели, не требующей считывания копируемых дуг.
Пусть L – некоторое фиксированное число исходящих дуг. Сгенерируем для каждой вершины 1+2*L случайных чисел. Одно – для выбора вершины-прототипа, L – для конечных вершин, выбираемых “единообразно” и L значений , определяющих, копировать дугу прототипа или нет. Эти значения запоминаются за каждое фиксированное число итераций. Благодаря этому, если возникает необходимость “скопировать” дугу прототипа p, можно “вернуться” к моменту добавления p к графу и “пересчитать” исходящие из него дуги. Это может привести к цепи вычислений, но все они достаточно просты и проводятся в оперативной памяти, что заметно ускоряет работу алгоритма.
Результаты работы алгоритма записываются в буфер. При заполнении буфера, его содержимое переносится во внешнюю память, а сам буфер очищается.
Описанная выше модель является линейной. Существует ее т.н. “экспоненциальная” модификация, при которой на каждой итерации к web-графу добавляется не одна, а k вершин. Где k – функция, зависящая от размера графа.
Модель “Растущей сети”.
Модель была предложена в 2002г. D.M. Pennock и G.W. Flake. В своей работе они исследовали структуры web-графа, образованные тематическими наборами страниц. Их исследования показали, что распределение значений indegree в этих множествах сильно отличаются от экспоненциального. Распределение числа ссылающихся страниц в подобных группах более всего походит на “унимодальное с экспоненциальным хвостом”. Авторы выдвинули гипотезу, что экспоненциальный закон распределения является скорее исключением, чем правилом. Для реализации web-графа на уровне групп страниц с подобным распределением и была разработана модель “Растущей сети”.
Пусть мы имеем некий начальный граф, содержащий m0 вершин. На каждой итерации t к нему будет добавляться по одной вершине и m дуг. В модели развивающейся сети все m дуг соединяют новую вершину со старыми преференциально: Вероятность П(ki) того, что дуга соединит вершину i пропорциональна ki, где ki – текущее число дуг, инцидентных i.
В этой модели у всех вершин есть некая базовая вероятность быть соединенной с новой вершиной (единообразное добавление). Поэтому, вероятность соединения i-той вершины с новой, можно выразить следующей формулой:
|
|
|
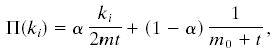
где m0 + t – число вершин, а 2mt – число дуг графа на t-й итерации.
При преференциальном добавлении, страницы на которые указывают множество ссылок имеют большее предпочтение при добавлении дуги. При единообразном – все страницы равноценны. Баланс между этими принципами дает более адекватную модель графа, т.к. web-дизайнеры при создании ссылок руководствуются 2 принципами:
· Ссылки ставятся на наиболее популярные страницы.
· Ссылки ставятся на наиболее интересные автору страницы, без учета их популярности.
При устремлении параметра a к 1 или m к 1 закон распределения числа входящих ссылок вновь станет близок к экспоненциальному.
Многослойная модель.
Как и все вышеописанные модели, многослойная модель является итерационной. В этой модели web-граф рассматривается как объединение нескольких регионов, называемых слоями. На каждой итерации t к графу добавляется вершина x, и ей присваиваются фиксированное число l регионов и d дуг, соединяющих x с вершинами графа.
рис. Многослойная модель графа.
Пусть Xi(t) – число вершин принадлежащих i-му слою на t-ой итерации.
L(x) – набор слоев, связанных с вершиной x.
Для связывания вершины x со слоями, в цикле l раз необходимо выполнить следующую операцию:
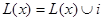, где i – слой, выбираемый из множества L/L(x) с вероятностью, пропорциональной Xi(t) с некоторым нормализующим фактором.
При генерации дуг при преференциальном добавлении рассматриваются только вершины одного слоя. Это позволяет генерировать слои “независимо” друг от друга. В связи с этим в многослойной модели выделяют 2 процесса: “поведение вне слоя” (extra-layer behavior) и “поведение внутри слоя” (intra-layer behavior).
Подобная независимость позволяет использовать для формирования слоев различные модели (Развивающейся сети, Копирующую модель, модель Роста сети и т.д.). При этом часть слоев может генерироваться одной моделью, а часть – другой.
|
|
|
В данной работе мы рассмотрим т.н. “гибридную” модель формирования слоев. Она была предложена авторами многослойной модели [16] и обладает большой устойчивостью при вариации параметров. “Гибридная” модель является сочетанием “Развивающейся” и “Линейной копирующей” моделей.
Между l слоями равномерно распределяются d дуг. Пусть с = [d/x] и 
- параметр копирования. В каждом слое i, с которым связана вершина x, она будет иметь с или с + 1 исходящую дугу, к которой необходимо подобрать конечную вершину. Обозначим за 
множество из Xi(t) вершин слоя i. Т.о. слой i будет состоять из вершин множества и дуг между ними, созданных за t-1 итерацию. Выберем из прототип p. Соединим x с помощью с дуг с вершинами множества следующим образом:
Для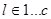 
с вероятностью l-я дуга соединяется с конечной вершиной l-й дуги прототипа p. Иначе, концом l-й дуги выбирается одна из еще на связанных с x вершин множества , с вероятностью, пропорциональной их нормализованному значению indegree + 1. Если прототип имеет лишь с исходящих дуг, а необходимо создать c+1, то она берется вторым способом.
Заключение.
Моделирование web-графа уже долгое время является самостоятельным и очень динамично развивающимся направлением исследований. Публикации, посвященные данной теме, появляются с завидной регулярностью. Также не может не радовать их доступность – подавляющее большинство из них можно найти в сети.
В последнее время активно обсуждается возможность модификации вышеописанных моделей: разрабатываются механизмы корректного изменения и удаления дуг и вершин, не ухудшающие свойства web-графа. Возможность подобных операций сделает модель более гибкой и позволит симулировать не только рост сети, но и ее распад. В свою очередь, это обеспечит изучение различных деструктивных процессов, таких как вирусная атака, отказ оборудования или просто резкое уменьшение числа пользователей некоторого сегмента web (например, в связи с прекращением работы какого-либо пирингового сервиса).
Также активно изучаются фрактальные свойства web-графа, его структурную эволюцию и влияние на нее большого числа появившихся за последние годы сервисов (напр. “живые журналы”, блоги, реферальные услуги и on-line игры). Возможно, глубокий анализ web-графа уже сейчас позволит нам “заглянуть в будущее” и узнать, на что будет похожа web через 3, 5, 10 лет, какие проблемы и перспективы нас ждут.
Растет и число программных продуктов, позволяющих генерировать качественные наборы данных. Особенно хочется отметить пакет WebGraph Framework II [17]. Он разработан группой ученых на платформе Java и содержит в себе не только механизмы генерации web-графов, но и различные инструменты и алгоритмы для работы с ними. Для хранения данных используется специально разработанное кодирование, позволяющее экономить внешнюю память, а также механизм, “на лету” определяющий необходимость извлечения данных из архива и их объем. [18]
|
|
|
Библиография.
1. S. Brin and L. Page. The anatomy of a large-scale hypertextual web search engines. In Proceedings of the 7th WWW Conference, 1998.
2. S. D. Kamvar, T. H. Haveliwala, C. D. Manning, G. H. Golub. Exploiting the Block Structure of theWeb for Computing PageRank. Stanford University.
3. P. Erdös, Renyi R. Publ. Math. Inst. Hung. Acad. Sci, 5, 1960.
4. R. Kumar, P. Raghavan, S. Rajagopalan, and A. Tomkins. Trawling the web for emerging cyber communities. In Proc. of the 8th WWW Conference, pages 403-416, 1999.
5. A.L. Barabasi and A. Albert. Emergence of scaling in random networks. Science, (286):509, 1999.
6. G. Caldarelli, P. De Los Rios, L. Laura, S. Leonardi, S.Millozzi. A study of stochastic models for the Web Graph. 2003
7. W Aiello, F Chung, and L Lu. A random graph model for massive graphs. In Proc. ACM Symp. on Theory of computing, pages 171{180, 2000.
8. R. Albert, H. Jeong, and A.L. Barabasi. Nature, (401):130, 1999.
9. Broder, R. Kumar, F. Maghoul, P. Raghavan, S. Rajagopalan, S. Stata, A. Tomkins, and J. Wiener. Graph structure in the web. In Proceedings of the 9th WWW conference, 2000.
10. D. Watts and S. Strogatz. Collective dynamics of small-world networks. Nature, (393):440, 1998.
11. J. Kleinberg. The small world phenomenon: an algorithmic perspective.
12. R. Kumar, P. Raghavan, S. Rajagopalan, D. Sivakumar, A. Tomkins, and E. Upfal. Stochastic models for the web graph. In Proc. of 41st FOCS, 2000.
13. G. Pandurangan, P. Raghavan, and E. Upfal. Using pagerank to characterize web structure.
14. D.M. Pennock, G.W. Flake, S. Lawrence, E.J. Glover, and C.L. Giles. Winners don't take all: Characterizing the competition for links on the web. Proc. of the National Academy of Sciences, 99(8):5207{5211, April 2002.
15. S. Dill, R. Kumar, K. McCurley, S. Rajagopalan, D. Sivakumar, and A. Tomkins. Self-similarity in the web. In Proceedings of the 27th VLDB Conference, 2001.
16. L. Laura, S. Leonardi, G. Caldarelli, and P. De Los Rios. A multi-layer model for the webgraph. In On-line proceedings of the 2nd International Workshop on Web Dynamics., 2002.
17. Paolo Boldi, Sebastiano Vigna. The Web Graph Framework I/II. Technical Reports 293-03/294-03, Università di Milano, Dipartimento di Scienze dell’Informazione, 2003. Available at http://webgraph.dsi.unimi.it/.
18. Paolo Boldi, Sebastiano Vigna. The Web Graph Framework II: Codes For The World–Wide Web
[1] Граф, при таком подходе, является неориентированным.
[2] Дуги web-графа должны быть неориентированными.
[3] Наряду с неявными, различают также явные кибер-сообщества: кольца (webrings), службы новостей и группы, образованные клиентами пиринговых сетей.
[4] Вершины степени 0 являются изолированными и обычно не рассматриваются, т.к. на практике они не встречаются.
|
|
|
