Проектирование цифрового фильтра: квантование параметров и анализ результатов

Теперь, после знакомства с основными причинами, порождающими эффекты квантования, вновь обратимся к нашей задаче проектирования цифрового фильтра. Ясно, что различие между АЧХ фильтра-прототипа и АЧХ квантованного фильтра (рис. 6) при выбранной структуре связано с установками параметров квантования. Как видно из рис. 7, в данном случае использовались форматы с фиксированной точкой [16, 15] и [32, 30], что соответствует значению fixed в поле Mode и значениям [16, 15] для квантователей Coefficient, Input, Output и Multiplicand в поле Format. Для квантователей Product и Sum используемый формат - [32, 30].

Для того, чтобы сравнить коэффициенты фильтров, нажмём кнопку " Коэффициенты фильтра" (рис. 2 б). В области отображения параметров распечатается следующая информация, показанная на рис. 12. Как видно из распечатки, все коэффициенты знаменателя передаточной функции фильтра-прототипа, за исключением последнего, превышают по модулю единицу, в то время как установленный формат для квантователя Coefficient равен [16, 15]. Это означает, что единственный бит, не предназначенный для хранения дробной части числа, является знаковым, то есть квантование любого числа, модуль которого больше или равен единице, приведёт к переполнению. Из-за эффекта переполнения коэффициенты знаменателя квантованного фильтра существенно отличаются от соответствующих коэффициентов фильтра-прототипа, что отмечено в начале каждой строки, за исключением последней, знаком " +" (переполнение в сторону плюс бесконечности) или " –" (переполнение в сторону минус бесконечности).

Попробуем промасштабировать коэффициенты так, чтобы они по модулю не превышали единицу. Это необходимо для повышения точности расчётов при реализации фильтров на DSP и осуществляется нажатием кнопки Scale transfer-fcn coeffs < = 1, расположенной в левой верхней части страницы Set Quantization Parameters. Для масштабирования используются коэффициенты, равные степени 2. После выполнения расчётов в поле Input/output scaling, расположенном под указанной кнопкой, появятся значения масштабных множителей, на которые умножаются входной и выходной сигналы фильтра с изменёнными коэффициентами. АЧХ фильтров будут выглядеть так, как показано на рис. 13.

Рисунок 13. Амплитудно-частотные характеристики фильтров после масштабирования коэффициентов

Помимо искажений АЧХ, в результате квантования появляются шумы, фильтр может стать неустойчивым, и возникнут разные виды генерации (например, генерация периодических колебаний, предельные циклы высокого и низкого уровней) [2], что в принципе затрудняет определение АЧХ. fdatool не позволяет решать задачи расчёта шумов арифметики, расчёта предельных циклов, оптимизации динамического диапазона и ряд других. Для некоторых из этих целей в MATLAB имеются специальные функции (например, nlm, limitcycle и другие). Однако, исключительно важное значение fdatool состоит в том, что он позволяет создавать нелинейные модели цифровых фильтров, весьма точно отражающих динамику реальных систем. Эти модели и являются объектами для упомянутых выше функций.

Возвращаясь к нашему примеру, щёлкнем мышью, поместив предварительно курсор в редактируемое окно Input/output scaling, нажмём на клавиатуре Enter, и затем нажмём клавишу Apply, находящуюся внизу главного окна fdatool. В области Current Filter Information появится сообщение " Stable: No". В том, что фильтр неустойчив, можно также убедиться, нажав на кнопку Pole/Zero Plot (на рис. 2 она обозначена как " Полюсы и нули" ). В результате появится карта нулей и полюсов, показанная на рис. 14, на которой видно, что передаточная функция построенного квантованного фильтра имеет полюсы, лежащие вне единичного круга.

Рисунок 14. Карта нулей и полюсов

Теперь попробуем решить поставленную задачу иначе, но прежде восстановим наши результаты, записанные на диск. Для этого выберем раздел Open Session меню File и откроем файл. В области Current Filter Information нажмём клавишу Convert Structure… и в открывшемся окне установим флажок Use second order sections (рис. 15), указав тем самым, что проектируемый квантованный фильтр должен быть реализован звеньями второго порядка. Нажатие кнопки Apply или OK инициализирует расчёт фильтра в указанной реализации. После вычислений можно убедиться, что АЧХ фильтра-прототипа и квантованного фильтра практически совпадают. Полученный результат показан на рис. 16. Важно обратить внимание на содержимое окна Input/output scaling: в нём распечатаны масштабирующие множители для сигналов на входе каждого из звеньев второго порядка, а также для выходного сигнала последнего звена.

Рисунок 15. Установка флажка Use second order sections в окне Convert Structure

Рисунок 16. Амплитудно-частотные характеристики фильтра-прототипа и квантованного фильтра, реализованного звеньями второго порядка

Итак, на первый взгляд задача, поставленная в разделе 3 (табл. 1), решена - цифровой фильтр с требуемыми характеристиками построен. Однако следует заметить, что частотная характеристика фильтра, и, в частности, АЧХ, показанная на рис. 16, построена по рассчитанным квантованным коэффициентам в предположении, что фильтр является идеальной линейной системой. Другими словами, при расчёте частотной характеристики учитывались лишь эффекты квантования коэффициентов фильтра. Для получения реальной частотной характеристики необходимо учесть нелинейные эффекты квантования, связанные с формой реализации (структурой) фильтра и квантованием других параметров, устанавливаемых на странице Set Quantization Parameters.

Чтобы получить частотную характеристику фильтра, построенную с учётом указанных факторов, следует выполнить комплексную проверку его работы на основе имитационного моделирования. Рассмотрим, как можно определить АЧХ, вообще говоря, нелинейной системы, используя одну из функций MATLAB - nlm (noise loading method), которая вычисляет оценку частотной характеристики квантованного фильтра с учётом всех эффектов квантования. Функция, на основе метода Монте-Карло, выполняет L испытаний, в каждом из которых моделируется прохождение входного сигнала, представляющего собой белый шум, через исследуемый фильтр. По результатам каждого испытания находится оценка частотной характеристики фильтра по спектрам входного и выходного сигналов. Итоговая оценка частотной характеристики вычисляется усреднением оценок частотных характеристик по всем испытаниям.

Перед тем, как воспользоваться функцией nlm, экспортируем наш фильтр в рабочее пространство MATLAB (Work-space). Это выполняется следующим образом. В меню File выбрать раздел Export, в появившемся окне указать, куда экспортировать (Workspace) и имя фильтра (например, Hq1), после чего нажать кнопку OK. После выполнения команды надо перейти в командное окно MATLAB и набрать команду

> > nlm(Hq1, [], 50),

по которой будет выполнено моделирование, включающее 50 испытаний. В результате появится окно с графиками АЧХ и ФЧХ, показанное на рис. 17, из которых видно, что построенная нами нелинейная цифровая система, каковым является квантованный фильтр, не удовлетворяет заданным требованиям, изложенным в табл. 1 и показанным на рис. 4. Отметим, что функцию nlm можно вызвать, указав лишь имя фильтра:

> > nlm(Hq1).

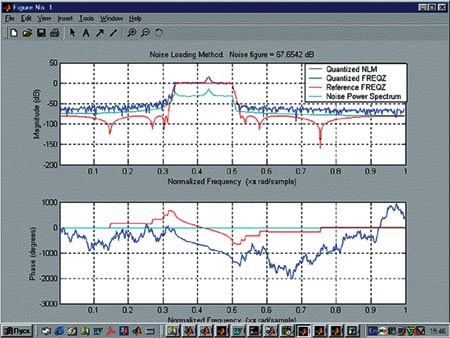
Рисунок 17. Результаты моделирования с помощью функции nlm

В этом случае число испытаний L будет выбрано по умолчанию (L = 10), и получаемые графики будут менее сглаженными.

Очевидно, что для получения желаемого результата нам надо изменить параметры квантования, задаваемые на странице Set Quantization Parameters. Попробуем для всех квантователей, кроме квантователей коэффициентов, переустановить способ округления с floor в convergent и рассчитать новый квантованный фильтр, нажав кнопку Apply. Если затем импортировать полученный фильтр в Workspace и повторить вызов функции nlm к этому фильтру, получим частотную характеристику, показанную на рис. 18. Сравнивая графики, показанные на рис. 17 и 18, видно, что АЧХ последнего фильтра является лучшим приближением к требуемому результату, однако она тоже не удовлетворяет заданным требованиям.

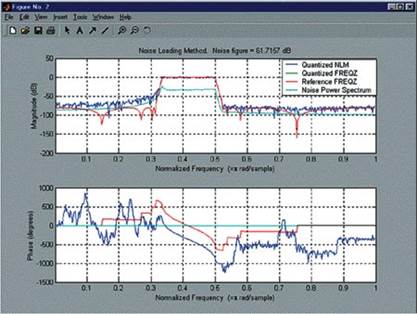
Рисунок 18. Результаты моделирования с помощью функции nlm после замены способа округления с floor на convergent

Обратимся снова к странице Set Quantization Parameters и установим форматы квантователей в соответствии с рис. 19. Повторив процедуру расчёта, импорта и испытания фильтра с помощью nlm, получим результат, показанный на рис. 20. Как видно из рисунка, АЧХ фильтра-прототипа и квантованного фильтра практически совпадают, то есть полученный фильтр удовлетворяет требованиям, изложенным в табл. 1.

Рисунок 20. Результаты моделирования с помощью функции nlm после замены форматов квантователей

Заключение

Материал, изложенный в настоящей статье, следует рассматривать как введение в GUI-fdatool, позволяющее решать ряд практически важных и теоретически интересных задач, связанных с проектированием цифровых фильтров. Главное - это возможность весьма точно моделировать разнообразные структуры цифровых фильтров в режиме нелинейных преобразований, связанных с эффектами квантования, и возможность оценивать интегральные параметры фильтров.

Вместе с тем, многие вопросы синтеза цифровых фильтров с оптимальными либо близкими к таковым характеристиками и учитывающие нелинейные эффекты квантования остались за пределами этой публикации, равно как и за пределами системы MATLAB. Наиболее полную информацию о работе с программой читатель может найти в справочной системе MATLAB [3]. Для этого надо в окне справки MATLAB (окно help) открыть раздел Filter Design Toolbox Using Filter Design Toolbox Quantization Tool Overview.