 |
NonLinear Iterative Partial Least Squares (NIPALS) Algorithm
|
|
|
|
МГК
Общий вид модели МГК:
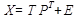, где 
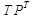- объяснённые данные, Е - шумы.
Перед расчётом исходные данные необходимо автошкалировать!
Нахождение ГК основывается на собственных векторах (eigenvector).
Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.
Алгоритм NIPALS - один из распространённых методов отыскания собственных векторов, МГК обычно основывается на этом алгоритме.
http: //mathprofi. ru/sobstvennye_znachenija_i_sobstvennye_vektory. html - понятное описание собственных значений и векторов.
NonLinear Iterative Partial Least Squares (NIPALS) Algorithm
Алгоритм за один цикл находит одну главную компоненту.
Существуют разные реализации этого алгоритма, я взял отсюда:
https: //www. mathworks. com/matlabcentral/fileexchange/42142-nipals-algorithm-for-principle-component-analysis/content/nipals. m? requestedDomain=www. mathworks. com - встроенная в Matlab функция, которая выполняет ту же задачу, но имеет другое количество аргументов (и вообще, брать готовые непонятные функции - не наш метод).
Порядок работы алгоритма:
1. Начальные условия, выбор первого столбца в качестве первой компоненты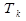 
, где k = 1: N - текущая ГК, где N - число вычисляемых ГК.
Tk = X(:, 1);
2. Нахождение приближённых значений вектора нагрузок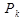 
для текущих начальных условий путём проекции исходной матрицы на вектор ГК
Pk = (X'*Tk/(Tk'*Tk));
3. Нормирование полученного значения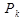
Pk = Pk/norm(Pk);
4. Уточнение вектора счетов
Tk2 = X*Pk/(Pk'*Pk);
5. Вычиление конвергенции(сходимости) (ежели текущий вектор 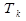близок к собственному вектору, то разность 
стремится к нулю)
|
|
|
d0 = (Tk2-Tk)'*(Tk2-Tk);
6. Присваивание уточнённого значения вектора счетов текущему для следующей итерации
Tk = Tk2;
7. Проверка конвергенции: ежели меньше константы, например 0. 0001, значит k-тая ГК найдена, поиск следующей компоненты. ежели нет, переход на п. 2
8. Вычитание вклада найденной ГК из исходных данных,
X = X - Tk*Pk';
добавление найденной ГК в конечную матрицу счетов и нагрузок
T(:, k) = Tk;
P(:, k) = Pk;
Полностью код алгоритма может выглядеть таким образом:
for k = 1: nc
% перебор по всем ГК
Tk = X(:, 1); % шаг 1
d0 = 1; % переменная для конвергенции
while d0 > 0. 0001
% шаг 7, цикл по проверке конвергенции
Pk = (X'*Tk/(Tk'*Tk)); % шаг 2
Pk = Pk/norm(Pk); % шаг 3
Tk2 = X*Pk/(Pk'*Pk); % шаг 4
d0 = (Tk2-Tk)'*(Tk2-Tk); % шаг 5
Tk = Tk2; % шаг 6
end
X = X - Tk*Pk'; % шаг 8
T(:, k) = Tk; % шаг 8
P(:, k) = Pk; % шаг 8
end
Определение объяснённой и необъяснённой дисперсий
Объяснённой дисперсией называют процент общей дисперсии, который покрывается найденными главными компонентами, называют TRV. Необъяснённая - дисперсия остатков, называют ERV. Исходная матрица данных является 100% необъяснённой.
Один из вариантов вычисления дисперсий - по матрице остатков E. Матрица остатков - это исходная матрица Х за вычетом данных, объясняемых найденными на этом этапе главных компонент (шаг 8).
При нахождении объяснённой дисперсии сначала вычисляют дисперсию каждого примера:
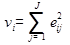, где j - число признаков. Здесь дисперсия имеет более короткий вид потому что данные центрированы и среднее равно нулю.
Вычисляют коэффициент v0, общий для всех признаков:
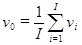
Объ. дисперсия k-той главной компоненты равна:
Необъяснённая дисперсия равна:
где TRV(0) - численное значение объяснённой дисперсии исходных данных, принимаемое за условные 100%.
Вычисление vi:
[r c] = size(X);
|
|
|
v = zeros(r, 1);
for i = 1: r
for j = 1: c
v(i) = v(i) + X(i, j)^2;
end
end
Вычисление v0:
v0 = sum(v). /r;
Вычисление объяснённой дисперсии
TRV(k) = v0/c;
Необъяснённая дисперсия
ERV(k) = 1 - TRV(k)/TRV0
Здесь TRV0 вычислена таким же образом, для исходных данных.
|
|
|
