 |
Описание. Алгоритм. Применение
|
|
|
|
ЛДА
Описание
Суть метода в нахождении дискримнантных функций (ДФ) вида:
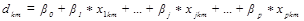
Затем анализируемые данные подставляют в ДФ и получают результат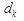 
, называемый проекцией точки на ДФ, при этом классы в новом k-мерном пространстве имеют максимально возможное разделение. Размерность k равна числу ДФ и в общем случае равна числу классов минус один (G-1).
Данный метод является методом с учителем, что означает необходимость заранее предоставить репрезентативную выборку для всех анализируемых классов. В данном случае программа составляется для случая, когда в каждом классе одинаковое число точек. В противном случае необходима корректировка расчёта средних значений.
Алгоритм
В программе будут использоваться следующие переменные, которые, например, могут иметь следующие значения:
G = 2; % число классов
P = 38; % число признаков (сенсоров)
N = 50; % число примеров классе, для упрощения одинаково для всех классов
% Xj - массив размером N на P с точками j-го класса, j=1: 5
1. Исходные данные необходимо автошкалировать.
см. выше, уже было
2. Находятся средние значения
- внутригрупповые для каждого класса (по каждому признаку)
for i=1: P
Xsr(1, i) = mean(X1(:, i)); % среднее 1 класса
Xsr(2, i) = mean(X2(:, i)); % среднее 2 класса
end
- межгрупповое среднее (для определения первого центроида)
Xsr_mgr = mean(Xsr); % межгрупповое среднее всех классов
3. Находятся матрицы отклонений
- межгруппового отклонения, матрица H
H = zeros(P); % объявление заранее, здесь нужно
for j = 1: 1
H = H(:,: ) + (Xsr(j,: ) - Xsr_mgr(1,: ))'*(Xsr(j,: ) - Xsr_mgr(1,: ));
end
- внутригрупповых отклонений - ковариации между всеми признаками по каждому классу
C1 = zeros(P); % объявление заранее
|
|
|
for i=1: P % первый цикл по числу признаков
for j=1: P % второй цикл по числу признаков
for k=1: N % цикл по числу примеров в классе
sum_bufer = (X1(k, i)-Xsr(1, i))*(X1(k, j)-Xsr(1, j));
C1(i, j) = C1(i, j) + sum_bufer;
end
end
end
C1 = С1 / N;
Такие же вычисления проделать для всех классов.
4. Находится матрица M из матриц ковариаций, по формуле:
M = zeros(G); % Объявление заранее
M = M + N*C1;
M = M + N*C2;
M = M + N*C3;
5. Находятся собственные вектора исходя из формулы:
где M - вышеприведённая какая-то матрица, H - межгрупповое отклонение, 
- собственное значения, w - собственный вектор.
M1 = M\H;
% \ - деление матрицы справа налево; почему-то
% по-другому не поделилось
[w lambda] = eigs(M1); % вычисление главных значений
Здесь применена стандартная функция eigs(), которая возвращает матрицу собств. векторов (w) и диагональную матрицу собств. значений (lambda). Каюсь, ручное вычисление собственных векторов я ниасилил =(
Собств. вектора w, соответствующие собств. значениям 
, и порождают дискриминантные функции. Но перед использованием коэффициенты векторов нужно стандартизировать (в некоторых книгах не стандартизируют, но тогда эти результаты не будут сходиться с результатами других программ)
6. Стандартизация дискриминантных коэффициентов:
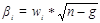
где n - общее число примеров по всем классам, g - число классов;
b0 = zeros(P, 1);
for i=1: K % Перебор по числу ДФ
for j=1: P % Перебор по числу классов
b(i, j) = w(i, j)*(K^0. 5);
b0(i) = b0(i) + b(i, j)*Xsr_mgr(j);
end
end
В итоге получится матрица b, и b0, где каждая строка - коэффициенты соответствующей ДФ.
Тогда, например, для j-го примера класса k размерностью в p признаков результат первой ДФ будет равен:
Применение
Пусть имеется 3 класса по 3 признака, и по 2 примера в каждом классе. График по первым двум признакам:
Здесь видно, что класс 1 (красный) пересекается с классом 2 (синий) по оси Y, и класс 2 пересекается с классом 3 по оси Х.
|
|
|
После вычисления ДФ имеет матрицу b0 2x1 и b размерностью 2х3. Здесь первая строка обоих матриц - одна ДФ, 1 столбец матрицы b -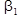 
, второй - 
и т. д.
Для получения данных в новом пространстве ДФ необходимо умножить исходные матрицы таким образом, чтобы в каждом примере значение данных каждого признака было умножено на соответствующий признаку коэффициент ДФ; производится суммирование всех произведений для каждого примера, затем суммируется с соответствующим ДФ коэффициентом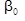 
.
Например, пусть df1 - результирующая матрица для первого класса, где первый столбец соответствует первой ДФ, второй столбец - второй ДФ, а каждая строка - примеры данных. Тогда вычисление результирующих матриц для каждого класса будет иметь вид:
df1(:, 1) = b0(1) + X1s(:, 1). *b(1, 1) + X1s(:, 2). *b(1, 2) + X1s(:, 3). *b(1, 3);
df2(:, 1) = b0(1) + X2s(:, 1). *b(1, 1) + X2s(:, 2). *b(1, 2) + X2s(:, 3). *b(1, 3);
df3(:, 1) = b0(1) + X3s(:, 1). *b(1, 1) + X3s(:, 2). *b(1, 2) + X3s(:, 3). *b(1, 3);
df1(:, 2) = b0(2) + X1s(:, 1). *b(2, 1) + X1s(:, 2). *b(2, 2) + X1s(:, 3). *b(2, 3);
df2(:, 2) = b0(2) + X2s(:, 1). *b(2, 1) + X2s(:, 2). *b(2, 2) + X2s(:, 3). *b(2, 3);
df3(:, 2) = b0(2) + X3s(:, 1). *b(2, 1) + X3s(:, 2). *b(2, 2) + X3s(:, 3). *b(2, 3);
График имеет следующий вид (здесь df1 - красным, df2 - зелёным, df3 - синим)
Таким образом, видим более отчётливое разделение на классы. Помимо этого сокращается размерность (в этом случае с трёх до двух).
|
|
|
