 |
Определение площади графическим способом
|
|
|
|
Сущность графического способа состоит в том, что площадь участка на плане разбивается на простейшие геометрические фигуры - прямоугольники трапеции, треугольники. По формулам геометрии определяют площади отдельных фигур и подсчитывают общую площадь участка. Наилучшим вариантом разбивки является деление участка на равносторонние треугольники. Точность определения площади участка зависит от числа взятых фигур и углов границы участка. Точность измерения повышается в результате повторных измерений и при новой разбивке участка на другие фигуры. За окончательный результат принимают среднее арифметическое из всех измерений.
Как правило, конфигурации участков леса, пашен, лугов, болот и т.д. имеют неправильные геометрические формы. Поэтому для измерения площадей небольших участков с криволинейным контуром применяют квадратные или параллельные палетки на прозрачном материале (рис. 2 а, б).

Рис. 2. Палетки: а - квадратная; б – параллельная
Квадратная палетка представляет собой квадрат со стороной 1 дм, который разбит на сеть средних квадратов со стороной 1 см, средние квадраты разбиты на сеть малых квадратов со стороной 2-5 мм.
Площадь участка определяется подсчетом больших, средних и малых квадратов, заключенных в фигуре участка. Для повышения точности и контроля измерение площади участка следует производить повторно, меняя положение палетки относительно контура участка.
Недостатком применения квадратных палеток является то, что доли палеток оцениваются на глаз и подсчет числа клеток затруднителен. Этого недостатка можно избежать при применении параллельных палеток (рис. 2, б).
Здесь параллельные линии проведены на расстоянии 5 мм одна от другой. Палетку накладывают на криволинейный контур участка так, чтобы какие-нибудь две линии палетки касались контура (А и В). В этом случае можно считать, что площадь участка разбивается палеткой на ряд трапеций с основаниями ai,a2,..., ап и постоянной высотой h.
|
|
|
Крайние части палетки с точками А и В следует считать трапециями с основаниями, равными нулю. Общая площадь участка S будет равна:
S = h (a1+ a2+...+ an)

Рис.3.

Рис.4
Расчетно-графическая работа № 2
Тема: Оценка точности ряда неравноточных измерений одной величины

Рис 1.
L – нивелирные хода, Рп – исходные пункты, А – узловая точка
Дано: нивелирная сеть из 6-ти ходов различной длины пройденных от твердых реперов и сходящихся в угловой точке А.
Требуется:
1. Найти вес каждого хода, приняв один из них за эталонный (за единицу веса)
2. Найти среднее весовое значение высотной отметки узловой точки 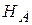 .
.
3. Найти с.к.о. (среднюю квадратическую ошибку) единицы веса  .
.
4. Найти с.к.о. среднего весового значения отметки узловой точки  .
.
5. Найти с.к.о. измеренных превышений для каждого нивелирного хода 
Таблица измерений
| № ходов | Значение
Отметки  , м , м
| L, км |  см
см
| Вес хода

|  ,
см ,
см
|  м
м
|  см см
| 
|  ,
см ,
см
|
| 536,39 | 11,0 | ||||||||
| 536,37 | 10,0 | ||||||||
| 536,36 | 8,3 | ||||||||
| 536,48 | 18,2 | ||||||||
| 536,50 | 21,3 | ||||||||
| 536,42 | 16,1 | ||||||||

|
- Найдем вес хода:
 пример:
пример:  С=10 км. Аналогично и для остальных ходов.
С=10 км. Аналогично и для остальных ходов.
- Находим среднее взвешенное:


где  -уклонение
-уклонение
H0 -минимальное значение отметки точки А; примем что H0= 536,36 м
- Найдем с.к.о. единицы веса:


- Найти с.к.о. среднего весового значения отметки узловой точки т.А

|
|
|
- Найти с.к.о. измеренных превышений для каждого нивелирного хода.

аналогично и для остальных ходов, результаты сводятся в таблицу измерений.
Список литературы
- Большаков В.Д. Справочник геодезиста (в двух книгах) ]/Большаков В.Д Левчук Г.П. - М.; Недра, 1975. - 1056 с.
- Маслов А.В. Геодезия / Маслов А.В., Гордеев А.В., Батраков Ю.Г.-М.: КолосС, 2006. – 598с.
- Дубинок Н.К. Землеустройство с основами геодезии. –М.: Колосс., 2003.
- Неумывакин Ю.К. Геодезическое обеспечение землеустроительных работ. М.: Недра, 1996.
|
|
|


