 |
Сжатие по методу Д. Хаффмана
|
|
|
|
УО «БГУИР»
кафедраинформационных технологий автоматизированных систем
РЕФЕРАТ
на тему:
«Научные проблемы Интернета»
МИНСК, 2008
Научные проблемы Интернета группируются вокруг следующих задач:
· Защита информации
· Сжатие информации
· Поиск информации
· Распознавание информационных объектов (текста и образов)
· Прогнозирование временных рядов
· Классификация документов
· Выбор и оценка многокритериальных альтернатив
· Принятие решений и логический вывод и др.
Рассмотрение всех этих задач выходит за рамки настоящего труда. Рассмотрим только некоторые задачи.
Защита информации
Современные способы защиты информации используют в первую очередь различные методы шифрования. Мы рассмотрим здесь два криптографических метода: RSA и DES. Основные принципы криптографии можно сформулировать следующим образом.
1. В шифровании основную роль играет не алгоритм, а ключ.
2. Алгоритм шифрования должен быть таким, чтобы шифрование выполнялось легко и эффективно с вычислительной точки зрения; наоборот, дешифрование должно представлять собой сложнейшую математическую задачу (например, переборного типа).
Алгоритм RSA. Пусть необходимо передать по линии связи числа x (рассмотрим здесь только целые положительные числа). Вместо числа x передают число y, вычисляемое по формуле
 , ,
| (1.1) |
где e и m являются открытыми числами (известны всем абонентам сети).
Требуем, чтобы e и m были взаимно простыми числами (т.е. не числами общих делителей, кроме 1, причем  ).
).
Оказывается, что зная y, e и m, найти x – сложнейшая математическая задача. Пока же продемонстрируем, как найти y по x, e, m.
Операция
|
|
|

| (1.2) |
находит целочисленный остаток a от деления b на m. Например,
2 = 17 mod 5
или
1 = 41 mod 8.
Но пусть требуется найти
630 mod 18 =?
Это сделать посложнее. Мно записать
630 = 2*315 = 2*5*63 = 2*5*7*9 = 63*10.
Теперь можно использовать правило разложения на множители
 .
.
В самом деле, пусть
 ,
,
 ,
,
 .
.
Тогда
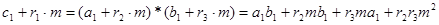 .
.
Последняя сумма дает остаток от деления на m, равный  . Но
. Но  ,
, 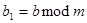 . Поэтому
. Поэтому
 .
.
Теперь нетрудно это правило применить, скажем, к
713 mod 8 =?
Запишем
 .
.
Имеем  . Поэтому
. Поэтому  .
.
Обратимся теперь к формуле (6.16).
Пусть  ,
,  ,
,  .
.
Найдем
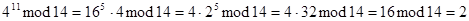 .
.
Итак,  . Это значение и будет передано по сети вместо x.
. Это значение и будет передано по сети вместо x.
Теперь рассмотрим, как восстановить x по y, m, e. Для этой цели нужно найти число d, удовлетворяющее условию
 , ,
| (1.3) |
где  – значение функции Эйлера от числа m. Функция Эйлера вычисляется сравнительно просто. Так,
– значение функции Эйлера от числа m. Функция Эйлера вычисляется сравнительно просто. Так,
 . .
| (1.4) |
Если p простое число и r – целое, то
 . .
| (1.5) |
Формул (1.4) и (1.5) достаточно для того, чтобы найти функцию Эйлера для любого целого положительного числа. В нашем случае получаем:
 .
.
Для любознательных читателей отметим, что значение  равно числу целых чисел на отрезке 1.. m, взаимно простых с m. Отыскание значения функции Эйлера для больших целых чисел является вычислительной задачей очень большой сложности.
равно числу целых чисел на отрезке 1.. m, взаимно простых с m. Отыскание значения функции Эйлера для больших целых чисел является вычислительной задачей очень большой сложности.
Пример.  . Все четыре числа: 1, 2, 3, 4 взаимно просты с m.
. Все четыре числа: 1, 2, 3, 4 взаимно просты с m.
Теперь обратимся к уравнению (3.3). В этом уравнении d играет роль секретного ключа. Решить уравнение (3.3) путем перебора значений d можно, но если в числе m, например, 100 цифр, то на вычисление d уйдет достаточно много времени. Для небольших значений, таких как в нашем примере, можно воспользоваться алгоритмом решения уравнений в целых числах, который мы и приведем.
Итак, в нашем примере уравнение такое:
 . .
| (1.6) |
Уравнение (1.6) можно переписать следующим известным образом:
|
|
|
 . .
| (1.7) |
В (1.7) r и d неизвестные целые числа. Представим (1.7) в виде системы двух линейных неравенств.
 ,
,
 ,
,
или, что эквивалентно:
 , ,
 . .
| (1.8) |
В неравенстве с положительной правой частью выделим член с минимальным по модулю коэффициентом и разрешим неравенство относительно этого члена:
 ,
,  .
.
Отсюда легко получить отсекающее неравенство:
(a)  ,
(b) ,
(b) 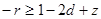 ,
(c) ,
(c)  . .
| (1.9) |
Здесь z – новая целочисленная переменная. Заметим, что переход от (a) к (b) в (1.9) правомерен, так как r, d, z – целочисленны.
Выполним подстановку (3.9) в систему (1.8). Получим новую систему:
 , ,
 . .
| (1.10) |
Обратим внимание на следующее принципиальное обстоятельство. В сравнении с (1.8) значение минимального коэффициента понизилось. Этот факт можно строго обосновать. Следовательно, весь процесс должен закончиться рано или поздно одним из двух результатов:
1) минимальный коэффициент по модулю станет равным 1 (как в (1.10)); будет получена система вида
 ,
,
 ,
,
где a и b – взаимно просты (в этом случае нет решения в целых числах).
В первом случае процесс решения завершен. Получаем из (1.10) подстановку для d:
 . .
| (1.11) |
Тогда из (1.9) найдем:
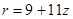 . .
| (1.12) |
Итак, формулы (1.11) и (1.12) и дают нам итоговые подстановки для d и r из (1.7). Например, пусть 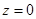 . Тогда
. Тогда  ,
,  . Возьмем именно это значение для минимального d.
. Возьмем именно это значение для минимального d.
Итак, мы подошли к решающему моменту: наш секретный ключ  . Получили число
. Получили число 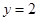 ,
,  ,
,  .Восстанавливаем x по формуле:
.Восстанавливаем x по формуле:
 . .
| (1.13) |
Итак,  .
.
Все сошлось. Возьмем, например,  . Тогда
. Тогда  ,
,  :
:
 (ответ тот же).
(ответ тот же).
Таким образом, не имеет значения, какое z брать для получения d.
Метод RSA мы завершим следующим замечанием.
Метод RSA вообще говоря требует, чтобы m было большим простым числом. Для установления факта, что m – простое, можно использовать малую теорему Ферма:
 . .
| (1.14) |
В (1.14) a и p должны быть взаимно просты, а p – простое число.
Пример.
 ,
,  :
:
 .
.
 ,
,  :
: 
 .
.
К сожалению, формула (1.14) справедлива также для некоторых составных чисел. Поэтому чтобы применить ее на практике, нудно выполнить проверку для некоторых различных a (идея алгоритма Рабина).
Электронная подпись. Принцип электронной подписи легко выводится из алгоритма RSA. Пусть нужно подписать текст T. Этот текст нудно «свернуть» в некое число y. Для свертки используют алгоритм хэширования. Теперь из уравнения (1.13) на основании секретного ключа получают подпись X. Число X и возвращается вместе с T и y в качестве подписи в документу Т. Не зная секретного ключа d (заменяющего фамилию), нельзя найти X. Проверяющий легко проверит (1.1), чтобы удостовериться, что X и y соответствуют друг другу. Заметим, что кто-либо может перехватить документ и подписать его своей подписью, если ему известно преобразование (1.13). Поэтому принятый «подделанный» документ должен быть «застрахован».
|
|
|
Для этого используется число e – открытый ключ подписавшего документ. Теперь очень легко проверить соотношение:
 .
.
Подобрать секретный ключ d к открытому ключу e практически невозможно.
Метод Диффи-Хеллмана.
Метод Диффи и Хеллмана является двухключевым. Каждый абонент в сети имеет два ключа: один секретный –  , второй открытый, вычисляемый по формуле
, второй открытый, вычисляемый по формуле
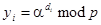 ,
,
где p – большое простое число (взаимно простое с  );
); 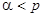 .
.
Число  выбирается так, чтобы числа
выбирается так, чтобы числа  ,
,  , …,
, …,  по модулю p давали некоторую перестановку чисел {1, 2, …, p -1}. Число
по модулю p давали некоторую перестановку чисел {1, 2, …, p -1}. Число  называется первообразным корнем p. Все абоненты публикуют свои открытые ключи
называется первообразным корнем p. Все абоненты публикуют свои открытые ключи  . Допустим, абоненты A и B хотят передать друг другу информацию. Тогда первый из них, например A, берет открытый ключ абонента B
. Допустим, абоненты A и B хотят передать друг другу информацию. Тогда первый из них, например A, берет открытый ключ абонента B  и вычисляет
и вычисляет
 .
.
Таким образом, оба абонента находят одно и то же число, которое они и используют в качестве ключа для обмена сообщениями. При этом секретные ключи абонентов остаются известными только им одним.
Алгоритм DES. Алгоритм DES (description encryption system) состоит в последовательности чередующихся операций подстановки и перемешивания. Алгоритм DES использует секретный ключ K. Пусть, например, блок данных есть  , а ключ
, а ключ  .
.
Подстановка есть сложение по модулю 2:

| 10010011 |
| 11001011 | |
| 01011000 |
Таким образом, операция подстановки непредсказуемым образом искажает исходные данные. Для восстановления исходных данных достаточно выполнить подстановку вторично:
|
|
|

| 01011000 |
| 11001011 | |
| 10010011 |
Операция перемешивания заключается в обмене местами двух блоков в соответствии с заранее составленными таблицами. Длина обмениваемых блоков одинакова, но варьирует от одного прохода к другому. Операция подстановки выполняется не над целым ключом, а над случайно выбираемой его частью. Эта случайно выбираемая часть сама определяется значением ключа. Одним из способов получения псевдослучайных чисел является следующий:
 . .
| (1.15) |
Здесь 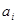 – псевдослучайное число, порожденное на шаге i. первоначально полагают, например,
– псевдослучайное число, порожденное на шаге i. первоначально полагают, например,  . В качестве константы C примем
. В качестве константы C примем
 , ,
| (1.16) |
где K – секретный ключ. Величина M как правило равна 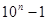 ; величина n равна числу разрядов генерируемого псевдослучайного числа. Например, пусть
; величина n равна числу разрядов генерируемого псевдослучайного числа. Например, пусть  ,
,  ,
,  ,
,  ,
,  :
:
 ,
,
 ,
,
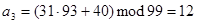 ,
,
 ,
,
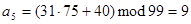 и т.д.
и т.д.
Порожденные псевдослучайные числа могут определять номера разрядов, выбираемых из ключа в формируемую часть для выполнения операции подстановки.
Для дешифрации принятой комбинации нужно знать ключ K и выполнять операции подстановки и перемешивания в обратном порядке
Сжатие информации
Сжатие по методу Д. Хаффмана
Метод сжатия Хаффмана является одним из лучших способов сжатия информации. Данный метод мы изложим на следующем примере. Пусть дана подлежащая сжатию последовательность из «0» и «1»:
| 010000101000101111001011. | (1.17) |
Разобьем эту последовательность на тройки разрядов и для каждой тройки подсчитаем, сколько раз она встречается в последовательности (рис. 1.13)
010’000’101’000’101’111’001’011
| 010 – 1 000 – 2 101 – 2 111 – 1 001 – 1 011 – 1 a) | 000 – 2 101 – 2 010 – 1 111 – 1 001 – 1 011 – 1 b) |
Рис. 1.13.
Упорядочим комбинации по частоте встречаемости (рис. 1.13b). Теперь «объединим» две последние комбинации на рис. 1.13b в одну и все комбинации снова переупорядочим по убыванию частоты встречаемости (рис. 1.14)
‘001-011’ – 2
000 – 2
101 – 2
010 – 1
111 – 1
Рис. 3.14.
Теперь снова объединим две последние комбинации в одну и проведем очередное упорядочение (рис. 1.15)
‘010-111’ – 2
‘001-011’ – 2
000 – 2
101 – 2
Рис. 1.15.
Дальнейший процесс объединения комбинаций выполним по аналогии (рис. 1.16, 1.17)
| ‘000-101’ – 2 ‘010-111’ – 2 ‘001-011’ – 2 Рис. 3.16. | ‘010-111-001-011’ – 4 ‘000-101’ – 4 Рис. 3.17. |
Теперь нарисуем дерево, схематически передающее реализованный нами способ объединения комбинаций (рис. 1.18)
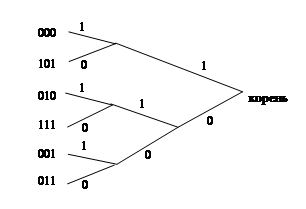
Рис. 1.18.
Для полученного дерева выполним движение с корневой вершины к исходным тройкам. При выходе из любого узла помечаем одно из двух ребер «1», а другое – «0» (рис. 1.18). Итак, запомним, что разметка выполняется при движении справа на лево по построенному дереву. Теперь новый код для любой из исходных троек получаем как комбинацию, сопоставляемую пути из корня в данную вершину. Получаем следующее соответствие исходных троек и новых комбинаций:
|
|
|
000 – 11
101 – 10
010 – 001
111 – 010
001 – 001
011 – 000
С учетом нового способа кодировки исходная последовательность (1.17) может быть переписана таким образом:
| 01111101110010001000. | (1.18) |
Длина последовательности (3.18) сократилась в сравнении с длиной (1.17) с 24 бит до 20 бит. Основной принцип кодирования Хаффмана состоит в том, что часто встречаемые комбинации кодируются более короткими последовательностями. Таким образом, общая длина последовательности оценивается как
 , ,
| (1.19) |
где  – число битов в i -ой комбинации,
– число битов в i -ой комбинации,
 – относительная частота встречаемости i -ой комбинации.
– относительная частота встречаемости i -ой комбинации.
Было замечено, хотя это и не обязательно верно во всех случаях, что длина кода Хаффмана комбинации  , как правило, не превосходит величину (–
, как правило, не превосходит величину (–  ). Так, в нашем примере относительная частота комбинации 000 составляет
). Так, в нашем примере относительная частота комбинации 000 составляет  . Ее код Хаффмана есть 11 (длина этого кода равна 2). Имеем
. Ее код Хаффмана есть 11 (длина этого кода равна 2). Имеем
 (что справедливо).
(что справедливо).
Таким образом, при кодировании Хаффмана результирующую длину кода можно ориентированно записать в виде
 . .
| (1.20) |
Кодирование Хаффмана модно применять повторно.
|
|
|


