 |
Лекция 28. Техника дифференцирования.
|
|
|
|
1. Обратные функции, их дифференцирование.
Функция 
называется обратной для функции 
, если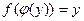 
. Обозначение: 
. Для того чтобы существовала функция обратная , соответствие, которое она задает должно быть не просто однозначным, а взаимно однозначным, т.е. 
. Область определения и область значений взаимно обратных функций меняются ролями, а их графики располагаются симметрично относительно прямой 
. Например, графики функций натурального логарифма 
и экспоненты 
.
Теорема 28.1. Если функция в точке 
имеет производную 
и существует обратная функция , то в соответствующей точке 
существует производная обратной функции и справедливы равенства: 
(28.1) и 
(28.1*).
Пример 1. Доказать: (1) 
, (2) 
.
Решение. (1) Функции 
и 
являются взаимно обратными, следовательно, по теореме 28.1 
. Выразим производную через аргумент 
. Из основного тригонометрического тождества 
, но поскольку 
и 
, то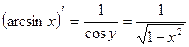 
.
(2) Функции 
и 
являются взаимно обратными 
. Выразим косинус через тангенс, используя основное тригонометрическое тождество: 
. Тогда 
.
Замечание. Формулы таблицы производных 
и 
доказываются аналогично.
2. Неявные функции, их дифференцирование.
Рассмотрим уравнение окружности (*) 
. Очевидно, что если одной из переменных, например , задавать значения, то значения второй переменной – 
будут определяться данным уравнением, т.е. у – значения некоторой функции от x, но явно эта зависимость не указана. В данном простом примере ее можно легко найти: 
, т.е. уравнение (*) задает две функции, такой способ задания называется неявным.
Сформулируем понятие неявной функции в общем виде. Будем говорить, что соотношение вида 
(28.2) неявно задает функцию 
(или 
), если 
(или 
). В тех случаях, когда из соотношения (28.2) невозможно выразить ни одну из переменных в явном виде, возникает проблема нахождения производной 
(или 
). Она решается с помощью следующего правила.
|
|
|
Чтобы найти производную функции (или ), которая неявно задана соотношением (28.2), дифференцируем обе части равенства по независимой переменной x (или y), считая другую переменную функцией от неё, применяя формулу дифференцирования сложной функции. В результате получаем уравнение относительно искомой производной, разрешая его, получаем значение производной в неявной форме.
Пример 2. Найти производные 
и 
неявно заданной функции 
.
Решение. Дифференцируем равенство, считая независимой переменной x и отмечая тот факт, что у зависит от х: 
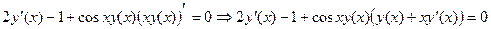. Раскроем скобки, оставим в правой части только те слагаемые, которые содержат искомую величину : 
. Выразим из этого уравнения искомую производную: 
или, убирая обозначение аргумента функции 
, 
. Отметим, что и производная задана неявно.
Чтобы найти проделаем то же самое, считая х функцией независимой переменной у:
.
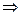
Прием логарифмического дифференцирования основан на том, что явно заданную функцию сначала логарифмируют по основанию e (фактически переходят к неявному заданию), а потом дифференцируют.Этот приемиспользуют в том случае, когда предварительное дифференцирование приводит к упрощению процесса дифференцирования, в частности, для вычисления производной 1) сложной степенно-показательной функции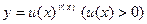 
, 2) произведения большого числа сомножителей.
Пусть нужно найти производную функции 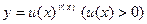. Прологарифмируем это равенство: 
. Дифференцируем полученную неявную функцию по переменной x: 
. Подставляя 
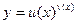, получаем: 
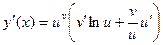или 
(28.2). Замечание. В формуле (28.2) первое слагаемое представляет собой производную степенной функции (
), а второе – производную показательной функции (
).
Пример 3. Найти производную функции 
.
Решение. Прологарифмируем функцию: 
. Дифференцируем обе части равенства по x: 
. Выразим из этого уравнения производную 
или
|
|
|
.
Пример 4. Найти производную функции 
.
Решение. Непосредственное применение формулы дифференцирования частного затруднительно, т.к. числитель и знаменатель являются произведениями 2-х функций. Можно считать, что функция представляет собой произведение 4-х сомножителей, которое после дифференцирования превращается в сумму натуральных логарифмов, что упрощает дифференцирование. Итак, 
. Откуда 
.
Используя прием логарифмического дифференцирования, легко доказать формулы таблицы производной: и . Если 
, то 
. Аналогично, 
.
Замечание. Формулу дифференцирования показательной функции можно доказать, воспользовавшись правилом дифференцирования обратной функции.
|
|
|
