 |
Лекция 30. Теоремы о дифференцируемых функциях.
|
|
|
|
Теорема 30.1 (Ферма). Пусть функция 
определена в окрестности точки 
, достигает в этой точке наибольшего или наименьшего значения. Если в точке существует производная, то 
.
Доказательство. Допустим, что в точке функция достигает своего наибольшего значения, т.е. 
и 
из некоторой окрестности этой точки. Приращение функции в точке 
при любом 
с условием, что 
находится в указанной окрестности. Тогда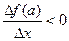 
при 
, следовательно, 
(1), при 
(1*). По условию теоремы производная 
существует, следовательно, её значение (по определению) не зависит от того, каким образом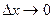 
. Таким образом, из неравенств (1) и (1*) следует 
.
В случае, когда 
– наименьшее значение, доказательство проводится аналогично, но 
.
С геометрической точки зрения теорема Ферма утверждает, что в точках, где функция достигает наибольшего или наименьшего значения касательная (если она существует) параллельна оси абсцисс (ОХ) (см. рис.1).
Теорема 30.2 (Ролля). Если функция 1) непрерывна на отрезке 
, 2) дифференцируема в интервале 
, 3) на концах отрезка принимает равные значения, т.е. 
, то в интервале существует (по крайней мере, одна) точка 
, в которой производная обращается в нуль, 
.
Доказательство. Поусловию 1) функция непрерывна на отрезке, следовательно, достигает там наибольшего значения – 
и наименьшего значения – 
(3) для 
. Возможны два случая: (а) оба значения функция принимает в конечных точках отрезка, (б) хотя бы одно из них достигается внутри отрезка. Рассмотрим случай (а). Пусть 
. Тогда из условия и неравенства (3) следует, что функция 
– константа 
. В этом случае теорема доказана. Если одно из значений M или m принимает во внутренней точке с, допустим 
, то по теореме Ферма , т.к. производная в этой точке существует (см. условие 2) теоремы Роля).
|
|
|
С геометрической точки зрения теорема Ролля означает, чтов некоторой внутренней точке интервала, где функция удовлетворяет теореме, касательная к графику параллельна оси Ох (см. рис.2).
Замечание 1. Иногда условие (3) в теореме Ролля формулируют в частном виде 
(это равносильно параллельному смещению оси Ох). В этом случае содержание теоремы кратко формулируют так: «между двумя нулями функции обязательно существует нуль её производной».
Замечание 2. Каждое из условий (1)–(3) теоремы Ролля существенно, т.е. при отбрасывании хотя бы одного из них заключение теоремы не выполняется.
Пример 1. Для функции 
производная 
, хотя не выполняется только условие 3) 
теоремы 30.2.
Пример 2. Для непрерывной функции 
, которая на концах отрезка принимает равные значения 
, но 
не существует (не выполняется условие 2) теоремы Роля) производная 
.
Пример 3. Для функции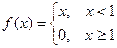 
на отрезке 
не выполняется только условие непрерывности (на правом конце, при 
) и 
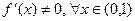
Теорема 30.3 (Лагрангжа). Если функция 1) непрерывна на отрезке , 2) дифференцируема в интервале , то в интервале существует (по крайней мере, одна) такая точка , что выполняется равенство:
. (30.1)
Формула (30.1) называется формулой конечных приращений или формулой Лагранжа.
Доказательство. Рассмотрим вспомогательную функцию 
. Для любого действительного числа 
функция 
непрерывна на отрезке , т.к. является суммой непрерывных функций (см. условие 1), и существует производная 
, т.е. дифференцируема в интервале . Покажем, что можно найти такое значение , что 
. 
(1).
Таким образом, при выбранном значении функция удовлетворяет всем условиям теоремы Ролля, следовательно, в интервале существует точка 
, в которой 
. Теорема доказана.
С геометрической точки зрения теорема Лагранжа утверждает, чтов некоторой внутренней точке интервала, где функция удовлетворяет теореме, касательная к графику параллельна хорде 
, которая стягивает дугу графика на отрезке , т.е. 
(см. рис.3). Действительно, 
, но производная в точке c равна угловому коэффициенту касательной, значение , определенное равенством (1) – это угловой коэффициент хорды .
|
|
|
Теорема Лагранжа и формула Лагранжа часто используются в других разделах математического анализа.
Теорема 30.4 (Коши). Если функции 
и 
1) непрерывны на отрезке , 2) дифференцируемы в интервале , 3) 
для 
, то в интервале существует (по крайней мере, одна) такая точка , что выполняется равенство:
. (30.2)
Формула (30.) называется формулой Коши.
Доказательство. Рассмотрим вспомогательную функцию 
. Для любого действительного числа функция непрерывна на отрезке , т.к. является суммой непрерывных функций (см. условие 1), и существует производная 
, т.е. дифференцируема в интервале . Покажем, что можно найти такое значение , что . 
. Следовательно, 
(*), если 
Однако из равенства 
по теореме Роля следует, что 
– противоречие с условием 3) теоремы 30.4. При выбранном значении функция 
удовлетворяет всем условиям теоремы Ролля. Значит, в интервале существует точка , в которой 
. Теорема доказана.
Замечание. Теорему Лагранжа можно рассматривать как частный случай теоремы Коши, полагая 
Теорему Коши нельзя доказывать, применяя теорему Лагранжа отдельно к каждой функции 
, т.к. для каждой из них существует точка, где выполняется равенство (30.1), но они могут не совпадать.
|
|
|
