 |
Построение числового эквивалента или взаимно-однозначного соответствия. (Ж.Пиаже, А.Шеминьска, 1952).
|
|
|
|
Цель: выявление сформированности логических действий установления взаимно-однозначного соответствия и сохранения дискретного множества.
Оцениваемые УУД: логические универсальные действия.
Возраст: ступень предшкольного образования (6.5 – 7 лет.
Форма и ситуация оценивания: индивидуальная работа с ребенком.
Материалы: 12 красных и 12 синих фишек (или 12 яиц и 12 подставочек для яиц)
Методика проведения: 7 красных фишек (или подставочек для яиц) выстраивают в один ряд (на расстоянии 2 сантиметров друг от друга).
Пункт 1.
Испытуемого просят положить столько же (такое же количество, ровно столько) синих фишек (или яиц), сколько красных (или подставочек для яиц)- не больше и не меньше. Ребенку позволяют свободно манипулировать с фишками, пока он не объявит, что окончил работу. Затем психолог спрашивает: «Что у тебя получилось? Здесь столько же синих фишек, сколько красных? Как ты это узнал? Ты мог бы это объяснить еще кому-нибудь? Почему ты думаешь, что фишек поровну?» К следующему пункту приступают после того, как ребенок установит правильное взаимно-однозначное соответствие элементов в двух рядах. Если это ребенку не удается, психолог сам устанавливает фишки во взаимно-однозначном соответствии и спрашивает у испытуемого, поровну ли фишек в рядах. Можно в качестве исходного момента задачи использовать и неравное количество элементов, если на этом настаивает ребенок.
Пункт 2.
Испытуемого просят сдвинуть красные фишки (или подставки для яиц) друг с другом так, чтобы между ними не было промежутков (если необходимо, психолог сам это делает), затем ребенка спрашивают: «А теперь поровну красных и синих фишек (подставочек для яиц)? Как ты это узнал? Ты мог бы это объяснить?». Если испытуемый говорит, что теперь не поровну, его спрашивают: «Что надо делать, чтобы снова стало поровну?» Если испытуемый не отвечает, психолог задает такой вопрос: «Нужно ли нам добавлять сюда несколько фишек (указывает на ряд, где, по мнению испытуемого, фишек меньше)?» Или задается такой вопрос: «Может быть, мы должны убрать несколько фишек отсюда (указывая на ряд, где, по мнению ребенка, их больше)?»
|
|
|
Для того, чтобы оценить уверенность ответов ребенка, психолог предлагает контраргумент в виде вымышленного диалога: «А знаешь, один мальчик мне сказал… (далее повторяются слова испытуемого), а другой не согласился с ним и сказал…». Если ребенок не меняет своего ответа, психолог может пойти еще дальше: «Этот мальчик сказал, что фишек поровну, потому что их не прибавляли и не убавляли. Но другой мальчик сказал мне, что здесь их больше, потому что этот ряд длиннее… А ты как думаешь? Кто из них прав?». Если испытуемый меняет свои первоначальные ответы, несколько подпунктов задачи повторяются. (В этой и других задачах на сохранение количества используются одни и те же контраргументы, поэтому мы их специально не описываем).
Критерии оценивания:
- умение устанавливать взаимно-однозначное соответствие
- сохранение дискретного множества.
Уровни сформированности логических действий:
- Отсутствует умение устанавливать взаимно-однозначное соответсвие. Отсутствует сохранение (после изменения пространственного расположения фишек ребенок отказывается признать равенство множеств фишек различных цветов).
- Сформирована операция установления взаимно-однозначного соответствия. Нет сохранения дискретного множества.
- Сформирована операция установления взаимно-однозначного соответствия. Есть сохранение дискретного множества, основанное на принципе простой обратимости, компенсации или признании того, что мы «ничего не прибавляли и не убавляли».
Проба на определение количества слов в предложении
|
|
|
(С.Н.Карпова)
Цель: выявление умения ребенка различать предметную и речевую действительность.
Оцениваемые УУД: знаково-символические познавательные действия, умение дифференцировать план знаков и символов и предметный план.
Возраст: ступень предшкольного образования (6.5 – 7 лет)
Форма и ситуация оценивания: индивидуальная беседа с ребенком.
Ребенку зачитывают предложение и просят назвать, сколько слов в предложении и назвать их.
- Скажи, сколько слов в предложении?
- Назови первое слово, второе …
Предлагаются предложения:
Маша и Юра пошли в лес.
Таня и Петя играют в мяч.
Критерии оценивания:
- Ориентация на речевую действительность
Уровни развития знаково-символических действий:
1- Ориентация на предметную действительность, нет осознания особого существования речевой действительности как знаково-символической. Дети дают неправильный ответ, ориентируются на предметную действительность, выделяют слова, перечисляя существительные-предметы.
2- Неустойчивая ориентация на речевую дейстивтельность. Дети дают частично верный ответ, правильно называют слова, но без предлогов и союзов.
3- Ориентация на речевую действительность как самостоятельную, дифференциация знаково-символическоого и предметоного планов. Дети дают частично верный (называют все слова, пропустив или предлог или союз) или полностью правильный ответ.
Методика «Кодирование»
(11 субтест теста Векслера в версии А.Ю.Панасюка, 1976)
Цель: выявление умения ребенка осуществлять кодирование с помощью символов.
Оцениваемые УУД: знаково-символические действия – кодирование (замещение); регулятивное действие контроля.
Возраст: предшкольная ступень (6.5 -7 лет).
Форма: индивидуальная или групповая работа с детьми.
Ситуация оценивания: ребенку предлагают в течение 2 минут осуществить кодирование, поставив в соответствие определенному изображению условный символ. Задание предполагает тренировочный этап (введение инструкции и совместную пробу с психологом). Далее предлагается продолжить выполнение задание, не допуская ошибок, как можно быстрее.
|
|
|
Критерии оценивания:
- количество допущенных при кодировании ошибок;
- число дополненных знаками объектов.
Уровни сформированности действия замещения:
- Ребенок не понимает или плохо понимает инструкции. Выполняет задание правильно на тренировочном этапе и фактически сразу же прекращает или делает много ошибок на этапе самостоятельного выполнения. Операция кодирования не сформирована.
- Ребенок адекватно выполняет задание кодирования, но допускает достаточно много ошибок (до 25% от выполненного объема), либо работает крайне медленно.
- Сформированность действия кодирования (замещения). Ребенок быстро понимает инструкцию, действует адекватно. Количество ошибок незначительно.
Диагностика особенностей развития поискового планирования (методика А.З.Зака)
Цель: выявление сформированности действия поискового планирования как умения разрабатывать программу выполнения действий для достижения поставленной цели.
Оцениваемые УУД: регулятивные действия планирования и контроля, логические действия анализа, синтеза, установления аналогий.
Возраст: ступень начального обучения (9-11 лет).
Форма и ситуация оценивания: групповая и индивидуальная форма.
Далеко не всегда имеет место разработка программы действий.
В этом случае каждое действие планируется и сразу же выполняется. Поэтому
последующие действия планируются только после выполнения предыдущих.
Такая форма планирования квалифицируется как последовательно-частичное
планирование. В других случаях разрабатываются и сопоставляются разные варианты всей последовательности требуемых действий. При этом предыдущие действия выполняются лишь после того, как будут намечены все последующие действия. Такая форма планирования квалифицируется как предварительно-целостное планирование.
Для диагностики поискового планирования можно использовать тип задач, в которых для достижения результата требуется выполнить ряд действий. В этом случае можно будет различить уровни развития планирования у детей в зависимости от того, какое количество действий (до выполнения) способен наметить ребенок.
|
|
|
К такому типу относятся задачи «слон — ладья». Смысл их заключается в том, чтобы некоторое расположение объектов преобразовать в другое за определенное количество действий по определенным правилам.
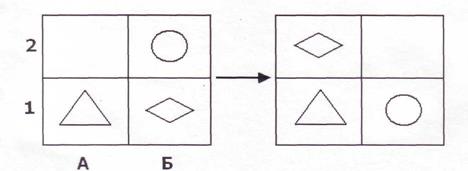
Например, расположение цифр в квадрате «А» нужно преобразовать в расположение тех же цифр, указанное в квадрате «Б» за два действия по следующему правилу: любая цифра за одно действие может переместиться прямо или наискось только в соседнюю свободную клетку:

В данной задаче первое действие состоит в перемещении по прямой (ходом шахматной фигуры «ладья») цифры «1», а второе действие связано с перемещением в соседнюю свободную клетку наискось (ходом шахматной фигуры «слон») цифры «2». Усложнение условий планирования при решении
таких задач связано как с увеличении числа требуемых операций, так и с возрастанием числа клеток и числа перемещающихся объектов.
Групповое диагностическое исследование для определения различий в планировании у младших школьников строится следующим образом.
1. Психолог, проводящий диагностическое занятие, приходит в класс с
комплектом бланков и с чистыми листами бумаги для записи решения задач:
на этих листах каждый ребенок пишет свою фамилию и ставит дату
проведения занятия.
2. Пока дети подписывают чистые листы, психолог чертит на классной доске
два четырехклеточных квадрата:

3. Детям говорится: «Сегодня мы будем решать интересные задачи.
Посмотрите на эти два квадрата. Каждая клетка в квадрате имеет свое
название, которое состоит из буквы и цифры. Эта клетка (следует указать
нижнюю левую клетку) называется А1, а эта клетка (указывается правая
нижняя) называется Б1, а эти две клетки (верхние две клетки квадрата)
называются А2 и Б2».
4. «Теперь решим такую интересную задачу. Сначала три фигурки — круг,
треугольник и ромб — были в таких клетках», — психолог рисует указанные
фигурки:

«А потом фигурки поменяли свои места и оказались в других клетках», — психолог рисует фигурки в правом квадрате:
|
«Нам нужно угадать, узнать, какие два действия, два перемещения сделали фигурки, чтобы попасть в другие клетки. Чтобы решить эту задачу, нужно знать правило: любая фигурка может перемещаться только в свободную соседнюю клетку прямо или наискось. Кто скажет, какое было первое перемещение, какая фигурка первая передвинулась в свободную клетку?... Правильно, первое действие сделал ромб: из клетки Б1 он передвинулся наискось в клетку А2. Запишем это действие, используя названия клеток:

А какое будет второе действие?... Правильно, второе действие выполнил круг. Он передвинулся из клетки Б2 прямо в клетку Б1. Запишем второе действие рядом с первым:
|
|
|
1)Б1 ->вА2;2)Б2-*Б1.
5. Вот так решаются задачи на перемещение фигурок из одних клеток в другие.
Сейчас я раздам бланки с условиями задач, которые вы будете сегодня
решать», — психолог раздает бланки, в каждом из которых даны 12 задач.
6. «Давайте посмотрим на лист с задачами. На самом верху есть задачи №1 и
№2. В них нужно отгадать, найти два действия. Затем идут задачи №3 и №4
— в них нужно найти 3 действия. Далее в задачах №5 и №6 нужно найти 4
действия, в задачах №7 и №8 нужно найти 5 действий, в задачах №9 и №10
— 6 действий, в задачах №11 и №12 — 7 действий.
7. Теперь попробуйте сами решить задачу №1 в два действия. Помните наше
правило: фигурки перемещаются прямо и наискось в свободную клетку.
Подумайте, как перемещались фигурки: какая фигурка передвинулась
первой, какая передвинулась второй. Потом запишите эти два действия также, как мы это делали на доске: сначала номер задачи, потом первое действие и второе».
8. Дети решают задачу №1, психолог проходит по рядам и контролирует
правильность записи решения.
9. «Давайте проверим теперь решение задачи №1», — психолог на доске
рисует условие задачи № 1:

Кто скажет решение?... Верно, первое действие сделал круг, второе — треугольник: №1. 1) А2 —> Б1; 2) А1 —> А2.
10. Теперь решайте задачу №2, — в ней тоже нужно найти 2 действия». Дети
решают задачу, психолог контролирует работу детей.
11. «Давайте проверим решение задачи №2», — психолог рисует на доске
условие задачи:

12.«Кто скажет решение этой задачи? Верно, первое действие: треугольник переместился из клетки Б1 в В1. Запишем эти два действия:
№2. 1)В1 →Б2;2)Б1→ В1.
13.Вот так решаются и записываются действия в наших задачах. Теперь сами и уже без проверки решайте все задачи подряд: №№3, 4 и т.д., кто сколько успеет. Только помните правило: фигурки перемещаются прямо и наискось в соседнюю свободную клетку. На бланке с задачами ничего писать нельзя: ни точки, ни линии. Нужно просто смотреть на условия задач и думать, какие перемещения сделали фигурки из одних клеток в другие». Последнее требование, — не касаться бланка ручкой или карандашом, — принципиально важно для диагностики планирования, поскольку проверяется развитие способности действовать «в уме», в мысленном плане, в представлении, т.е. без фиксирования промежуточных результатов на бумаге, например, в виде точки на клетке с той или иной фигуркой или проведения линий, указывающих на возможные перемещения фигурок.
14.На инструктирование детей отводится (в зависимости от возраста) 10-15 минут, а на самостоятельное решение задач №№ 3 - 12 должно быть потрачено ровно 20 минут. По истечении этого времени бланки и листы с ответами (кто сколько успел решить) собираются.
Критерии и уровни оценки планирования:
1. протяженность последовательности действий (количество действий), спланированная ребенком.
Обработка результатов
Результаты решения задач, находящиеся на листах бумаги с фамилиями детей, можно обрабатывать, сверяясь с ключом, где представлены правильные действия к каждой задаче.
Диагностическое задание включает задачи двух видов. К первому относятся задачи, решение которых может быть достигнуто с помощью частичного планирования, — это задачи №№ 1 и 2, — поскольку выбор первого действия однозначен, и его наметка и выполнение не связаны с наметкой и выполнением второго действия.
Ко второму виду относятся задачи, решение которых предполагает осуществление целостного планирования, это задачи № 3 - 12, поскольку выбор первого действия неоднозначен. Последнее означает, что правильный выбор первого действия влияет на возможность решить задачу за требуемое число действий, и поэтому наметку первого действия следует проводить одновременно с наметкой всех остальных действий.
Уровни планирования:
1 - успешное решение задач № 3 и №4
2 – успешное решение задач №5 и №6
3 – успешное решение задач №6 и №7
4 – успешное решение задач №9 и № 10
5 – успешное решение задач № 11 и № 12
В целом, таким образом, проведение группового диагностического занятия с детьми 7-10 лет позволяет выделить тех, кто обладает либо только частным планированием (при решении лишь двух первых задач), либо разными уровнями развития целостного планирования, — при успешном решении, соответственно, задач №№ 1 - 4; 1 - 6; 1 - 8; 1 - 10; 1 - 12.
|
|
|


