 |
Теорема 1. (Об обратной матрице)
|
|
|
|
Введение
Обозначения
Î - знак принадлежности;
 – пустое множество;
– пустое множество;
ï,: - “такой, что”;
Þ - “следует”;
Û - “тогда и только тогда”;
N - множество натуральных чисел;
Z - множество целых чисел;
R - множество действительных чисел;
Q - множество рациональных чисел.
Кванторы:
" - “для любого”;
$ - “существует”.
Глава 1. Линейная алгебра
§1. Матрицы. Действия над ними.
Опр.1. Таблица вида 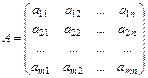 =
=  =
=  наз. матрицей размера m
наз. матрицей размера m  n, m - число строк, n - столбцов,
n, m - число строк, n - столбцов,  наз. элементами матрицы A
наз. элементами матрицы A  .
.
В дальнейшем строки и столбцы будем наз. рядами.
Опр.2. При m=n -матрица наз. квадратной порядка n:  .
.
ПР. Некоторая компания в перерабатывающей промышленности располагает данными о своих продажах на протяжении года, сгруппированными по видам изготовляемой продукции и районам сбыта.
| Вид |  Районы продажи Районы продажи
| ||
| продукции | |||
 .
.
Опр.3. Пусть A =  ,
,  .
.

 =
=  ,
,  .
.
Опр.4. Нулевой матрицей наз. матрица О 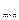 , все элементы которой равны 0.
, все элементы которой равны 0.
Опр.5. Единичной матрицей наз. квадратная матрица Е  , где
, где  . ПР.
. ПР. 

Опр.6. Суммой матриц A и B размера  наз. матрица
наз. матрица  :
:  ,
,  .
.
Опр.7. Произведением матрицы Aна число  наз. матрица
наз. матрица  :
:  ,
,  . ПР.
. ПР.
Опр.8. Операции сложения матриц и умножения матрицы на число наз. линейными операциями.
Свойства линейных операций (аналогичны свойствам операций над числами):
1) A+B=B+A; 2) 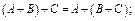
3)  ; 4)
; 4) 
5) 
Опр.9. Операция над матрицей A, при которой ее строки становятся столбцами с теми же номерами, наз. транспонированием. Обозначение  .
.
ПР.
Опр.10. Пусть  ,
,  .
.
Опр.11. Произведением матриц A и B наз. матрица  , элементы которой вычисляются по формуле
, элементы которой вычисляются по формуле
 ,
,  .
.
ПР.  ,
,  .
.  .
.
Замечание 1. Умножать матрицу А на матрицу В можно тогда и только тогда, когда число столбцов матрицы А равно числу строк матрицы В.
|
|
|
Замечание 2. В общем случае  . Если же
. Если же 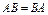 , то
, то
матрицы наз. перестановочными.
Свойства умножения матриц. (Предполагаем, что матрицы А, В, С имеют размеры, позволяющие производить указанные действия.)
1)  , где
, где  ; 2)
; 2) 
3) 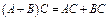 ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
Определители.
Опр.1. Квадратной матрицей порядка n наз. матрица А размера  .
.
Опр.2. Определителем квадратной матрицы  первого порядка наз. число
первого порядка наз. число 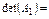
 =
=  .
.
Опр.3. Определителем квадратной матрицы  называется
называется 
Воспользуемся методом математической индукции.
Пусть определен определитель (n-1)-го порядка.
Опр.4. Минором  элемента
элемента 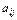 квадратной матрицы
квадратной матрицы  наз. определитель матрицы, полученной из данной вычеркиванием i -й строки и j -го столбца.
наз. определитель матрицы, полученной из данной вычеркиванием i -й строки и j -го столбца.
ПР. 
Опр.5. Алгебраическим дополнением  элемента
элемента 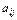 квадратной матрицы
квадратной матрицы  наз. число
наз. число  .
.
ПР.  .
.
Опр.6. Определителем квадратной матрицы порядка n наз. число, которое ставится ей в соответствие по формуле:

 . Такое вычисление определителя наз. разложением по первой строке.
. Такое вычисление определителя наз. разложением по первой строке.
ПР.  =
=  = разложим по 1-й строке= =
= разложим по 1-й строке= = 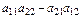 .
.
ПР. 
 = разложим по 1-й строке =
= разложим по 1-й строке =

ПР.  = – 286,
= – 286,  .
.
Свойства определителей. Пусть  .
.
1) Сумма произведений элементов любого ряда определителя на их алгебраические дополнения не зависит от номера ряда и равна этому определителю:
 .
.
2) 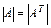 .
.
3) При перестановке двух параллельных рядов определитель меняет знак.
ПР. 
4) Если матрица А имеет два пропорциональных параллельных ряда, то  =0.
=0.
ПР.  .
.
5) Общий множитель элементов ряда можно выносить за знак определителя.
ПР. 
6) Определитель, имеющий нулевой ряд, равен нулю.
7) Величина определителя не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого параллельного ему ряда, умноженные на число k (док. сам.).
ПР.  .
.
8) Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов другого параллельного ему ряда равна нулю (док. сам.)
|
|
|
9) Пусть  и
и  – определители, различающиеся элементами только одного ряда. Тогда их сумма равна определителю, у которого указанный ряд состоит из сумм соответствующих элементов определителей
– определители, различающиеся элементами только одного ряда. Тогда их сумма равна определителю, у которого указанный ряд состоит из сумм соответствующих элементов определителей  и
и  .
.
10)  .
.
Замечание 2. Из свойств следует, что определитель удобно вычислять, преобразовав предварительно его так, чтобы в каком-либо ряду получились нули (если все нули, то определитель =0).
ПР. 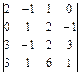 =0;
=0;
Опр.7. Квадратная матрица наз. вырожденной, если ее определитель равен нулю, в противном случае – невырожденной.
§3 Обратная матрица.
Пусть  .
.
Опр.1. О братной к матрице А наз. такая матрица  , что
, что
 .
.
Теорема 1. (Об обратной матрице)
Если матрица  - невырожденная, то она имеет обратную, которую можно найти по следующей формуле:
- невырожденная, то она имеет обратную, которую можно найти по следующей формуле:
 ,
,
где 
 - алгебраические дополнения элементов
- алгебраические дополнения элементов  исходной матрицы А
исходной матрицы А  .
.
Док-во. Пусть  . Покажем, что
. Покажем, что  .
.
Пусть 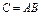 , тогда
, тогда  =
=
=  =
= 
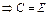 .
.
Аналогично проверяется, что  . Ч.т.д.
. Ч.т.д.
Следствие. Для невырожденной матрицы  обратная матрица имеет вид
обратная матрица имеет вид  .
.
ПР.1.  ,
,  . Проверка!
. Проверка!
ПР.2. 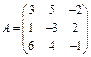 ,
,  .Проверка!
.Проверка!
Замечание. Если  , то
, то  не существует.
не существует.
Ранг матрицы.
Рассмотрим матрицу  . Пусть
. Пусть 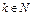 и
и  .
.
Опр.1. Выделимв матрице Аk строк и k столбцов. Определитель порядка k, порожденный элементами, стоящими на пересечении выделенных строк и столбцов, наз. минором k-го порядка матрицы 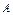 и обозначается
и обозначается  .
.
ПР.  .
. 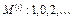 ,
,

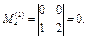
Опр.2. Наибольший порядок ненулевого минора матрицы А наз рангом этой матрицы. Обозначение: 
Очевидно, что 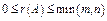 .
.
Замечания:
1)  . Во всех остальных случаях
. Во всех остальных случаях 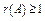 ;
;
2)  ;
;
3) 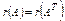 ;
;
4) добавление или вычеркивание нулевого ряда не меняет ранга матрицы.
Опр.3. Базисным минором называется минор, не равный нулю, порядок которого совпадает с рангом матрицы.
Опр.4. Элементарными преобразованиями матрицы называют:
1) умножение некоторого ряда на число, отличное от нуля;
2) перестановка двух параллельных рядов.
3) прибавление к одному ряду любого другого, параллельного ему, умноженного на какое-либо число.
|
|
|


