 |
Теорема 2. (Об элементарных преобразованиях матрицы)
|
|
|
|
Элементарные преобразования не меняют ранга матрицы.
Опр.5. Минором, окаймляющим минор  матрицы А, наз. минор
матрицы А, наз. минор  , содержащий минор
, содержащий минор  .
.
Можно выделить два метода отыскания ранга матрицы:
а) с помощью окаймляющих миноров: если в матрице А имеется минор 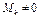 , а все окаймляющие его миноры
, а все окаймляющие его миноры 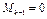 , то ранг матрицы равен k;
, то ранг матрицы равен k;
б) с помощью элементарных. преобразований приводим матрицу к виду трапеции.
ПР. 
 .
.
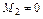 , все
, все 
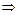
Системы линейных алгебраических уравнений.
Опр.1. Системой m линейных уравнений с n неизвестными наз. система вида:
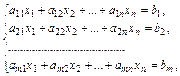 (1),
(1),
где 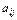 -коэффициенты при неизвестных
-коэффициенты при неизвестных 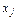 ,
, 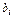 - свободные коэффициенты (свободные члены),
- свободные коэффициенты (свободные члены), 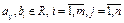 .
.
Опр.2. Система (1) наз. однородной при 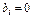 ,
,  .
.
Опр.3. Упорядоченный набор чисел 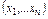 наз. решением системы (1), если при подстановке этих чисел вместо неизвестных в систему каждое уравнение обращается в верное равенство.
наз. решением системы (1), если при подстановке этих чисел вместо неизвестных в систему каждое уравнение обращается в верное равенство.
Опр.4. Решить систему (1) – это значит либо найти все ее решения, либо установить, что их нет.
Опр.5. Система(1) наз. совместной, если она имеет хотя бы одно решение (в противном случае - несовместной).
Опр.6. Система (1) наз. определенной, если имеет единственное решение, и неопределенной, если имеет бесконечное множество решений.
Опр.7. Две системы наз. эквивалентными или равносильными, если множества их решений совпадают.
Опр.8. Элементарными преобразованиямисистемы (1) наз. следующие:
1) прибавление к одному уравнению любого другого уравнения, умноженного на какое-либо число;
2) умножение какого-либо уравнения на число, отличное от нуля;
3) перестановка уравнений системы.
Теорема 2. (Об элементарных преобразованиях системы)
Элементарные преобразования системы линейных уравнений приводят ее к эквивалентной.
Система (1) может быть записана в матричном виде: 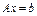 , где
, где
|
|
|
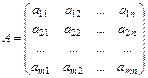 наз. матрицей системы,
наз. матрицей системы,
вектор 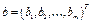 наз. столбцом свободных членов,
наз. столбцом свободных членов,
вектор 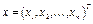 наз. столбцом неизвестных.
наз. столбцом неизвестных.
Опр.9. Расширенной матрицей системы (1) наз. матрица
 .
.
Теорема 3. (Теорема Кронекера-Капелли)
Система (1) совместна в том и только в том случае, когда ранг матрицы системы равен рангу расширенной матрицы:
 .
.
§ 6 Методы решения систем линейных уравнений.
Метод обратной матрицы
Пусть в системе (1) т=п. Тогда матрица системы А является квадратной, и можно вычислить ее определитель. Если 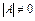 , то матрица А имеет обратную
, то матрица А имеет обратную  , и система
, и система 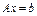 может быть решена следующим способом:
может быть решена следующим способом:
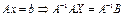

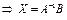 .
.
ПР. 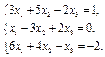
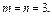
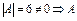 имеет
имеет  .
.

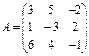 ;
; 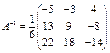 (см. §3),
(см. §3),
 ,
, 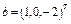
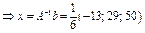 ,
, 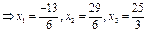 .
.
6.2. Метод Крамера.
Для (1) при условии m=n и 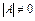 введем обозначения:
введем обозначения:
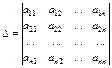 - определитель системы,
- определитель системы, 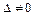
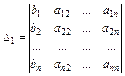 ,…,
,…, 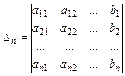 .
.
Теорема 4. (Формулы Крамера)
Если определитель системы 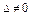 , то система
, то система 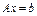 имеет единственное решение, вычисляемое при любом векторе b по формулам:
имеет единственное решение, вычисляемое при любом векторе b по формулам:
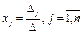 . (2)
. (2)
Формулы (2) наз. формулами Крамера.
Замечание:
1) если 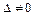 , то система имеет единственное решение;
, то система имеет единственное решение;
2) если  и хотя бы один из
и хотя бы один из 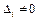 , то система не имеет решения;
, то система не имеет решения;
3) если  и все
и все 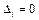 , то система либо имеет бесконечное множество решений, которое можно найти с помощью метода Гаусса (см. п.6.3), либо не совместна.
, то система либо имеет бесконечное множество решений, которое можно найти с помощью метода Гаусса (см. п.6.3), либо не совместна.
ПР. 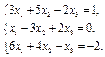
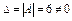 .
.
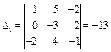 ;
; 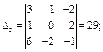
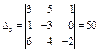 .
.
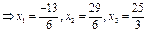 . Проверка.
. Проверка.
Метод Гаусса.
Идея метода Гаусса состоит в том, чтобы с помощью элементарных преобразований строк расширенной матрицы 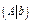 системы уравнений (1) и перестановки столбцов матрицы А привести матрицу
системы уравнений (1) и перестановки столбцов матрицы А привести матрицу 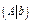 к следующему виду
к следующему виду
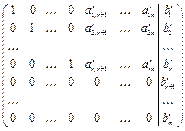 . (3)
. (3)
Тогда 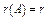 .
.
Если среди чисел 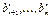 есть хотя бы одно, отличное от нуля, то
есть хотя бы одно, отличное от нуля, то 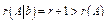 . Следовательно, система (1) не совместна по теореме Кронекера-Капелли.
. Следовательно, система (1) не совместна по теореме Кронекера-Капелли.
Если  , то
, то  и, следовательно, система (1) совместна. Матрица (3) задает систему, эквивалентную (1):
и, следовательно, система (1) совместна. Матрица (3) задает систему, эквивалентную (1):
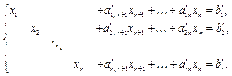
Переменные, отвечающие единичной подматрице 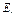 матрицы А, т.е.
матрицы А, т.е.  , наз. базисными, остальные – небазисными или свободными.
, наз. базисными, остальные – небазисными или свободными.
Опр. Решение системы (1), в котором все небазисные переменные равны нулю, наз. базисным.
|
|
|
Замечание. Для однородной системы  и
и  , т.е. однородная система всегда совместна и решение
, т.е. однородная система всегда совместна и решение 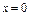 у нее есть всегда. Такое решение называется тривиальным.
у нее есть всегда. Такое решение называется тривиальным.
ПР. 

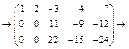
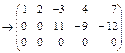 =
= 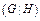 .
. 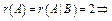
система совместна; 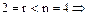 система имеет бесконечно много решений;
система имеет бесконечно много решений;
 ,
,  - базисные неизвестные,
- базисные неизвестные,
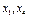 -свободные неизвестные.
-свободные неизвестные.
По виду 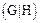 составляем систему, эквивалентную данной:
составляем систему, эквивалентную данной:

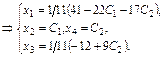
ПР. 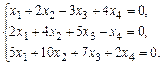
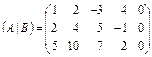
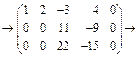
 =
= 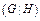 .
. 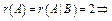
система совместна; 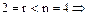 система имеет бесконечно много решений.
система имеет бесконечно много решений.
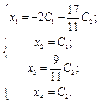
ПР. 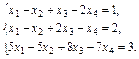
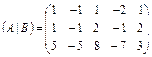
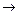

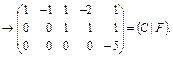

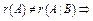
система несовместна, т. е. не имеет решения.
|
|
|


