 |
Отсечение нелицевых граней
|
|
|
|
Основной задачей при построении полноценного изображения является построение проекции на экран. Предположим, имеется некоторая модель, расположение вершин в пространстве которой заведомо известно. Для того чтобы вывести полноценный трехмерный объект на экран мы должны изобразить все его видимые грани. Для этого необходимо определить, какие из них находятся ближе к наблюдателю, а какие выпадают из поля зрения исключить их из процесса отрисовки, сэкономив при этом ресурсы системы. Один из самых быстрых способов проверки основан на определении направления нормали к грани.
Нормаль - это прямая, ортогональная (перпендикулярная) касательной прямой к некоторой кривой или касательной плоскости к некоторой поверхности (рис. 3). Большое значение при построении объектов имеет не сама нормаль, а ее вектор.

Рисунок 3
Вектором нормали к поверхности в данной точке является вектор, приложенный к данной точке и параллельный направлению нормали. Для каждой точки гладкой поверхности можно задать два нормальных вектора, отличающихся направлением. Если на поверхности можно задать непрерывное поле нормальных векторов, то говорят, что это поле задает ориентацию поверхности (то есть выделяет одну из сторон), а если же этого сделать нельзя, поверхность называют неориентируемой.
Предположим, существует объект, внутри которого камера (позиция наблюдателя) заведомо не окажется. Обычно такого рода объекты составляют большую часть или всю сцену. Тогда для каждой грани наблюдатель способен увидеть только одну ее сторону - лицевую. Грань - плоскость, она делит все 3D пространство на два полупространства. Таким образом, лицевую сторону видно только из одного полупространства, из того, в которое "смотрит" нормаль к этой грани, направленная из объекта. Проверив, в какое полупространство попадает камера, можно сразу определить, является ли грань лицевой (то есть, может ли камера увидеть лицевую сторону этой грани) и надо ли ее рисовать.
|
|
|
Пусть грань имеет вершины v1, v2, v3 и нормаль (nx,ny,nz). Тогда уравнение плоскости, в которой она лежит, будет иметь вид
*x+ny*y+nz*z+d = 0.
находим из того факта, что v1 в плоскости лежит:
*v1.x+ny*v1.y+nz*v1.z+d = 0,= -(nx*v1.x+ny*v1.y+nz*v1.z).
Функция nx*x+ny*y+nz*z+d принимает положительные значения по одну сторону от плоскости, отрицательные по другую и равна нулю на самой плоскости. Точка (v1.x+nx,v1.y+ny,v1.z+nz) лежит, очевидно, в том полупространстве, откуда грань видно. Значение функции (назовем ее функцией видимости) в этой точке равно
*(v1.x+nx)+ny*(v1.y+ny)+nz*(v1.z+nz)+d = nx*(v1.x+nx)+ny*(v1.y+ny)+nz*(v1.z+nz)-(nx*v1.x+ny*v1.y+nz*v1.z) = nx*nx+ny*ny+nz*nz > 0.
Таким образом, если значение функции в какой-то точке больше нуля, то грань из этой точки потенциально видна. Для построения изображение важен факт видимость грани из позиции камеры, а камера зафиксирована в точке (0,0,-dist). Таким образом, получаем, что грани, для которых
nz*dist-(nx*v1.x+ny*v1.y+nz*v1.z) < 0,
или, что равносильно,*dist+nx*v1.x+ny*v1.y+nz*v1.z > 0,
заведомо не видны и время на их обработку и отображение тратить не стоит.
Отдельного рассмотрения требует вопрос расчета нормали к граням. Точнее, как выбрать одну из двух нормалей, смотрящую из объекта. Обычно эта проблема решается еще на этапе построения 3D моделей - некоторые пакеты для 3D-моделирования заранее записывают вершины граней в порядке A-B-C так, чтобы векторное произведение BA*CA и было нормалью. Еще один способ - выбрать внутреннюю точку для объекта (либо вручную, либо взять его центр тяжести, либо любым другим способом - методов может быть придумано сколь угодно) и использовать ее: если для этой точки функция видимости положительна, то есть грань якобы видна, то необходимо поменять знак nx, ny и nz.
|
|
|
Рассмотрев метод, следует отметить, что для выпуклых объектов этот метод полностью решает задачу об удалении невидимых частей. Для невыпуклых же он позволяет быстро и просто сократить число граней, подлежащих дальнейшей проверке на видимость и, собственно, отрисовке.
Вращение
Вращение объекта в основном является изменением координат вершин, т.е. фактически заданием новых координат. В данном случае его можно реализовать довольно простым методом - вычислением новых координат, зная величину угла поворота, что сводится к решению ряда тривиальных тригонометрических задач.
Рассмотрим для примера поворот точки (x,y,z) относительно оси z. В этом случае z не изменяется вовсе, а (x,y) изменяются так же, как и при повороте на плоскости относительно начала координат. Рассмотрим, какие координаты получит точки A' в результате поворота A(x,y) на некоторый угол α.
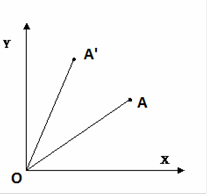
Рисунок 4
Пусть

Пусть угол AOx равен ᴪ, тогда из рисунка 4 видно, что
(ᴪ i) = x/r, sin(ᴪ) = y/r.
Угол A'OA равен по условию α.
Отсюда
x' = r*cos(α+ ᴪ) = r*(cos(α)*cos(ᴪ)-sin(α)*sin(ᴪ)) =
= (r*cos(ᴪ))*cos(α)-(r*sin(ᴪ))*sin(α) =
= x*cos(α)-y*sin (α))' = r*sin(α + ᴪ) = r*(cos(α)*sin(ᴪ)+sin(α)*cos(ᴪ)) =
= (r*cos(ᴪ))*sin(α)+(r*sin(ᴪ))*cos(α) =
= x*sin(α)+y*cos(α)
Рассматривая случай с трехмерным пространством, таким образом
' = x*cos(α)-y*sin(α)' = x*sin(α)+y*cos(α)
z' = z
Аналогично выводятся формулы и для других осей поворота (Ox, Oy). Поворот относительно произвольной оси, проходящей через начало координат, можно сделать с помощью этих поворотов - сделать поворот относительно Ox так, чтобы ось поворота стала перпендикулярна Oy, затем поворот относительно Oy так, чтобы ось поворота совпала с Oz, сделать собственно поворот, а затем обратные повороты относительно Oy и Ox. В результате чего соответственно получаем:
:=Y*cos(xv)-Z*sin(xv):=Y*sin(xv)+Z*cos(xv)
Здесь Y, Z это координаты вершины, а xv - угол поворота в градусах. Аналогично решаются задачи для поворота по оси X:
:=X*cos(yv)-Z*sin(yv):=X*sin(yv)+Z*cos(yv)
И, соответственно, по оси Z:
:=X*cos(zv)-Y*sin(zv):=X*sin(zv)+Y*cos(zv)
Важно отметить, что любая среда программирования работает с формой записи угла в радианах. Соответственно для любого значения в градусах необходимо выполнить преобразование - помножить значение в градусах на число Пи разделить на 180.
|
|
|


