 |
Ряды распределения, их виды, графическое изображение (полигон, гистограмма, кумулята)
|
|
|
|
В результате обработки и систематизации первичных статистических материалов получаются ряды цифровых статистических показателей, которые характеризуют отдельные стороны изучаемых явлений. Эти ряды называются статистическими.
Статистические ряды бывают двух видов: ряды распределения и ряды динамики (рис. 1).
Статистические ряды
Ряды распределения Ряды динамики
 |
Атрибутивные Вариационные
 |  |
Дискретные Непрерывные
(Интервальные)
Рисунок 1 – Виды рядов распределения
Ряды распределения – это ряды, которые характеризуют распределение единиц совокупности по какому-либо признаку (например, распределение производственного оборудования по видам и срокам службы). Ряд распределения состоит из двух элементов: вариант – значений группировочного признака 
и частот – число повторений отдельных вариантов значений признака.
Ряд распределения – группировка, в которой для характеристики групп, упорядоченно расположенных по значению признака, применяется только один показатель - численность групп.
Частоты, представленные в относительном выражении, называют частостями и обозначают 
.
Например, вместо абсолютного числа рабочих, имеющих определённый разряд, можно установить долю рабочих этого разряда. Частости могут быть выражены в долях единицы или в процентах. Замена частот частостями позволяет сопоставить вариационные ряды с различным числом наблюдений.
По характеру вариации различают дискретные и непрерывные признаки. Дискретные признаки отличаются друг от друга на некоторую конечную величину, то есть даны в виде прерывных чисел. Например, тарифный разряд рабочих, количество детей в семье, число рабочих на предприятии. Непрерывные признаки могут отличаться один от другого на сколь угодно малую величину и в определённых границах принимать любые значения. Например, заработная плата рабочих, стоимость основных фондов предприятия.
|
|
|
Атрибутивный ряд распределения образуется по качественному признаку (распределение рабочих по профессиям, машин – по маркам). Вариационный ряд распределения образуется по количественному признаку. Он состоит из вариант и частот. В дискретном ряде распределения отдельные варианты имеют определённые значения (распределение рабочих по разрядам). В тех случаях, когда число вариантов дискретного признака достаточно велико, а также при анализе вариации непрерывного признака, когда значения этого признака у отдельных единиц могут вообще не повторяться, строятся интервальные ряды распределения. Интервал указывает определённые пределы значений варьирующего признака и обозначается верхней и нижней границей интервала.
Различают ряды распределения с абсолютными, относительными и накопленными частотами. Накопленные частоты называют кумулятивными.
Если приведён вариационный ряд с неравными интервалами, то для правильного представления о характере распределения необходимо рассчитать плотность распределения. Плотность распределения – это количество единиц совокупности, приходящихся на единицу величины интервала группировочного признака. Различают абсолютную (
) и относительную (
) плотность:
,
,
где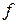 
– частота;
– удельный вес;
– размер интервала.
По форме ряды распределения бывают одно- двух- и многовершинными. Среди одновершинных распределений есть симметричные и асимметричные (скошенные), остро- и плосковершинные.
Графическое изображение рядов распределения облегчает их анализ и позволяет судить о форме распределения.
|
|
|
Для графического изображения дискретного ряда применяют полигон распределения. Полигон чаще всего используют для изображения дискретных рядов. Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами (xi,mi), где xi – варианты выборки и mi – соответствующие им частоты. Если полигон строят по данным интервального ряда, то в качестве абсцисс точек берут середины соответствующих интервалов.
Для построения полигона в прямоугольной системе координат в произвольно выбранном масштабе на оси абсцисс откладывают значения аргумента (варианты), а на оси ординат – значения частот. Масштаб выбирают такой, чтобы была обеспечена необходимая наглядность и желательный размер рисунка. Далее строят точки с координатами (xi,mi) и последовательно соединяют их отрезками прямой.
Рисунок 2 – Полигон распределения
Для графического изображения интервальных вариационных рядов применяются гистограммы. Она строится так: на оси абсцисс откладываются равные отрезки, которые в принятом масштабе соответствуют величине интервалов вариационного ряда. На отрезках строят прямоугольники, площади которых пропорциональны частотам (или частностям) интервала.
Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединяются отрезками прямых. Две крайние точки прямоугольников замыкаются по оси абсцисс на середины интервалов, в которых частоты (частности) равны нулю. При построении гистограммы для вариационного ряда с неравными интервалами следует по оси ординат наносить показатели плотности интервалов (абсолютные или относительные). В этом случае высоты прямоугольников гистограммы будут соответствовать величине плотности распределения.
Рисунок 3 – Гистограмма
При увеличении числа наблюдений из одной и той же совокупности увеличивается число групп интервального ряда, что приводит к уменьшению величины интервала. При этом ломанная линия имеет тенденцию превращения в плавную кривую, которую называют кривой распределения. Кривая распределения характеризует в обобщенном виде вариацию признака и закономерности распределения частот внутри однокачественной совокупности.
|
|
|
Кумулята или кривая накопленных частот в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат – накопленные частоты или частости (рисунок 4).
Накопленной частоты, т. е. число значений, которые попали в этот интервал и все предшествующие.
Рисунок 4 – Кумулята (кривая накопленных частот)
Следует отметить, что кривая накопленных частот не убывает ни на одном участке.
Пример построения группировки рассмотрим в примерах 1 и 2.
Пример 1
Оборот и издержки обращения тридцати торговых предприятий за отчетный период составили (тыс. руб.):
| Магазины, № п/п | Оборот | Издержки обращения |
Для выявления зависимости между размером оборота и издержками обращения произведите группировку магазинов по размеру оборота, образовав пять групп магазинов с равными интервалами. В каждой группе и в целом подсчитайте:
1) число магазинов;
2) размер оборота – всего и в среднем на один магазин;
3) издержки обращения – всего и в среднем на один магазин;
4) структуру товарооборота по группам и структуру издержек обращения;
5) уровень издержек обращения
| УИО= | Издержки обращения | ×100%. |
| Товарооборот |
6) Решение оформите в разработочной и групповой таблицах. Сделайте выводы, укажите вид группировки. Постройте гистограмму и преобразуйте её в полигон. Постройте кумуляту (кривую накопленных частот).
Решение:
Составим вариационный ряд распределения, упорядочив магазины по товарообороту от большего к меньшему.
| Магазины, № п/п | Оборот | Издержки обращения | Магазины, № п/п | Оборот | Издержки обращения |
| 7 | 341 | 160 | |||
| 11 | 456 | 242 | 19 | 1199 | 635 |
| 5 | 1326 | 623 | |||
Определим величину интервала:
|
|
|
, где
i – величина интервала;
n – число групп (в данной задаче 5 группы);
Xmax, Xmin – максимальное и минимальное значение признака (1700 и 341 соответственно).
Величина интервала составит:
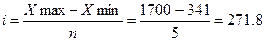
Определим границы интервалов:
| Интервал | Нижняя граница | Верхняя граница |
| 1-й | 341 + 271,8 = 612,8 | |
| 2-й | 612,8 | 612,8 + 271,8 = 884,6 |
| 3-й | 884,6 | 884,6 + 271,8 = 1156,4 |
| 4-й | 1156,4 | 1556,4 + 271,8 = 1428,2 |
| 5-й | 1428,2 | 1428,2 + 271,8 = 1700 |
Разнесем по выделенным интервалам предприятия (разработочная таблица):
| Группы предприятий по величине оборота | Номера предприятий | Число предприятий |
| 341-612,8 | 7,11 | |
| 612,8-884,6 | 21, 24, 17, 22, 25, 18 | |
| 884,6-1156,4 | 27, 12, 13, 1, 9, 14, 6, 15 | |
| 1156,4-1428,2 | 19, 5 | |
| 1428,2-1700 | 2, 30, 20, 16, 10, 29, 3, 28, 23, 4, 8, 26 |
Определим в каждой группе и в целом объем оборота – всего и в среднем на один магазин и издержки – всего и в среднем на один магазин, для чего составим группировочную таблицу:
| Группы предприятий по величине оборота | Число предприятий в группе | Суммарный товарооборот в группе | Средний товарооборот по группе | Суммарные издержки обращения по группе | Средние издержки обращения по группе | Уровень издержек обращения по группе, % |
| А | (1) | (2) | (3)=(2)/(1) | (4) | (5)=(4)/(1) | (6)=(4)/(2)*100 |
| 341-612,8 | 398,5 | 50,44 | ||||
| 612,8-884,6 | 744,5 | 345,5 | 46,41 | |||
| 884,6-1156,4 | 998,75 | 482,625 | 48,32 | |||
| 1156,4-1428,2 | 1262,5 | 49,82 | ||||
| 1428,2-1700 | 687,417 | 43,65 | ||||
| Итого | 34679/30= 1155,97 | 15843/30= 528,1 | 528,1/1155,97*100 = 45,68 |
На основании проведенных расчетов построим гистограмму и полигон.
При построении гистограммы по оси Х откладывают значения признака (границы интервалов), а по оси Y – частоты. Для соответствующего интервала строиться прямоугольник, высота которого соответствует частоте признака (рисунок 5).
Рисунок 5 – Гистограмма
Гистограмма может быть преобразована в полигон, если середины верхних граней прямоугольника соединить прямой линией (рисунок 6).
Рисунок 6 – Полигон распределения
Также построим кумуляту или кривую накопленных частот. В этом случае по оси Х откладываем интервалы признака, а по оси Y – накопленные частоты (это количество единиц совокупности, имеющие значения признака меньше указанного). Накопленные частоты рассчитаны в таблице.
|
|
|
| Группы предприятий по величине оборота | Число предприятий в группе | Накопленные частоты |
| 341-612,8 | ||
| 612,8-884,6 | 2+6=8 | |
| 884,6-1156,4 | 8+8=16 | |
| 1156,4-1428,2 | 16+2=18 | |
| 1428,2-1700 | 18+12=30 |
Кривая накопленных частот представлена на рисунке 7.
Рисунок 7 – Кривая накопленных частот
Вывод: Суммарный товарооборот в первой группе 797 тыс. руб., во второй – 4467 тыс. руб., в третьей – 7990 тыс. руб., в четвертой – 2525 тыс. руб., в пятой – 18900 тыс. руб. Средний товарооборот на один магазин в первой группе 398,5 тыс. руб., во второй – 744,5 тыс. руб., в третьей – 998,75 тыс. руб., в четвертой – 1262,5 тыс. руб., в пятой – 1575 тыс. руб.
Суммарные издержки обращения в первой группе 402 тыс. руб., во второй – 2073 тыс. руб., в третьей – 3861 тыс. руб., в четвертой – 1258 тыс. руб., в пятой – 8249 тыс. руб. Средний издержки обращения в первой группе 201 тыс. руб., во второй – 345,5 тыс. руб., в третьей – 482,625 тыс. руб., в четвертой – 629 тыс. руб., в пятой – 687,417 тыс. руб.
На основании полученных значений можно сделать вывод о прямой зависимости между размером оборота и средними издержек обращения: при росте размера оборота средние издержки обращения увеличиваются. На основании анализа уровня издержек обращения можно сделать вывод, что наиболее конкурентны предприятия пятой группы, поскольку у них уровень издержек ниже среднего.
Пример 2
По данным таблицы постройте ряды распределения домохозяйств, рассчитав число домохозяйств, входящих в те или иные группы:
а) по числу совместно проживающих человек (1,2,3,4 и более)
б) по среднему размеру доходов на душу населения в месяц (образовав 5 групп с равными интервалами)
в) по статусу занятости главы семьи.
| № п/п | Число членов в семье | Статус главы семьи по месту в занятости | Среднемесячный доход на душу, руб. |
| 1. | Самозанятость | ||
| 2. | По найму | ||
| 3. | По найму | ||
| 4. | По найму | ||
| 5. | По найму | ||
| 6. | Нет работы | ||
| 7. | Нет работы | ||
| 8. | Самозанятость | ||
| 9. | Нет работы | ||
| 10. | По найму | ||
| 11. | По найму | ||
| 12. | По найму | ||
| 13. | Самозанятость | ||
| 14. | По найму | ||
| 15. | По найму | ||
| 16. | По найму | ||
| 17. | По найму | ||
| 18. | Нет работы | ||
| 19. | Нет работы | ||
| 20. | Самозанятость | ||
| 21. | Нет работы | ||
| 22. | По найму | ||
| 23. | По найму | ||
| 24. | По найму | ||
| 25. | По найму | ||
| 26. | По найму | ||
| 27. | Самозанятость | ||
| 28. | Нет работы | ||
| 29. | По найму | ||
| 30. | По найму | ||
| Итого | - | - |
Решение:
Построим ряды распределения домохозяйств, рассчитав число домохозяйств, входящих в те или иные группы:
Общее число семей, имеющих разный статус глав семей по месту в занятости, представлено в таблице. В этом случае группировка строиться по качественному признаку. Число групп совпадает с числом признаков: самозанятость, по найму, нет работы.
| Статус главы семьи по месту в занятости | Число семейств |
| По найму | |
| Нет работы | |
| Самозанятость | |
| Итого |
Общее число глав семей, имеющих разный статус по месту в занятости (са Общее число семей, имеющих разный статус глав семей по месту в занятости, представлено в таблице. В этом случае группировка строиться по качественному признаку. Число групп совпадает с числом признаков: самозанятость, по найму, нет работы.
Группировка по числу совместно проживающих человек (1,2,3,4 и более), представлено в таблице. В этом случае группировка строиться по количественному дискретному признаку.
| Число членов в семье | Число семейств | Доля, % |
| 4 и более | ||
| Итого | 100,0 |
Таким образом, 33% всех обследованных семей состоят из трех человек. 13% семей состоят из 4 и более человек. Доли семей, состоящих из 1 человека – 17%, из 2 человек – 37%.
Построим группировку по среднему размеру доходов на душу населения в месяц (образовав 5 групп с равными интервалами);
На начальном этапе проранжируем ряд от меньшего к большему:
| Номер домохозяйства | Среднемесячный доход на душу, руб. | Номер домохозяйства | Среднемесячный доход на душу, руб. |
Определим величину интервала по формуле:
, где
i – величина интервала;
n – число групп (в данной задаче 5 группы);
Xmax, Xmin – максимальное и минимальное значение признака.
Величина интервала составит:
Разнесем по выделенным интервалам домашние хозяйства:
| Группы домашних хозяйств по величине среднемесячного дохода на душу | Число домашних хозяйств | Доля, % |
| 2140-4800 | ||
| 4800-7460 | ||
| 7460-10120 | ||
| 10120-12780 | ||
| 12780-15440 | ||
| Итого |
Это и будет интервальный ряд распределения.
Рисунок 8 – Гистограмма распределения
Таким образом, в 50% всех обследуемых домашних хозяйствах среднедушевой доход составляет от 4800 рублей до 7460 рублей на человека. Доход от 2140 до 4800 рублей на человека наблюдается в 16% всех семей. Доход от 7460 до 10120 рублей на человека наблюдается в 20% всех обследованных семей. Доля семей, где среднедушевой доход составляет от 10120 до 12780, а также от 12780 до 15440 рублей, равна 7%.
Вопросы для самопроверки
|
|
|
