 |
Суточный ход метеоэлементов
|
|
|
|
Суточный ход метеоэлементов вызван колебаниями интенсивности лучистой энергии, поступающей на поверхность Земли. Температура деятельного слоя почвы изменяется соответственно притоку солнечной радиации. Благодаря турбулентному теплообмену поверхности с воздухом и молекулярному с нижележащими слоями почвы, тепловая волна распространяется от поверхности вверх и вниз.
Изменение в течение суток температуры воздуха на высоте  и почвы на глубине
и почвы на глубине  при предположении о постоянстве по вертикали коэффициентов температуропроводности воздуха (его чаще называют коэффициентом турбулентности для тепла)
при предположении о постоянстве по вертикали коэффициентов температуропроводности воздуха (его чаще называют коэффициентом турбулентности для тепла)  и почвы
и почвы  и аппроксимации суточного хода радиационного баланса одной гармоникой
и аппроксимации суточного хода радиационного баланса одной гармоникой  , можно рассчитать по формуле (см. /2/ (7.4)):
, можно рассчитать по формуле (см. /2/ (7.4)):
 , (2.11)
, (2.11)
где i =1 – для почвы и i =2 – для воздуха;  и
и  - среднесуточные значения радиационного баланса и температуры;
- среднесуточные значения радиационного баланса и температуры;  - амплитуда радиационного баланса;
- амплитуда радиационного баланса;  - угловая скорость вращения Земли (см. прил. 3 /2/);
- угловая скорость вращения Земли (см. прил. 3 /2/);  - удельная теплоемкость воздуха (прил. 3 /2/);
- удельная теплоемкость воздуха (прил. 3 /2/);  - скрытая теплота испарения воды (прил. 3 /2/);
- скрытая теплота испарения воды (прил. 3 /2/);  - относительная влажность воздуха вблизи поверхности почвы в долях единицы;
- относительная влажность воздуха вблизи поверхности почвы в долях единицы; 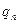 - насыщенное значение массовой доли водяного пара, для определения которой можно использовать таблицу прил. 8 /2/;
- насыщенное значение массовой доли водяного пара, для определения которой можно использовать таблицу прил. 8 /2/;  - плотность воздуха;
- плотность воздуха;  - объемная теплоемкость почвы (см. прил. 24, /2/); t – время, отсчитываемое от полудня.
- объемная теплоемкость почвы (см. прил. 24, /2/); t – время, отсчитываемое от полудня.
Для анализа результатов решения задачи и сравнения суточного хода температуры с заданной функцией суточного хода радиационного баланса на поверхности почвы удобно в формуле 2.11 перейти от функции sin к функции cos, используя известное соотношение:
 . В этом случае формула 2.11 преобразуется к виду:
. В этом случае формула 2.11 преобразуется к виду:

Используя (2.11) нетрудно получить выражение, позволяющее определить суточный ход турбулентного потока тепла на поверхности  .
.
|
|
|
Поскольку  , то при постоянном по высоте коэффициенте
, то при постоянном по высоте коэффициенте  после дифференцирования (2.11) получим:
после дифференцирования (2.11) получим:
 . (2.12)
. (2.12)
Задача. Рассчитать температуру на высоте 2 м, если ее среднесуточное значение равно  , и турбулентный поток на поверхности в 17 ч., амплитуда радиационного баланса составляет
, и турбулентный поток на поверхности в 17 ч., амплитуда радиационного баланса составляет  , почва слабо увлажнена, относительная влажность воздуха вблизи поверхности 50%, а коэффициент температуропроводности воздуха равен
, почва слабо увлажнена, относительная влажность воздуха вблизи поверхности 50%, а коэффициент температуропроводности воздуха равен  . Среднесуточное значение турбулентного потока тепла
. Среднесуточное значение турбулентного потока тепла 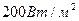 .
.
Решение.
1. По табл. прил. 8 /2/ определяем:
 , 1‰=1 г/кг
, 1‰=1 г/кг
- По табл. прил. 24 /2/ находим для слабоувлажненной почвы:
 ,
,  .
. - Вычислим общий множитель в формулах (2.11) и (2.12), обозначив его символом В:
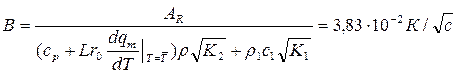 .
.
- Вычислим амплитуду (максимальное отклонение температуры от ее среднесуточного значения) колебаний температуры поверхности. Формула для нее следует из (2.11) при значении
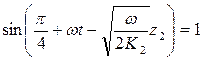 ,
,
 .
.
- Вычисляем
 ,
,
 .
.
- Вычисляем отклонение температуры от среднесуточного значения:
 ,
,
 ,
,

- Вычисляем отклонение турбулентного потока тепла у поверхности от его среднесуточного значения:

- Определяем искомые величины:
 ,
,
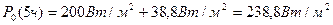 .
.
Ответ:  ,
,  .
.
Трансформация полей температуры и влажности
При переходе воздушной массы с одной подстилающей поверхности «старой» на другую «новую», имеющую существенно отличные температуру и влажность, в результате турбулентного обмена в ней изменяются профили этих свойств. Трансформированная под влиянием «новой» поверхности температура или влажность на расстоянии x от границы раздела на высоте может быть вычислена по формуле:
 , (2.13)
, (2.13)
где  - распределение свойства
- распределение свойства  или
или  над «старой» подстилающей поверхностью (см. /2/, §7.5);
над «старой» подстилающей поверхностью (см. /2/, §7.5);  - параметр стратификации, равный 0,1 – при неустойчивой стратификации; 0,14 – при безразличном равновесии; 0,25 – при инверсиях.
- параметр стратификации, равный 0,1 – при неустойчивой стратификации; 0,14 – при безразличном равновесии; 0,25 – при инверсиях.
Функция  определяется по графику приложения 25 /2/ по значению
определяется по графику приложения 25 /2/ по значению  :
:
|
|
|
 ,
,
где  - высота, на которой определяются
- высота, на которой определяются  и
и  .
.
С трансформацией связано такое важное явление, как адвективный туман. Рассчитав по формуле (2.13) значения массовой доли водяного пара q и температуры, по которой, используя таблицу прил. 8 /2/, легко определить насыщающее значение  , можно вычислить относительную влажность
, можно вычислить относительную влажность 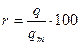 . И таким образом, судить о возможности образования тумана.
. И таким образом, судить о возможности образования тумана.
Дифференцируя (2.13) по z и полагая затем, что z=0, получим выражение для турбулентного потока тепла или водяного пара с «новой» поверхности, как функцию расстояния от границы раздела:
 , (2.14)
, (2.14)
где  - плотность воздуха,
- плотность воздуха, 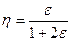 ,
,  - интеграл Эйлера 2-го рода (гамма-функция), который вычисляется с помощью табл. прил. 22 /2/.
- интеграл Эйлера 2-го рода (гамма-функция), который вычисляется с помощью табл. прил. 22 /2/.
В указанной таблице приводятся значения Г( ) для
) для  . Поэтому, в случае, если
. Поэтому, в случае, если  , следует воспользоваться формулой:
, следует воспользоваться формулой:
 .
.
Задача 1. Как изменится относительная влажность на высоте 10 м в воздушной массе после того, как последняя прошла 15 км над морем, если в момент, когда она подошла к поверхности моря, распределение температуры и влажности в ней описывалось следующими уравнениями:
 ,
,
 .
.
Температура поверхности моря 15°С. Коэффициент турбулентности и скорость ветра на высоте 1 м равны соответственно 0,2 м2/с и 10 м/с.
Решение.
1. Рассчитываем относительную влажность на высоте 10 м в воздушной массе над сушей. Для этого вычисляем:

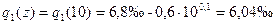
По  в табл. прил. 8 /2/ находим
в табл. прил. 8 /2/ находим  и вычисляем относительную влажность:
и вычисляем относительную влажность:

- Вычисляем температуру и влажность на высоте 10м над «новой» поверхностью (над морем) на расстоянии 15 км от берега. Для этого вычисляем:
а) 

б) используя график приложения 25 /2/, по  и
и  находим
находим

в) вычисляем температуру по формуле (2.13):

г) находим значение массовой доли водяного пара «новой» поверхности  . Поскольку таковой является поверхность воды, то величина фактической доли водяного пара
. Поскольку таковой является поверхность воды, то величина фактической доли водяного пара  равна ее насыщающему значению
равна ее насыщающему значению  и может быть определена по табл. прил. 8 /2/ по температуре поверхности моря:
и может быть определена по табл. прил. 8 /2/ по температуре поверхности моря:

д) по формуле (2.13) вычисляем фактическое значение  на высоте 10 м над уровнем моря:
на высоте 10 м над уровнем моря:

е) по температуре  находим в табл. прил. 8 /2/ максимальное значение:
находим в табл. прил. 8 /2/ максимальное значение:

3. Вычисляем относительную влажность на высоте 10м над морем на расстоянии 15км от берега

4. Находим изменение относительной влажности
|
|
|
 .
.
Таким образом, с переходом на поверхность моря относительная влажность воздуха на высоте 10 м увеличилась на расстоянии 15км от берега на 5%.
Задача 2. Определить турбулентный поток водяного пара (скорость испарения) с поверхности моря с температурой 15° на расстоянии 10км от берега, если на нее поступает воздух с суши, где он имеет у поверхности температуру 7°, а относительная влажность 70%. Коэффициент турбулентности и скорость ветра на высоте 1м равны соответственно 0,5 м2/с и 5 м/с. Термическая стратификация устойчивая.
Решение.
1. Определяем массовую долю водяного пара вблизи «старой» и «новой» подстилающих поверхностей:
а) в табл. прил. 8 /2/ по температуре суши 7° находим насыщающее значение  , умножив которое на относительную влажность, получим фактическое:
, умножив которое на относительную влажность, получим фактическое:

2. Определим  :
:
а) Вычислим  , имея в виду, что при устойчивой стратификации
, имея в виду, что при устойчивой стратификации  :
:

б) по табл. прил. 22 /2/ найдем 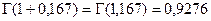 и
и  .
.
3. По формуле (2.14), подставляя вместо  q, вычислим скорость испарения:
q, вычислим скорость испарения:
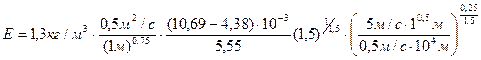
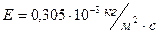
Контрольная работа №2.
Задача 1.
аходим в табл. я:
кое значение
ической доли водяного пара шной массе над сушей. еделение температуры и влажности вней опиВариант 1.
Рассчитать напряжение турбулентного трения, турбулентные потоки тепла и влаги в приземном слое, а также значение коэффициента турбулентности на высоте 10 м, используя следующие данные градиентных измерений:
| z | м | 1,0 | 5,0 |
| u | м/с | 4,5 | 5,8 |
| t | ˚С | 18,0 | 17,5 |
| q | ‰ | 8,2 | 7,6 |
При расчетах принять  ;
;  ;
;  .
.
Определить скорость испарения в приземном слое, а также значения скорости ветра, температуры, массовой доли водяного пара, а также значение коэффициента турбулентности на высоте 10 м, используя следующие данные градиентных измерений:
| z | м | 1,0 | 4,0 |
| u | м/с | 6,5 | 7,5 |
| t | ˚C | 21,4 | |
| q | ‰ | 10,4 |
Вариант 3.
Определить шероховатость подстилающей поверхности, динамическую скорость и турбулентный поток влаги в приземном слое, используя следующие данные градиентных наблюдений:
| z | м | 0,5 | 1,0 | 2,0 | 4,0 | 8,0 |
| u | м/с | 3,5 | 4,2 | 4,5 | 5,4 | 5,9 |
| q | ‰ | 14,1 | 13,6 | 13,1 | 12,4 | 11,8 |
Плотность воздуха принять равной 1,3 кг/м3. Применить графический метод решения. График выполнить на миллиметровке.
|
|
|
Вариант 4.
Определить шероховатость подстилающей поверхности, коэффициент турбулентности на высоте 10 м, напряжение турбулентного трения и скорость испарения в приземном слое, используя данные градиентных наблюдений:
| z | м | 0,5 | 1,0 | 2,0 | 5,0 | 10,0 |
| u | м/с | 2,2 | 2,6 | 2,8 | 3,3 | 3,6 |
| q | ‰ | 18,0 | 17,2 | 16,6 | 15,7 | 15,0 |
Плотность воздуха принять равной 1,3кг/м3. Применить графический способ решения. График выполнить на миллиметровке.
Задача 2.
Вариант 1.
Определить скорость ветра и отклонение его направления от направления изобар в пограничном слое атмосферы на высотах 50 м, 200 м, 500 м и 800 м, если геострофический ветер не меняется по высоте и равен 8 м/с. Рассчитать силу турбулентного трения на этих же высотах, а также высоту пограничного слоя (уровень совпадения реального и геострофического ветра по направлению).
Расчеты произвести для широты 60˚ при неустойчивой стратификации 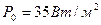 . Плотность принять равной 1,3 кг/м3, среднее значение температуры
. Плотность принять равной 1,3 кг/м3, среднее значение температуры  . На основании расчетов построить годограф скорости.
. На основании расчетов построить годограф скорости.
Вариант 2.
На широте 55˚ скорость геострофического ветра 10 м/с, горизонтальный градиент давления в пределах пограничного слоя не меняется с высотой. Рассчитать значение среднего по высоте пограничного слоя коэффициента турбулентности и высоту пограничного слоя для неустойчивой стратификации  (использовать условие совпадения реального ветра с геострофическим по направлению).
(использовать условие совпадения реального ветра с геострофическим по направлению).
Для высот 100 м, 300 м, 600 м и 1000 м определить:
а) горизонтальные составляющие скорости ветра, модуль и направление ветра по отношению к направлению геострофического ветра;
б) горизонтальные составляющие силы Кориолиса и силы трения.
На основании расчетов построить годограф скорости. При расчетах принять  ,
,  .
.
Вариант 3.
Скорость геострофического ветра на широте 65˚ в пределах пограничного слоя атмосферы не меняется с высотой и равна 11 м/с. Средний вертикальный градиент температуры в пограничном слое равен  . Определить величину и направление
. Определить величину и направление
(по отношению к направлению геострофического ветра) скорости ветра и силы турбулентного трения на высотах 150 м, 400 м и 800 м, высоту пограничного слоя (из условия  ), а также среднее по высоте значение коэффициента турбулентности. При расчетах принять
), а также среднее по высоте значение коэффициента турбулентности. При расчетах принять  ,
,  .
.
Вариант 4.
Горизонтальный градиент давления на широте 50˚ в пределах пограничного слоя атмосферы не меняется с высотой и составляет 2гПа/100 км. При этом давление убывает с юга на север. Считая, коэффициент турбулентности постоянным по высоте, определить величину и направление скорости ветра и силы турбулентного трения на высотах 100, 500 и 1000 м. Рассчитать высоту пограничного слоя и значение среднего по высоте коэффициента турбулентности. Расчеты произвести для условий стратификации, характеризуемых значением среднего вертикального градиента температуры  . Принять
. Принять  ,
, 
|
|
|
Задача 3.
1. По данным табл. 1, соответствующим Вашему варианту, рассчитать и построить:
а) суточный ход температуры воздуха на двух высотах;
б) суточный ход турбулентного потока тепла у поверхности.
2. Определить:
а) время наступления максимального значения температуры и турбулентного потока тепла;
б) высоту теплового пограничного слоя, приняв, что на этой высоте n=20.
| № варианта | 
| 
| 
| Состояние почвы | 
| 
| 
|
| Слабо увлажнена | |||||||
| Хорошо увлажнена | |||||||
| Сухая | |||||||
| Сильно увлажнена |
3. Проанализировать полученные результаты.
Расчеты суточного хода выполнять для t=2, 4, 6, 8…24 ч. При построении графиков откладывать астрономическое время.
Задача 4.
Вариант 1.
Будет ли образовываться туман в воздухе на уровне 6 м после того, как он пройдет 20 км над морем, если распределение температуры и влажности его над описывалось соответственно: 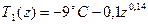 ;
;  , а температура поверхности моря -2˚С. Коэффициент турбулентности и скорость ветра на высоте 1 м соответственно равны 0,1 м2/с и 10 м/с.
, а температура поверхности моря -2˚С. Коэффициент турбулентности и скорость ветра на высоте 1 м соответственно равны 0,1 м2/с и 10 м/с.
Определить толщину трансформированного слоя на этом расстоянии, приняв за его верхнюю границу уровень, на котором
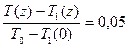
Вариант 2.
Определить турбулентный поток тепла на расстоянии 5 км от берега над водной поверхностью с температурой 15˚С, если температура воздушной массы над сушей 5˚С, коэффициент турбулентности и скорость ветра на высоте 1 м равны соответственно 0,5м2/с и 5 м/с. Термическая стратификация неустойчивая. Ветер дует с суши на море. Как изменится эта величина при устойчивой стратификации?
Вариант 3.
Как изменится относительная влажность на высоте 2 м в воздушной массе после того, как она пройдет 15 км над морем, если над сушей в ней имело место следующее распределение температуры и влажности:
 ;
; 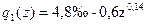 .
.
Температура поверхности моря 20˚С,  ,
,  .
.
Что такое внутренний пограничный слой? От чего зависит его толщина? Оценить ее по условиям задачи, приняв, что на его верхней границе

Вариант 4.
Рассчитать скорость испарения с водоема, температура поверхности которого 10˚С, на расстоянии 10 км от берега, если на него поступает воздух с суши, имеющий температуру 0˚С. Коэффициент турбулентности и скорость ветра на высоте 1 м равны соответственно 0,8 м2/с и 8 м/с. Термическая стратификация равновесная. Влажность воздуха над сушей была 60%. Как изменится и чему будет равна скорость испарения на расстоянии 20 км от берега? Объясните причину этого изменения.
|
|
|


