 |
Системы линейных уравнений и неравенств с двумя неизвестными
|
|
|
|
Кафедра математики
Методические указанияи задания к выполнению
расчетно-графической работы по теме:
«Линейная алгебра и аналитическая геометрия»
для студентов всех специальностей и всех направлений подготовки бакалавров
очной формы обучения
Брянск 2015
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Брянский государственный инженерно-технологический университет»
Кафедра математики
УТВЕРЖДЕНЫ
научно-методическим
советом университета
Протокол № ____
oт “____”___________2015 г.
Методические указанияи задания к выполнению
расчетно-графической работы по теме:
«Линейная алгебра и аналитическая геометрия»
для студентов всех специальностей и всех направлений подготовки бакалавров
очной формы обучения
Брянск 2015
Составители: старший преподаватель Козлова О.Н.,
доцент Охлупина О.В.
Рецензент:
профессор кафедры «Физика», д. ф.-м. н. Евтюхов К.Н.
Рекомендованы редакционно-издательской и методической комиссиями механико-технологического факультета БГИТУ.
Протокол № 1 от 10.09.2015 г.
Линейные уравнения и неравенства с двумя неизвестными
Уравнением с двумя неизвестными называется выражение вида:
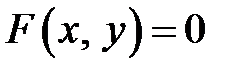(1.1).
Если из уравнения (1.1) можно выразить переменную 
, то получим уравнение вида
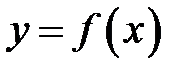(1.2).
Если уравнение (1.2) имеет вид 
или
(1.3),
то уравнение называют линейным, а графиком этой зависимости является прямая линия.
Из элементарной геометрии известно, что через две точки проходит единственная прямая. Это значит, что для построения прямой достаточно знать координаты двух точек, принадлежащих данной прямой.
|
|
|
Пример 1. Построить прямую по ее уравнению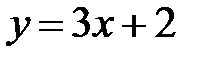 
.
Решение.
|
и определим координаты двух точек, принадлежащих этой прямой: при 
; при 
. Нанесем эти точки на координатную плоскость и проведем через них прямую (Рис.1).
|
|
|
|
|
|
|
|
|
Рис. 1.
Линейным неравенством с двумя неизвестными называют неравенство вида
, где 
и 
- действительные числа.
Точки плоскости , удовлетворяющие уравнению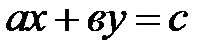 
(1.4) расположены на прямой, делящей всю координатную плоскость на две полуплоскости 
и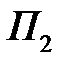 
. В одной из этих полуплоскостей выполняется неравенство 
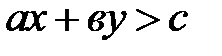, в другой - 
.
Пример 2. Решить неравенство 
и изобразить область решения на плоскости .
Решение. Построим прямую 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.
Определим координаты двух точек, принадлежащих прямой: при 
; при 
. Нанесем точки на координатную плоскость и построим прямую, проходящую через эти точки. Для определения области решения неравенства, возьмем произвольную точку плоскости, не лежащую на прямой, например 
и подставим ее координаты в заданное неравенство: 
, т.е. неравенство не выполняется, следовательно, областью решения заданного неравенства служит полуплоскость, не содержащая точку 
(Рис.2).
Системы линейных уравнений и неравенств с двумя неизвестными
Системой двух линейных уравнений с двумя неизвестными называют совокупность двух уравнений вида:
(2.1).
Решением системы (2.1) называют пару чисел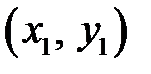 
, удовлетворяющих каждому уравнению системы т.е.:
.
Каждое уравнение системы определяет прямую на плоскости, следовательно, решение системы есть точка пересечения этих прямых. Найдем координаты этой точки. Выразим из первого уравнения системы неизвестное 
и подставим его во второе уравнение: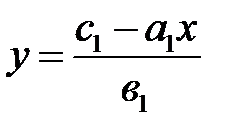 
; 
; 
.
.
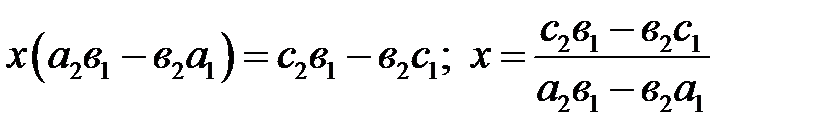Подставим значение 
в выражение , получим: 
.
|
|
|
Введем обозначение: 
. Величину 
будем называть определителем второго порядка системы (2.1). Тогда 
, 
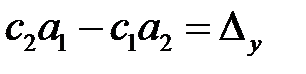будем называть вспомогательными определителями системы. Запишем определители в виде таблиц, состоящих из двух строк и двух столбцов:
.
Как видно, определитель системы составлен из коэффициентов при неизвестных первого и второго уравнений. Определители 
и 
получены из определителя 
, путем замены первого и второго столбцов, соответственно, столбцом свободных членов системы, что и оправдывает обозначения и .
Очевидно, что решение системы (2.1) можно записать в виде: 
.
Пример 3. Решить систему:
.
Решение. Вычислим определитель :
.
Определитель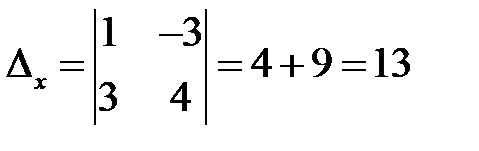 
.
Определитель 
. Тогда: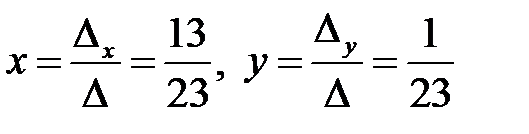 
.
Ответ: 
.
Система линейных неравенств с двумя неизвестными имеет вид:
(2.2)
где 
- коэффициенты системы; 
- свободные члены или правые части неравенств, - действительные числа. Так как решением каждого неравенства системы является полуплоскость, то решением системы служит многоугольник, координаты точек которого удовлетворяют каждому неравенству системы. Можно показать, что этот многоугольник выпуклый.
Пример 4. Решить систему неравенств. Многоугольник решений изобразить на чертеже.
Решение. Найдем решение каждого неравенства системы. Заменим в каждом неравенстве знак неравенства на знак равно.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
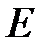
Рис. 3.
Решением служит многоугольник 
.
Матрицы и определители
Матрицей порядка 
называют таблицу чисел, состоящую из 
- строк и 
- столбцов.
Числа, входящие в состав матрицы, называют элементами матрицы. Для обозначения матрицы используют заглавные буквы латинского алфавита 
. Элементы матрицы 
обозначают 
, где 
и 
называют индексом элемента . Первый индекс определяет номер строки, индекс - определяет номер столбца матрицы . Если число строк матрицы равно числу столбцов, то матрицу называют квадратной. Если матрица состоит из одной строки, ее называют матрица-строка, если матрица состоит из одного столбца, то ее называют матрицей-столбцом. Если у квадратной матрицы элементы 
при 
, то матрицу называют диагональной. Если у диагональной матрицы все элементы 
, то матрицу называют единичной матрицей. Единичную матрицу обозначают буквой 
. Например:
|
|
|
.
Матрицы одинакового порядка можно складывать и вычитать.
Суммой двух матриц и 
одинакового порядка называют матрицу 
того же порядка, элементы которой вычисляют по правилу
(3.1).
Аналогично определяют разность матриц.
Пример 5. Найти сумму и разность матриц и .
.
.
.
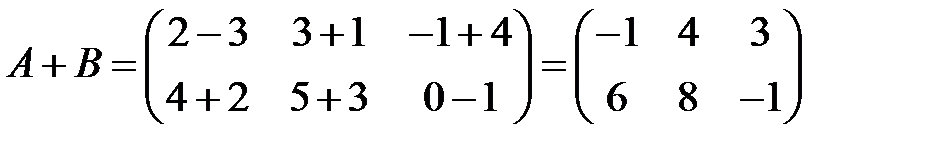Произведением матрицы 
на число 
называют матрицу 
, элементы которой вычисляют по формуле
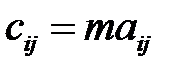(3.2).
Пример 6. Матрицу 
умножить на 
.
Решение. 
.
Произведением двух матриц порядка 
и 
порядка 
называют матрицу 
порядка 
, элементы которой определяют по формуле:
(3.3).
Замечание 1. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Пример 7. Найти произведение матриц и , если
.
Решение.
Квадратная матрица порядка 
называется обратной матрицей матрицы порядка 
, если 
.
Замечание 2. Произведение матриц не обладает свойством коммутативности, то есть в общем случае:
.
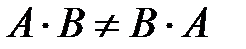Если 
, то матрицы называют коммутативными.
Замечание 3. Для обратных матриц справедливо равенство 
.
Обратную матрицу принято обозначать 
.
|
|
|
