Суть моды и формула ее использования.

Характеристиками структуры совокупности являются следующие структурные средние: Мода (Mo) — величина признака, наиболее часто встречающаяся в совокупности, т.е. имеющая наибольшую численность в ряду распределения. а) В дискретном ряду распределения мода определяется визуально. б) В интервальном ряду распределения визуально можно определить только интервал, в котором заключена мода, который называется модальным интервалом. Мода будет равна: 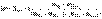, где Х_Mo – нижнее значение модального интервала; m_Mo – число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении); m_Mo-1 – то же для интервала, предшествующего модальному; m_Mo+1 – то же для интервала, следующего за модальным; h – величина интервала изменения признака в группах. Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой.

Виды относительных величин.

Абсолютные величины сами по себе не дают достаточной характеристики оценки явления. Поэтому в статистике наряду с абсолютными величинами используются относительные, которые представляют собой показатели, характеризующие количественные соотношения, присущие конкретным экономическим явлениям (удельный вес городского и сельского населения в общей численности). Отличительной особенностью относительных величин является то, что они обычно в отвлеченной форме выражают соотношение либо индивидуальных, либо суммарных абсолютных величин. К относительным величинам в статистике относят некоторые именованные числа. Подобного рода относительные величины показывают, сколько единиц одной совокупности приходится на единицу другой. При вычислении относительных величин производится сравнение одного или нескольких показателей с базой или основанием (базисной величиной). В зависимости оттого, что именно сравнивать, какие соотношения надо получить, используют в статистике несколько видов относительных величин: 1. относительные величины выполнения планового задания - такие величины, которые выражают соотношения между фактическими показателями и теми, которые планировались. 2. относительные величины структуры. Величина структуры очень важна в статистике и представляет собой соотношение части и целого. При исчислении величины структуры в качестве базы берется общий итог совокупности (общие размеры), а в качестве сравнительных величин берутся значения показателей отдельных групп или отдельных частей. Поэтому в статистике обычно называют отношение части к целому либо долей, либо удельным весом. Относительные величины структуры позволяют выяснять не только структуру, изучаемой совокупности, но и структурные сдвиги, т.е. изменение ее состава, строения, тенденцию, направление, которые произошли за определенный период времени. 3. Относительные величины координации – соотношение частей целого между собой. При расчете одну из составных частей этой совокупности принимают за базу сравнения и находят отношение к ней всех других частей. С их помощью определяют, сколько единиц данной части совокупности приходятся на другую ее часть, принятую за базу сравнения. 4. Относительные величины динамики выражают степень изменения явления во времени, т.е. они измеряют скорость (темп) развития. Относительная величина динамики есть отношение значения (уровня) показателя за данный период (месяц, квартал, год) к его уровню за предыдущее время. 5. Относительные величины сравнения представляют собой отношение одноименных величин, относящихся к разным объектам (численность населения в г. Твери и в г. Торжке). 6. Относительные величины интенсивности – показатели, характеризующие распространение, развитие какого-либо явления в определенной среде. Они измеряют степень или интенсивность распространения показателей или явлений. Чаще всего они представляют собой соотношение разноименных, но связанных явлений, где в числители – вели

Понятие средней величины.

Средняя величина представляет собой обобщенную количественную характеристику признака статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины отражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Различают следующие виды средней, каждая из которых может быть простой и взвешенной: Средняя арифметическая; Средняя гармоническая; Средняя геометрическая; Средняя квадратическая, кубическая и т.д.. Структурные средние: мода и медиана. Средняя арифметическая простая (не взвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Средняя арифметическая взвешенная. При расчете средних величин отдельные значения признака могут повторяться, встречаться по нескольку раз. В данном случае расчет проводится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными. Средняя гармоническая — это величина, обратная средней арифметической из обратных значений признака. Различают среднюю гармоническую простую и взвешенную. Средняя гармоническая взвешенная применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение. Мода — Это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. Медиана лежит в середине ранжированного ряда и делит его пополам.

,