Основные показатели анализа динамики.

А) Для характеристики динамики рядов используют абсолютный прирост, представляющий собой разность уровней ряда динамики. Абсолютный прирост показателей либо увеличивает прирост показателей, либо увеличение уровня ряда за определенный период времени. Чтобы определить размер увеличения показателя за весь период времени, охватываемый ряд динамики, находят общий абсолютный прирост, который равен сумме последовательно вычисляемых абсолютных приростов, и вместе с тем, он равен разности между конечным и начальным уровнем. Цепной абсолютный прирост - . Базисный абсолютный прирост - . Цепной абсолютный прирост характеризует последовательное изменение уровней ряда, а базисный абсолютный прирост - изменение нарастающим итогом. Абсолютный прирост показывает, на сколько абсолютных единиц изменился данный уровень по сравнению:
а) с предыдущим уровнем при цепном способе; б) с начальным уровнем при базисном способе. Между цепным и базисным абсолютным приростом существует взаимосвязь - сумма цепных дает соответствующий базисный абсолютный прирост.

Б) Поскольку абсолютный прирост показателей, на сколько единиц в абсолютном выражении, уровень последующего периода больше или меньше уровня предшествующего, то мы не можем получить ответ на вопрос во сколько раз уровень одного периода больше или меньше уровня другого. Поэтому в статистике используют показатель темпа роста, т.е. отношение уровня данного периода к уровню периода ему предшествующего. Иногда используют не предшествующее значение, а другое, принятое за базу. Обычно темпы роста выражаются в виде процентов, либо в виде простых отношений и коэффициентов. Темпы, выраженные в виде простых отношений, называют коэффициентом роста.

Темп роста (Тр) - это соотношение последующего уровня ряда к предыдущему (цепные темпы роста) или постоянному, принятому за базу сравнения (базисные темпы роста). цепной , базисный . Между цепными и базисными темпами роста существует взаимосвязь - произведение цепных темпов роста дает соответствующий базисный темп роста.

В) Темп прироста используется для выражения величины абсолютного прироста уровней ряда динамики в относительных величинах: Он показывает, на какую величину — долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня. Темп прироста показывает, на сколько процентов изменяется данный уровень по сравнению:
а) с предыдущим уровнем ряда при цепном способе, б) с базисным, начальным уровнем ряда при базисном способе. Базисные темпы прироста: . Цепные темпы прироста: . Между цепными и базисными темпами прироста существует взаимосвязь - произведение цепных темпов прироста дает соответствующий базисный темп прироста.

 

времени, в течение которых уровень не изменялся.

 

36.Средние показатели динамики.

Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим в среднем за единицу времени. Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем.

 

 

В качестве основы и критерия правильности исчисления среднего темпа роста можно использовать в роли определяющего показателя произведение цепных темпов роста, которое равно темпу роста за весь рассматриваемый период.

 

 

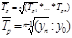Средний темп прироста (или снижения), выраженный в процентах, показывает, на сколько процентов увеличивался (или снижался) уровень по сравнению с предыдущим в среднем за единицу времени. Средний темп прироста характеризует среднюю интенсивность роста.

 

Сведение рядов динамики.

Важнейшим условием правильного построения ряда динамики является сопоставимость всех входящих в него уровней.

Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета и др.

Сопоставимость по территории предполагает одни и те же границы территории. Вопрос о том, является ли это требование непременным условием сопоставимости уровней динамического ряда, может решаться по-разному, в зависимости от целей исследования. Так, при характеристике роста экономической мощи страны следует использовать данные в имеющихся границах территории, а при изучении темпов экономического развития — данные по территории в одних и тех же границах. Объясняется это тем, что изменение границ влияет на численность населения, объем продукции.

Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов. При этом нужно иметь в виду, что сопоставляемые показатели динамического ряда должны быть однородны по экономическому содержанию и границам объекта, который они характеризуют (однородность может быть обеспечена одинаковой полнотой охвата разных частей явления).

Сопоставимость по времени регистрации для интервальных рядов обеспечивается равенством периодов времени, за которые приводятся данные. Нельзя, например, при изучении ритмичности работы предприятия сравнивать данные об удельном весе продукции по определенным декадам, т.к. число рабочих дней отдельных декад может оказаться существенно различным, что приводит к различиям в объеме выпуска продукции. Это относится и к рядам внутригодовой динамики с месячными, квартальными уровнями.

Рассмотренные примеры показывают, что часто приходится иметь дело с такими несопоставимыми данными, которые могут быть приведены к сопоставимому виду дополнительными расчетами. В ряде случаев несопоставимость может быть устранена путем обработки рядов динамики приемом, который носит название смыкание ряда динамики. Этот прием позволяет преодолеть несопоставимость данных, возникающую вследствие изменения во времени круга охватываемых объектов или методологии расчета показателей, и получить единый сравнимый ряд за весь период времени. Если, например, имеется два ряда показателей, характеризующих динамику одного и того же явления в новых и старых границах по одному и тому же кругу объектов, то такие динамические ряды можно сомкнуть.

мыкание рядов дает возможность устранить несопоставимость уровней и получить представление о динамике за весь период. Однако при этом следует иметь в виду, что результаты, полученные путем смыкания рядов, являются приближенными, т.е. содержат некоторую погрешность. Таким образом, прежде чем анализировать динамические ряды, следует убедиться в сопоставимости их уровней и, если сопоставимость отсутствует, добиться ее дополнительными расчетами, когда это возможно.

 

Коэфициент ускорения.

Если скорость за промежуток времени изменяется, то имеет смысл сравнивать одноимённые характеристики скорости или ускорения. На базе абсолютных приростов оценивается абсолютное и относительное ускорение.

Абсолютное – разница между абсолютными приростами за ровные интервалы времени.

Если абсолютное ускорение больше 0, то имеется, абсолютное ускорение, если меньше-замедление.

Вычисление темпов ускорения или замедления абсолютной скорости рассчитывают как отношение абсолютных приростов.

Сравнение темпов роста или темпов прироста в рядах динамики за одинаковые промежутки времени позволяет получить коэффициент ускорения или замедления.

К уск= Tp i/Tp i-t К уск= Tp>/ Tp<

 

Коэфициенты опережения.

Коефициент опережения показывает во сколько раз средний темп прироста одного показателя больше чем средний темп прироста другого показателя. При этом данные должны относиться к одному периоду времени. К опер= ср. Т пр. А/ ср. Т пр. Б

Коэффициенты опережения по темпам роста – это отношение темпов роста (цепных или базисных) одного ряда к соответствующим по времени темпам роста (также цепным или базисным) другого ряда. Аналогично находятся и коэффициенты опережения по темпам прироста. Коэффициент опережения должен быть больше единицы.

коефіцієнт еластичності - по-казник, що характеризує міру чутливості економічної величини по відношенню до факторів іншої величини, від яких вона за-лежить. Напр., якою мірою зміниться по-пит на товар чи послугу від зміни основно-го фактора, що впливає на попит (ціни то-вару, послуги та ін.).

Для темпов прироста рассчитывают также эмпирические коефициенты эластичности - изучают для взаимосвязанных показателей Х и У Ч= Тпр.У/ Тпр.Х Коеф. Эластичности показывает на сколько % изменится У если Х изменится на 1%

 

Статистический индекс.

Итак, статистический индекс – это относительная величина сравнения сложных совокупностей и отдельных их частей.

Следует иметь в виду, что не всякая относительная величина является индексом. Например, относительные величины структуры, интенсивности к индексам не относятся.

Индексы как сводные статистические показатели исчисляются с учетом специальных принципов и методов, которые в статистике объединяются понятием теории индексного метода.

Прежде всего, индекс – это относительный показатель, получающийся в результате сравнения двух величин, характеризующих уровень изучаемого явления для двух разных периодов.

В теории индексов тот показатель, изменение которого характеризует индекс, называется индексируемой величиной. Величина, которую сравнивают и которая стоит в числителе индексного отношения, характеризует уровень для отчетного периода: чтобы различать отчетный период принято возле символа индексируемой величины внизу ставить знак «1». Величина, с которой сравнивают и которая стоит в знаменателе индексного отношения, характеризует уровень для базисного периода (обозначается внизу символа индексируемого показателя знаком «0»).

Индекс как относительный показатель может быть выражен в виде коэффициентов (когда базовый уровень принят за 1) или в виде процентов (когда он принят за 100). Если индекс больше 1 (или 100%) уровень изучаемого явления растет, если меньше 1 (или 100%) – снижается.

Индексный метод в статистических исследованиях применяется очень широко. Можно выделить три основные сферы применения индексного метода:

- сравнительная характеристика сложных совокупностей (индексы роста и прироста, индексы выполнения плана, территориальные индексы);

- анализ динамики средних показателей: зависящих от изменения структуры совокупности;

- изучение связей и оценка доли отдельных факторов в изменении сложного явления.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: