Примеры решения тестовых заданий.

Пример 9. Объем и качество продукции трех фабрик задается таблицей

	первая	вторая	третья
Объем поставок	10 %	20 %	70 %
Процент брака	3 %	2 %	5 %

Вероятность того, выбранное наугад изделие окажется нестандартным, равна…

Решение 9. Обозначим события:

Б = {выбранное наугад изделие бракованное};

H ₁ = {изделие произвела первая фабрика};

H ₂ = {изделие произвела вторая фабрика};

H ₃ = {изделие произвела третья фабрика}.

Из условий задачи известны вероятности

P (H ₁) = 0,1;

P (H ₂) = 0,2;

P (H ₃) = 0,7, а также

P (Б | H ₁) = 0,03;

P (Б | H ₂) = 0,02;

P (Б | H ₃) = 0,05.

Поскольку других производителей у нас нет, и изделие не может быть произведено двумя фабриками одновременно, можно воспользоваться формулой полной вероятности (Определение 3.2) P (Б) = P (H ₁) P (Б | H ₁) + P (H ₂) P (Б | H ₂) + P (H ₃) P(Б | H ₃) = 0,003 + 0,004 + + 0,035 = . Задачу можно свести к классической схеме. Всего изделий n = 1000, из них 100 произведено первой фабрикой, 200 – второй и 700 – третьей. Считаем m – количество бракованных изделий. m = 3 + 4 + 35 = 42. P (Б) = .

Пример 10. В первой урне белых шаров в три раза больше, чем черных, в остальных девяти белых и черных шаров поровну. Вероятность того, что шар, извлеченный из наугад выбранной урны, окажется черным, равна...

Решение 10. Обозначим события:

Ч = {шар, извлеченный из наугад выбранной урны, оказался черным};

У₁ = {шар извлечен из первой урны};

У _n = {шар извлечен из урны с номером n, где n = 2, …, 9}.

Известны вероятности P (У₁) = P (У _n) = 0,1, а также P (Ч | У₁) = ¼; P (Ч | У _n) = ½. По формуле полной вероятности (Определение 3.2)

P (Ч) = P (У₁) P (Ч | У₁) + + 9 P (У _n) P (Ч | У _n) = .

Пример 11. В партии 4 изделия, причем все предположения о количестве нестандартных изделий равновероятны. Вероятность выбрать из партии нестандартное изделие равна…

Решение 11. Введем обозначения: Б = {выбрано нестандартное изделие}; H_n = {в партии имеется ровно n нестандартных изделий, где n = 0, …, 4}. По условию задачи («предположения о количестве нестандартных изделий равновероятны») P (H_n) = . Вычислим условные вероятности события Б.

P (Б | H ₀) = 0, поскольку если в партии нет бракованных изделий, выбрать бракованное изделие невозможно.

P (Б | H ₁) = ¼, так как есть один благоприятствующий исход из 4-х.

P (Б | H ₂) = ½, так как есть уже два благоприятствующих исхода из 4-х.

P (Б | H ₃) = ¾ и, наконец P (Б | H ₄) = 1. Воспользуемся теперь формулой полной вероятности (Определение 3.2), и получим P (Б) = .

Пример 12. В одном стакане одна игральная кость, в другом три. Наугад выбранный стакан переворачивается. Вероятность того, что на выпавших костях в сумме будет 3 очка, равна…

Решение 12. Обозначим за x сумму выпавших очков. Сформулируем две гипотезы:

H ₁ = {выбранный стакан содержит одну кость} и

H ₃ = {выбранный стакан содержит три кости}. По условию задачи («Наугад выбранный стакан») P (H ₁) = P (H ₃) = ½. Если выбранный стакан содержит одну кость, то P (x = 3 | H ₁) = . Так как граней, содержащих 3 очка всего одна из шести. Если же выбранный стакан содержит три игральные кости, то 3 очка могут выпасть только одним образом: когда на всех трех костях выпадет по 1 очку. Вероятность такого события составляет 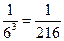. По формуле полной вероятности (Определение 3.2) получаем

P (x = 3) = P (H ₁) P (x = 3 | H ₁) + P (H ₃) P (x = 3 | H ₃) = .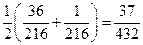

Пример 13. Среди 25 экзаменационных билетов, 7 «легких». Первый билет берет Кондратьев и уносит его с собой, следующий берет билет Иванов. Вероятность того, что Иванову достался билет с «несложными» вопросами равна …

Решение 13. Обозначим за Н = {Иванову достался «легкий» билет}. Сформулируем две гипотезы: Л = {Кондратьев унес «легкий» билет} и С = {Кондратьев унес «сложный» билет}. Вычислим P (Л) = , P (С) = 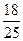. Если Кондратьев унес «легкий» билет, то в стопке билетов осталось 6 «легких» и 18 «сложных». В таком случае P (Н | Л) = . В противном случае в стопке останется 7 «легких», 17 «сложных» и P (Н | С) = . По формуле полной вероятности (Определение 3.2)

P (Н) = P (Л) P (Н | Л) + P (С) P (Н | С) = .

Кстати говоря, вероятность вытащить «легкий» билет осталась такой же, как если бы Иванов тянул билет первым.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: