Приведение сил и моментов сил

Выбор динамической модели машинного агрегата

Машинные агрегаты являются сложными многозвенными и многосвязными электромеханическими, пневмомеханическими и гидромеханическими системами. Полное описание всех аспектов динамического поведения его элементов и происходящих в нем динамических процессов не представляется возможным, как, кстати, и необходимым. В этой связи возникает необходимость абстрагирования от частных особенностей реального машинного агрегата и замены его некоторой динамической моделью.

Выбор той или иной динамической модели машинного агрегата определяется, прежде всего, характером исследуемых процессов: скоростью изменения выходных коорди­нат, частотным спектром действующих в машине активных сил и т. п. В значи­тельной степени выбор адекватной модели является эвристической процедурой, основанной, в первую очередь, на опыте конструктора. С одной стороны, ди­намическая модель должна быть достаточно простой, чтобы обеспечить прак­тическую осуществимость и эффективность решения задач динамики а, с другой стороны, достаточно сложной, чтобы гарантировать досто­верность получаемых на её основе результатов.

Во всех случаях следует стремиться к использованию наиболее простых динамических моделей, адекватных исследуемым процессам. Усложнение мо­делей, не вызванное необходимостью, приводит к введению в расчет лишних параметров машинных агрегатов, которые также определяются неточно. Свя­занные с усложнением модели дополнительные ошибки зачастую перекрывают кажущееся уточнение расчета.

Наибольшее применение в динамике машин получила одномассовая динамическая модель, т.е. расчетная схема с одним звеном (звеном приведения), координата (и её производные) которого совпадают с обобщенной координатой (и её производными) механизма в любой момент времени.

Эта расчетная схема, при всей своей простоте, отражает многие характерные особенности поведения машинных агрегатов с жесткими звеньями. Учет упругих свойств звеньев приводит к необходимости применения более сложных двухмассовых и многомассовых расчетных схем.

Для получения динамических моделей машинных агрегатов используется метод приведения сил и масс к какому-либо звену механизма.

В качестве звена приведения целесообраз­но выбрать такое, которое не изменяет направление движе­ния в пределах одного цикла работы механизма. В противные случаи приведенные силы и моменты будут достигать бесконечно больших величин. Таким звеном приведения может быть выбрано ведущее или начальное звено механизма, совершающее непрерывное вращательное или поступательное движения.

Для того, чтобы движение реального механизма или машины было эквивалентным движению динамической модели, необходимо выполнение следующих условий (условий приведения):

1. Кинетическая энергия звена приведения должна быть равна сумме кинетических энергий всех звеньев механизма или машины;

2. Работа или мощность условных сил, приложенных к звену приведения, должна быть равна сумме работ или мощностей всех реальных внешних сил и моментов сил, действующих на механизм или машину.

Таким образом, работу всех внешних сил, действующих в механизме, можно заменить работой одной приведенной силы или момента силы, а кинетическую энергию всех звеньев механизма — соответственно кинетической энергией приведенной массы или приведенного момента инерции.

Приведение сил и моментов сил

Определим значения приведенных сил и моментов сил, принимая в качестве звена приведения ведущее звено, совершающее поступательное и вращательное движения.

Для этого воспользуемся вторым условием приведения, согласно которому для сохранения эквивалентности динамической модели реальному механизму работа или мощность условных сил или моментов сил, приложенных к звену приведения, должна быть равна сумме работ или мощностей всех реальных внешних сил и моментов сил, действующих на механизм

(1)

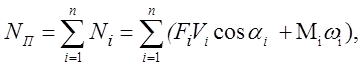
где N_п – мощность приведенной силы; N_i – мощность внешней силы; F _i – внешняя сила; V_i – скорость точки приложения внешней силы; α_i – угол между векторами внешней силы и скорости точки её приложения; M_i – момент пары сил, приложенных к звену; ω_i – угловая скорость звена; n – число подвижных звеньев.

 

Пусть звено приведения совершает поступательное движение. Тогда

N_п=F_п•V_A,

где F_п – приведенная сила; V_A – скорость т. А звена.

Подставляя это выражение в (1), получим

F_П = N_П /V_A = / V_A = (F_i V_i cos α_i / V_A + M_i ω_i). (2)

Приведенной силой называется такая условная сила, приложенная к звену приведения, работа или мощность которой равна сумме работ или мощностей всех внешних сил и моментов сил, действующих на звенья механизма.

Если звено приведения совершает вращательное движение, то

N_п=M_п•ω,

где M_п – приведенный момент сил; ω – угловая скорость

звена приведения.

Подставляя это выражение в (1), получим

M_П = N_П / ω = / ω = (F_i V_i cos α_i / ω + M_i ω_i / ω). (3)

Приведенным моментом сил называется такой условный момент, приложенный к звену приведения, работа или мощность которого равна сумме работ или мощностей всех внешних сил и моментов сил, действующих на звенья механизма.

Установим связь между приведенной силой и приведенным моментом сил.

 

Если известен приведенный момент, то из условия

N_п=F_п•V_A=М_П•ω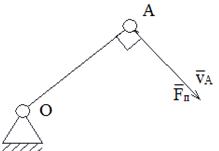

приведенная сила равна

F_П = = = ,

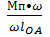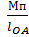так как V_A=ω•l_OA.

Если известна приведенная сила, то приведенный момент

M_П =F_П • l_OA.

Для нахождения приведенных сил можно

использовать рычаги Жуковского, так как приведенные

силы будут направлены в сторону, противоположную

направлению уравновешивающих сил.

При решении практических задач приведенные силы и моменты сил обычно разделяют на две составляющие: приведенные движущие силы и моменты сил и приведенные силы и моменты сил сопротивления.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: