 |
Средние показатели структуры
|
|
|
|
Мода (Мо) — это наиболее часто встречающееся значение признака в статистической совокупности или значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по разному.
В дискретных вариационных рядах мода – это признак, которому соответствует наибольшая частота.
В зависимости от того, равны интервалы между собой или нет, применяют тот или иной подход к определению моды. Для определения моды в интервальных вариационных рядах с равными интервалами сначала по наибольшей частоте находят модальный интервал, затем рассчитывают моду по формуле:
, (3.24)
где 
– начало модального интервала,
– длина модального интервала,
– частоты интервалов, стоящих перед модальным, модального и после модального.
Для получения более полной характеристики вариационного ряда помимо средней величины и моды рассчитываются так называемые структурные показатели. К ним относятся медиана, квартили, децили и перцентили.
Медианой (Me) является значение варианты, находящейся в центре упорядоченной по возрастанию значений признака совокупности. Медиана делит вариационный ряд на две равные части. При этом 50% единиц совокупности имеют значение меньше медианного, а 50% - больше медианного.
В дискретном ряду распределения медиана находится по номеру. Номер медианы находится по формуле:
, (3.25)
где n – число единиц в совокупности.
При четном количестве единиц в совокупности медиана получается путем расчета средней арифметической из двух рядом стоящих значений признаков.
В интервальном ряду распределения медиана рассчитывается по формуле:
, (3.26)
где 
- начало медианного интервала,
– длина медианного интервала,
|
|
|
– сумма накопленных частот до интервала, в котором находится медиана,
– частота медианного интервала.
К показателям структуры относятся квантили.
Квантили — это показатели, которые делят вариационные ряды на равные по численности единиц части. Квартили делят упорядоченный вариационный ряд на четыре равные части: первый квартиль является значением, которого не превышают 25% единиц совокупности, второй квартиль - 50% (он совпадает с медианой), третий— 75%.
Квинтили делят упорядоченный вариационный ряд на пять равных частей, децили - на десять равных частей. Пятый децильсовпадает с медианой и вторым квартилем.
Перцентили делят упорядоченный вариационный ряд на сто равных частей.
Показатели вариации
Вариация - это изменчивость (колеблемость) значений признака у разных единиц статистической совокупности. Вариация признака, возникающая в результате действия всех влияющих на него факторов называется обшей, под влиянием существенных факторов – систематической.
Вариационный ряд – это ряд распределения, построенный по атрибутивному (качественному) признаку.Различаютдискретные и интервальные вариационные ряды. В дискретных рядах значения признаков являются прерывными величинами, в интервальных - заданы в виде интервалов.
Вариация влияет на однородность статистической совокупности. Чем выше вариация признака, тем меньше однородность статистической совокупности. Для оценки степени однородности статистической совокупности применяют абсолютные и относительные показатели вариации.
К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение (стандартное отклонение).
Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака:
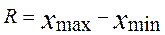(3.27)
Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от средней величины. Если ряд не сгруппирован, то рассчитывается простое среднее линейное отклонение:
|
|
|
(3.28)
Среднее квадратическое отклонение для несгруппированных данных рассчитывается по формуле:
(3.29)
для сгруппированных данных с неравными частотами:
(3.30)
Дисперсией (σ2) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней величины. Она равна Д= σ2
Дисперсия может быть рассчитана упрощенным способом как разность между средним значением квадратов индивидуальных значений признака и квадрата среднего значения этого же признака:
σ 2 = (Х2 ) - (Х) 2 (3.31)
Если совокупность единиц наблюдения разделена по какому-либо признаку на некоторое количество групп, то можно оценить зависимость вариации значений какого-либо показателя, характеризующую единицы наблюдения, от признака, положенного в основу группировки.
Общая дисперсия характеризует вариацию значений признака за счет всех факторов,как положенного в основу группировки, так и остальных не учтенных в группировке, но действующих на исследуемый признак.
Внутригрупповые дисперсии характеризуют вариацию значений исследуемого признака внутри групп независимо от того, какое значение принимает группировочный признак(оценивается влияние на показатель факторов, отличных от группировочного).
Мсжгрупповая дисперсия характеризует вариацию значений показателя за счет действия на него только группировочного признака.
Между средней из внутригрупповых дисперсий, межгрупповой и общей дисперсиями существует зависимость, известная как «правило сложения дисперсий»: общая дисперсия равна сумме межгрупповой и средней внутригрупповой.
Для сравнения вариации одного и того же показателя, но применительно к разным совокупностям, используют относительные показатели вариации. К ним относятся: коэффициент осцилляции, относительное линейное отклонение и 
коэффициент вариации. Если коэффициент вариации, выраженный в процентах, меньше 33% (по мнению некоторых авторов меньше 35- 40%), то статистическая совокупность считается однородной.
|
|
|
|
|
|
