Корреляционная связь и ее статистическое изучение

Введение

Целью курсовой работы является расчет обобщающих показателей, характеризующих закономерности исследуемых экономических явлений, и получение практических навыков в применении положений теории конкретных исследований.

 

Исходные данные

№ пред-приятия	Выпуск товаров и услуг в первом квартале текущего года, тыс. руб.	Среднесписочная численность работников, чел.	Средне-месячная стоимость ОПФ в марте, тыс. руб.
январь	февраль	март	февраль	март

 

 

Раздел 1.

Группировка статистических данных

 

 

xi
mi
∑ mi
xi
mi
∑ mi
xi
mi
∑ mi

 

Величина равных интервалов определяется по формуле:

 

∆

 

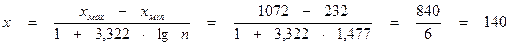
Результаты группировки и сводки излагаются в виде статистической таблицы.

Зависимость между размером предприятия

По стоимости ОПФ и выпуском товаров и услуг

табл.1

№ п/п	Группы предприятий по среднемесячной стоимости ОПФ, тыс. руб.	Количество предприятий	Выпуск товаров и услуг в целом по группе, тыс. руб.	Средний выпуск товаров и услуг, тыс.руб.	Изменение среднего выпуска товаров и услуг по сравнению с 1-ой группой, %
	232,00 – 372,50			703,00	100,00
	372,50 – 513,00			929,80	132,26
	513,00 – 653,50			1211,00	172,26
	653,50 – 794,00			1501,00	213,51
	794,00 – 934,50			1760,33	250,40
	934,50 – 1075,00			1852,38	263,50
Итого:

 

Раздел 2.

Ряды распределения

 

xi
mi
∑ mi
xi
mi
∑ mi
xi
mi
∑ mi

 

 

Формула Стерджисса:

 

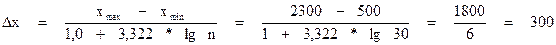
хначi-хконi	500,00 - 800,50	800,50 – 1101,00	1101,00 -1401,50	1401,50 -1702,00	1702,00 -2002,50	2002,50 -2303,00
хсрi	650,25	800,75	1251,25	1551,75	1952,25	2152,75
mi
∑ mi

 

 

Средняя арифметическая для дискретного ряда

 

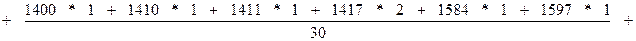
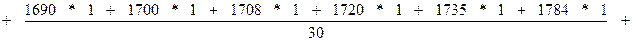
где x_i – варианты признака;

m_i – соответствующие частоты.

Средняя арифметическая для интервального ряда

 

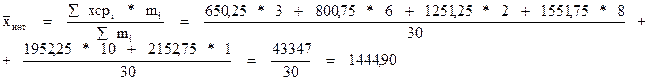
где х_срi – центр i-ого интервала;

m_i – частота в i-ом интервале

 

 

Мода и медиана

1) для дискретного ряда

При четном числе вариантов медиана будет равна средней арифметической из двух срединных вариантов.

 

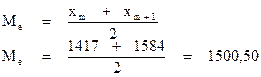
2) для интервального ряда

Медианным является первый интервал, для которого ∑m_i превышает половину от общего числа наблюдений. Т.е. интервал 1401,5 - 1702 – медианный.

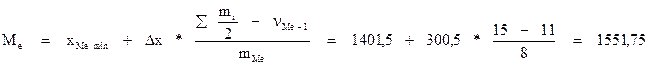
где х_Меmin – нижняя граница медианного интервала;

∆х – длина интервала;

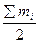- половина накопленных частот;

ν_m-1 – накопленная частота интервалов, предшествующая медианному интервалу

m_Me – частота медианного интервала.

 

Мода -это вариант, наиболее часто встречающийся в данном вариационном ряду.

 

1) для дискретного ряда – это вариант с наибольшей частотой.

М_о1 = 1417;

 

2) для интервального ряда определяют модальный интервал по наибольшей частоте (m_Мо = 10)

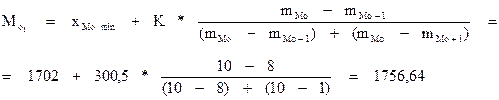
где х_Моmin – нижняя граница модального интервала;

К – величина интервала;

m_Мо – частота интервала;

m_Mo-1 – частота интервала, предшествующего модальному;

m_Mo+1 – частота интервала, следующего за модальным.

Показатели вариации

 

1. Размах вариации

 

R = x_max - x_min = 2300-500=1800

 

 

2. Среднее линейное отклонение (для интервального ряда).

 

 

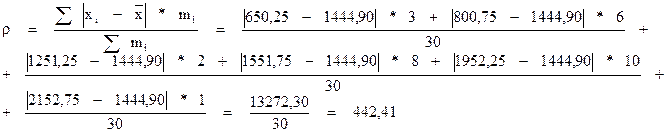
1. Дисперсия

 

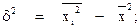
где 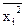- средняя из квадратов значений признака;

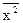- квадрат средней арифметической;

 

 

 

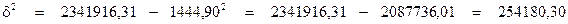
1. Среднее квадратичное отклонение

 

 

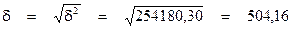
1. Коэффициенты вариации

 

 

 

 

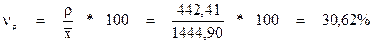
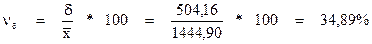
Раздел 3.

Дисперсия. Виды дисперсий

Закон сложения дисперсий

1. Общая дисперсия

 

,

где 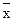- общая средняя для всей совокупности.

xi	mi	xi*mi
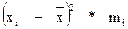
			904,7	818482,09
			903,7	816673,69
			811,7	658856,89
			591,7	350108,89
			584,7	341874,09
			576,7	332582,89
			572,7	327985,29
			486,7	236876,89
			304,7	92842,09
			214,7	46096,09
			4,7	22,09
			5,3	28,09
			6,3	39,69
			12,3	302,58
			179,3	32148,49
			192,3	36979,29
			285,3	81396,09
			295,3	87202,09
			303,3	91990,89
			315,3	99414,09
			330,3	109098,09
			379,3	143868,49
			387,3	150001,29
			397,3	157847,29
			407,3	165893,29
			500,3	250300,09
			515,3	265534,09
			537,3	288691,29
			895,3	801562,09
Итого:				6784698,30

 

 

1. Внутригрупповая дисперсия

 

где 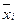- среднее значение признака в i-й группе;

- повторяемость отдельных значений признака в i-й группе.

 

 

1 группа

xi	fi	xi * fi
				12100,00
				12100,00
Итого:				24200,00

 

 

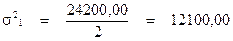
2 группа

xi	fi	xi * fi
			429,80	184728,04
			428,80	183869,44
			109,80	12056,04
			481,20	231553,44
			487,20	237363,84
Итого:				849570,80

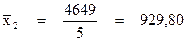
3 группа

xi	fi	xi * fi
			383,00	146689,00
			379,00	143641,00
			293,00	85849,00
			111,00	12321,00
			189,00	35721,00
			386,00	148996,00
			591,00	349281,00
Итого:				922498,00

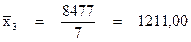
4 группа

xi	fi	xi * fi
			311,80	97219,24
			91,80	8427,24
			84,80	7191,04
			206,20	42518,44
			282,20	79636,84
Итого:				234992,80

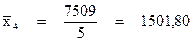
5 группа

xi	fi	xi * fi
			176,33	31092,27
			31,67	1002,99
			144,67	20929,41
Итого:				53024,67

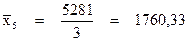
6 группа

xi	fi	xi * fi
			162,38	26367,26
			152,38	23219,66
			132,38	17524,46
			117,38	13778,06
			40,38	1630,54
			67,62	4572,46
			89,62	8031,74
			447,62	200363,66
Итого:				295487,88

 

 

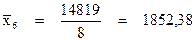
1. Средняя из внутригрупповых дисперсий

 

Средняя из внутригрупповых дисперсий рассчитывается как средняя арифметическая, взвешенная по численности отдельных групп:

 

 

где - абсолютный или относительный вес i-й группы в общей совокупности.

 

1. Межгрупповая дисперсия

 

 

 

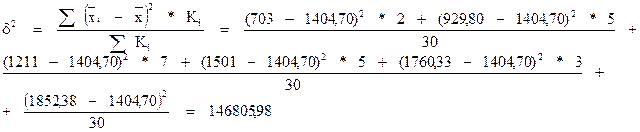
1. Закон сложения дисперсий

 

 

 

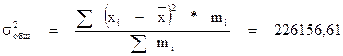
1. Коэффициент детерминации (корреляционное отношение)

 

 

 

Раздел 4.

Выборочное наблюдение

 

ü Определим среднюю стоимость ОПФ для всех предприятий отрасли в марте текущего года, гарантируя результат с вероятностью 0,954:

 

xi	mi	xi*mi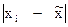
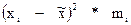
			487,66	237812,28
			423,66	179487,80
			324,66	105404,12
			266,66	71107,56
			262,66	68990,28
			254,66	64851,72
			220,66	48690,84
			183,66	33731,00
			175,66	30856,44
			129,66	16811,72
			126,66	16042,76
			123,66	15291,80
			87,66	7684,28
			83,66	6999,00
			63,66	4052,60
			47,66	2271,48
			7,66	117,36
			34,34	1179,24
			88,34	7803,96
			92,34	8526,68
			168,34	28338,36
			219,34	48110,04
			222,34	49435,08
			261,34	68298,60
			262,34	68822,28
			269,34	72544,04
			272,34	74169,08
			315,34	99439,32
			352,34	124143,48
Итого:			1561013,08

 

- выборочная средняя:

 

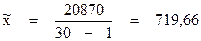
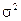- дисперсия признака в генеральной совокупности:

 

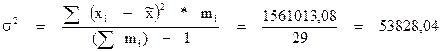
где n – объём выборки:

n = 30 предприятий.

N – объём генеральной совокупности:

N=n/0,2 = 30/0,2 = 150 предприятий.

t - коэффициент доверия, связанный с гарантийной вероятностью P:

.

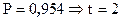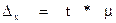- предельная ошибка средней;

 

 

Доверительные интервалы для генеральной средней :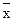

с вероятностью P.

Т.о., доверительные интервалы для генеральной средней равны:

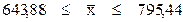с вероятностью P=0,954.

 

Определим вероятность того, что средняя стоимость ОПФ отличается от полученной по выборке не более, чем на 100 тыс.руб.

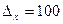тыс.руб.

 

По таблице ([3] Приложение 3) определяем доверительную вероятность:

 

t=2,64 P=0,9917

 

 

Вывод:

 

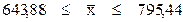c P = 0,954 - средняя стоимость ОПФ для всех предприятий. Вероятность того, что средняя стоимость ОПФ отличается от полученной по выборке не более, чем на 100 тыс. руб. равна Р = 0,9917.

 

Раздел 5.

Корреляционная связь и ее статистическое изучение

 

Y - производительность труда (выпуск товаров и услуг на одного рабочего.

X – уровень вооруженности труда ОПФ (стоимость ОПФ на одного рабочего).

 

№ предприятия	Выпуск товаров и услуг в марте, тыс.р.	Среднемесячная стоимость ОПФ в марте	Среднеспи-сочная численность работников в марте, чел.	Среднеме-сячная стоимость ОПФ в марте на одного работника (х)	Выпуск товаров и услуг в марте на одного работника, тыс.р. (у)
				6,47	16,22
				8,08	19,05
				5,67	14,58
				6,45	18,39
				5,38	16,60
				2,97	7,60
				5,83	17,36
				3,84	10,56
				5,39	16,87
				6,85	16,42
				7,74	10,81
				10,09	17,24
				8,00	14,17
				5,98	7,58
				8,72	16,78
				7,94	14,84
				9,99	18,30
				9,81	17,35
				9,24	17,14
				8,24	11,50
				8,92	17,41
				6,65	10,93
				7,81	16,87
				9,54	16,35
				8,22	16,59
				6,94	7,48
				7,47	13,92
				8,25	17,69
				8,77	17,34
				8,37	12,08

 

Берём 6 групп по Х_i и 6 групп по У_i

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: