Главная | Обратная связь | Поможем написать вашу работу!

Макет корреляционной таблицы

Интерва-лы х_i	Интервалы у_i	Число наб-людений mi	Средн. знач. у_i в данном интервале по х_i
7,48- 9,41	9,41- 11,13	11,13- 13,27	13,27- 15,20	15,20- 17,13	17,13-19,06
2,97 - 4,16	7,60	10,56					9,08
4,16 - 5,35
5,35 - 6,54	7,58			14,58	16,22 16,60 16,87	18,39 17,36	15,37
6,54 - 7,73	7,48	10,93		13,92	16,42		12,19
7,73 - 8,92		10,81	11,50 12,08	14,17 14,84	16,78 16,87 16,59	19,05 17,69 17,34	15,25
8,92 – 10,11					16,35	17,24 18,30 17,35 17,14 17,41	17,30
Число наблюде-ний

Вспомогательная таблица для расчёта сумм слагаемых в системе уравнений

№ n/n	x_i	y_i	x_i²	y_i²	y_i*x_i
	6,47	16,22	41,86	263,09	104,94	13,92
	8,08	19,05	65,29	362,90	153,92	15,48
	5,67	14,58	32,15	212,58	82,67	13,14
	6,45	18,39	41,60	338,19	118,62	13,90
	5,38	16,60	28,94	275,56	89,31	12,86
	2,97	7,60	8,82	57,76	22,57	10,52
	5,83	17,36	33,99	301,37	101,21	13,30
	3,84	10,56	14,75	111,51	40,55	11,36
	5,39	16,87	29,05	284,60	90,93	12,87
	6,85	16,42	46,92	269,62	112,48	14,28
	7,74	10,81	59,91	116,86	83,67	15,15
	10,09	17,24	101,81	297,22	173,95	17,43
	8,00	14,17	64,00	200,79	113,36	15,40
	5,98	7,58	35,76	57,46	45,33	13,44
	8,72	16,78	76,04	281,57	146,32	16,10
	7,94	14,84	63,04	220,23	117,83	15,34
	9,99	18,30	99,80	334,89	182,82	17,33
	9,81	17,35	96,24	301,02	170,20	17,16
	9,24	17,14	85,38	293,78	158,37	16,60
	8,24	11,50	67,90	132,25	94,76	15,63
	8,92	17,41	79,57	303,11	155,30	16,29
	6,65	10,93	44,22	119,46	72,68	14,09
	7,81	16,87	61,00	284,60	131,75	15,22
	9,54	16,35	91,01	267,32	155,98	16,89
	8,22	16,59	67,57	275,23	136,37	15,61
	6,94	7,48	48,16	55,95	51,91	14,37
	7,47	13,92	55,80	193,77	103,98	14,89
	8,25	17,69	68,06	312,94	145,94	15,64
	8,77	17,34	76,91	300,68	152,07	16,15
	8,37	12,08	70,06	145,93	101,11	15,76
Итого:	223,62	446,02	1755,60	6972,21	3410,91	446,11

Линейная зависимость:

Система «нормальных» уравнений имеет вид:

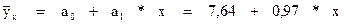
x_i	m_i	x _i* m_i			у_i	m_i	у_i * m_i
6,47		6,47	0,98	0,96	16,22		16,22	1,35	1,82
8,08		8,08	0,63	0,40	19,05		19,05	4,18	17,47
5,67		5,67	1,78	3,17	14,58		14,58	0,29	0,08
6,45		6,45	1,00	1,00	18,39		18,39	3,52	12,39
5,38		5,38	2,07	4,28	16,60		16,60	1,73	2,99
2,97		2,97	4,48	20,07	7,60		7,60	7,27	52,85
5,83		5,83	1,62	2,62	17,36		17,36	2,49	6,20
3,84		3,84	3,61	13,03	10,56		10,56	4,31	18,58
5,39		5,39	2,06	4,24	16,42		16,42	1,55	2,40
6,85		6,85	0,60	0,36	10,81		10,81	4,06	16,48
7,74		7,74	0,29	0,08	17,24		17,24	2,37	5,62
10,09		10,09	2,64	6,97	14,17		14,17	0,70	0,49
8,00		8,00	0,55	0,30	7,58		7,58	7,29	53,14
5,98		5,98	1,47	2,16	16,78		16,78	1,91	3,65
8,72		8,72	1,27	1,61	14,84		14,84	0,03	0,00
7,94		7,94	0,49	0,24	18,30		18,30	3,43	11,76
9,99		9,99	2,54	6,45	17,35		17,35	2,48	6,15
9,81		9,81	2,36	5,57	17,14		17,14	2,27	5,15
9,24		9,24	1,79	3,20	11,50		11,50	3,37	11,36
8,24		8,24	0,79	0,62	17,41		17,41	2,54	6,45
8,92		8,92	1,47	2,16	10,93		10,93	3,94	15,52
6,65		6,65	0,80	0,64	16,87		33,74	2,00	8,00
7,81		7,81	0,36	0,13	16,35		16,35	1,48	2,19
9,54		9,54	2,09	4,37	16,59		16,59	1,72	2,96
8,22		8,22	0,77	0,59	7,48		7,48	7,39	54,61
6,94		6,94	0,51	0,26	13,92		13,92	0,95	0,90
7,47		7,47	0,02	0,00	17,69		17,69	2,82	7,95
8,25		8,25	0,80	0,64	17,34		17,34	2,47	6,10
8,77		8,77	1,32	1,74	12,08		12,08	2,79	7,78
8,37		8,37	0,92	0,85
Итого:		223,62		88,74			446,02		341,08

Линейный коэффициент корреляции:

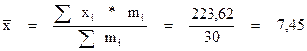
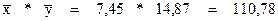
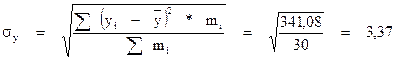
Оценка значимости линейного коэффициента корреляций осуществляется по формуле:

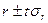
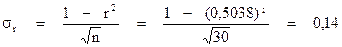
Kоэффициент корреляции

у_i
16,22	13,92	5,29
19,05	15,48	12,74
14,58	13,14	2,07
18,39	13,90	20,16
16,60	12,86	13,99
7,60	10,52	8,53
17,36	13,30	16,48
10,56	11,36	0,64
16,87	12,87	16,00
16,42	14,28	4,58
10,81	15,15	18,84
17,24	17,43	0,04
14,17	15,40	1,51
7,58	13,44	34,34
16,78	16,10	0,46
14,84	15,34	0,25
18,30	17,33	0,94
17,35	17,16	0,04
17,14	16,60	0,29
11,50	15,63	17,06
17,41	16,29	1,25
10,93	14,09	9,99
16,87	15,22	2,72
16,35	16,89	0,29
16,59	15,61	0,96
7,48	14,37	47,47
13,92	14,89	0,94
17,69	15,64	4,20
17,34	16,15	1,42
12,08	15,76	13,54
Итого: 446,02		257,04

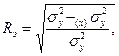
где - дисперсия фактора Y;

- дисперсия Y под действием всех факторов, кроме Х:

где - фактическое значение фактора Y;

- выравнивание по Х значения результативного показателя;

- показывает относительное значение вариации под действие фактора Х в общей вариации.

В качестве меры достоверности уравнения корреляционной зависимости используется процентное отношение средней квадратической ошибки уравнения (S) к среднему уровню результативного признака ():

где - фактические значения результативного признака;

- значения результативного признака, рассчитанные по уравнению регрессии;

l – число параметров в уравнении регрессии (в случае линейной зависимости l = 2).

Вывод:

1) По корреляционной таблице можно предположить, что связь прямая.

2) При значениях показателей тесноты связи R = 0,50 и r = 0,50 зависимость результативного признака от факторного является умеренной.

Раздел 6.

Индексы

где 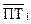и — средний уровень производительности труда па группе предприятий соответственно в отчетном и базисном периодах.

Средний уровень производительности труда по группе предприятий исчисляется по формулам средней арифметической взвешенной:

; ,

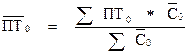где ПТ₀ и ПТ₁ — производительность труда по каждому предприятию соответственно в базисном и отчетном периодах;

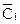и — среднесписочное число работников по каждому предприятию соответственно в базисном и отчетном периодах.

Следовательно, индекс переменного состава примет вид:

Величины 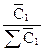и 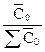отражают структуру явления, т.е. распределение работников по предприятиям, а формула может быть записана следующим образом:

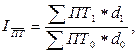
где и 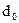- удельный вес каждого предприятия в общей численности работников группы предприятий соответственно в отчётном и базисном периодах.

Составим вспомогательную таблицу

№ предприятия	Февраль	Март

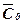
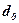
			15,75	0,23			18,39	0,23
			13,58	0,20			16,60	0,20
			7,56	0,17			7,60	0,18
			15,81	0,22			17,36	0,21
			10,36	0,18			10,56	0,18
Итого:	5683,00	438,00	63,07	1,00	6216,00	430,00	70,51	1,00

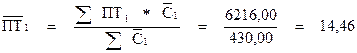
№ предприятия	Февраль	Март

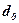
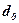
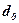
	15,75	0,23	18,39	0,23	3,62	3,62	4,23	4,23
	13,58	0,20	16,60	0,20	2,72	2,72	3,32	3,32
	7,56	0,17	7,60	0,18	1,29	1,36	1,29	1,37
	15,81	0,22	17,36	0,21	3,48	3,32	3,82	3,65
	10,36	0,18	10,56	0,18	1,86	1,86	1,90	1,90
Итого:	63,07	1,00	70,51	1,00	12,97	12,88	14,56	14,46

Индекс переменного состава:

Абсолютное изменение средней производительности труда по группе предприятий:

Индекс фиксированного состава:

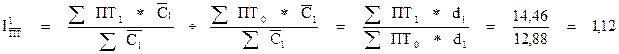
Абсолютное изменение средней производительности труда по группе предприятий за счет изменения производительности труда по предприятиям:

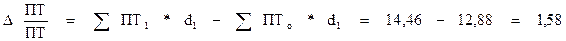
Индекс влияния структурных сдвигов в распределении работников определяется по формуле:

Абсолютное изменение средней производительности труда по группе предприятий за счет структурных сдвигов в распределении работников по предприятиям:

Поскольку изменение средней производительности труда по группе предприятий определяется изменением двух факторов, то

Абсолютный прирост выпуска товаров и услуг по группе предприятий в текущем месяце по сравнению с предыдущим, получен за счёт двух факторов:

а) изменения численности работников:

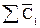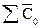где и - среднесписочная численность работников по группе предприятий в отчётном и базисном периодах.

б) изменения производительности труда:

Абсолютный прирост выпуска товаров и услуг по группе предприятий равен:

где и - суммарный выпуск товаров и услуг по группе предприятий соответственно в отчётном и базисном периодах.

Раздел 7.

Ряды динамики

где ; ; … .

Отсюда:

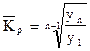Темп роста – это коэффициент роста, выраженный в процентах. Средний темп роста определяется только через средний коэффициент роста:

Темп прироста – это отношение (в виде коэффициента или в процентах) абсолютного прироста к предыдущему уровню ряда.

Темп прироста можно рассчитать по формуле:

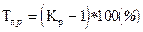или .

Средний темп прироста определяется по среднему коэффициенту роста либо по среднему темпу роста:

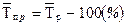
Абсолютное значение 1% прироста – это отношение абсолютного прироста к темпу прироста, рассчитанным для одного и того же периода. Соответствующая средняя величина определяется по формуле:

№ предприятия	Выпуск товаров и услуг в первом квартале текущего года, тыс руб.
январь	февраль	март































Итого

Вычислим показатели динамики выпуска товаров и услуг в целом по всей группе 30-ти предприятий от месяца к месяцу:

Наименование показателя	Месяц
январь	февраль	март
Абсолютный прирост ∆, тыс.руб	с переменной базой	-
с постоянной базой	-
Коэффициент роста К_р	с переменной базой	-	1,04	1,05
с постоянной базой	-	1,04	1,09
Темп роста Т_р, %	с переменной базой	-
с постоянной базой	-
Темп прироста , %	с переменной базой	-
с постоянной базой	-
Абсолютное значение 1 % прироста, А	с переменной базой	-	403,75	396,80
с постоянной базой	-	403,75	399,89

1) Средний уровень интервального ряда

2) Средний абсолютный прирост:

3) Средний коэффициент роста

4) Средний темп роста

5) Средний темп прироста

6) Среднее абсолютное значение 1 % прироста

⇐ Предыдущая 12

Воспользуйтесь поиском по сайту: