Гидростатическим давлением называется нормальная составляющая вектора напряжения от действия поверхностной силы, действующей в любой точке жидкости.

Методика выполнения лабораторных работ по гидравлике

в оболочке виртуальной лаборатории…………………….…………..….......3

 

Лабораторная работа № 1. Измерение гидростатического давления

и экспериментальное подтверждение закона Паскаля….………..…….….. 5

 

Лабораторная работа № 2.Экспериментальная иллюстрация

и расчетное определение ламинарного и турбулентного режимов

движения жидкости ………….…………………………………………….....15

 

Лабораторная работа № 3.Определение опытным путем величин

слагаемых уравнения Д. Бернулли при установившемся

неравномерном движении жидкости в трубопроводе…..….……………...27

 

Лабораторная работа № 4. Определение значений коэффициентов

гидравлического сопротивления и гидравлических потерь

напора при движении жидкости в трубопроводе……….…………………..34

 

Лабораторная работа № 5. Изучение истечения жидкости через

малые отверстия в тонкой стенке и насадки в атмосферу

при постоянном напоре ……………………………………….……………..41

 

Лабораторная работа № 6. Экспериментальное изучение прямого

гидравлического удара в трубопроводе…………………………………. 49

 

 

Введение

Методические указания предназначены бакалавров по направлению подготовки 110800.62 Агроинженерия очного и заочного обучения при подготовке к лабораторным занятиям по дисциплине Гидравлика.

Материалы, изложенные в работе, способствуют формированию у студентов профессиональных компетенций направления подготовки 110800.62 Агроинженерия.

Научную базу современной гидравлики составляют общие законы механики, полученные при изучении курсов физики и теоретической механики, а также разделов математики.

Теоретическое изучение дисциплины «Гидравлика» сопровождается практическими занятиями, лабораторными работами, самостоятельным выполнением расчетно-графических и курсовой работ.

При изучении курсов Гидравлика, «Гидромеханика» и для решения многих практических задач механики жидкости и газа необходимо иметь опыт проведения экспериментальных исследований, связанных с таким движением жидкости, которое не поддаётся теоретической схематизации. Например, с потоками в некоторых местных сопротивлениях и в каналах гидравлических машин. Для этой цели и предназначен лабораторный комплекс в виртуальной оболочке.

Методические указания содержат основные теоретические положения и сведения для выполнения лабораторных работ, а также контрольные вопросы и источники литературы по соответствующей тематике.

Методика выполнения лабораторных работ

По гидравлике в оболочке виртуальной лаборатории

Лабораторный комплекс состоит из шести лабораторных установок. Все установки представляют собой мультипликационное изображение на экране дисплея и математической модели действующих установок изучаемого физического процесса.

Программа позволяет имитировать измерения параметров физического процесса с помощью приборов, применяемых в практике гидравлического эксперимента: пьезометров, манометров, вакуумметров для измерения гидростатического напора; трубки Пито и датчиков скорости для измерения скоростного напора; мерные емкости и секундомеры для определения объемного расхода жидкости.

Методики выполнения лабораторных работ в оболочке компьютерной лаборатории предусматривают изучение теории физического явления, ознакомление с устройством и принципом действия экспериментальной установки, формулирование целей, задач и порядка выполнения работы. Обработка результатов измерений и вычисления параметров эксперимента выполняются в табличной форме по формулам и уравнениям, приведенным в практикуме для соответствующей работы.

В соответствии с выполняемой работой

─ изучаются теоретические основы выбранной работы, описание и принцип действия лабораторной установки или стенда, цель и порядок выполнения экспериментов, формы таблиц для записи и обработки получаемых данных, основные расчетные формулы и контрольные вопросы.

─ оформляется протокол выполняемой работы по следующей форме. Название, фамилия имя отчество и номер группы студента; цель выполняемой работы, схема экспериментальной установки и порядок выполнения работы; основные расчетные формулы, необходимые для расчета; результаты измерений и вычислений, представленные в таблицах соответствующей формы, приведенных в руководстве по выполняемой работе; вывод по работе.

При выполнении работы необходимо:

- войти в меню настройки лабораторной установки, ознакомиться при необходимости с информацией по лабораторному стенду и произвести выбор постоянных параметров в соответствии с заданием преподавателя;

- включить режим выполнения лабораторной работы, произвести измерения необходимых параметров и внести полученные данные в таблицу протокола. Повторить измерения в других режимах с цель получения достаточного количества данных для анализа изучаемого явления или построения характеристик гидравлических машин и гидроприводов;

- выйти из программы, обработать результаты измерений, построить необходимые графики и характеристики, сделать вывод по выполненной лабораторной работе и представить её к защите преподавателю.

Лабораторная работа № 1

Измерение гидростатического давления.

Экспериментальное подтверждение закона Паскаля

Цель работы: Экспериментальное подтверждение закона Паскаля.

Общие сведения

1.1 Силы, действующие в жидкости, можно разделить на две группы:

─ объёмные (массовые) силы действуют на каждую частицу, находящуюся в рассматриваемом объёме.

Примерами таких сил являются силы тяжести, инерции, электростатические и т. п.

─ поверхностные силы действуют на элементы поверхности, ограничивающей выделенный объём.

К ним относятся силы давления и трения, обусловленные вязкостью жидкости.

При описании силовых взаимодействий в жидкостях, в отличие от твердых тел, имеют дело не с самими силами, а с их плотностями.

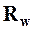Плотностью распределения объемных сил в данной точке среды называют предел отношения главного вектора объёмных сил , приложенного к точке, расположенной внутри малого объёма , к массе этого объёма при условии, что объём стремиться к нулю, т.е.

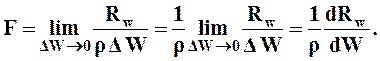(1.1)

В системе СИ плотность объемных сил имеет размерность м/с².

Плотности объёмных сил изменяются в пространстве и времени

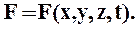
В проекциях на оси координат вектор плотности объёмных сил представляют в следующем виде

(1.2)

Вектор напряжений поверхностных сил равен пределу отношения главного вектора поверхностных сил к площади , на которую он действует, при условии, что величина этой площади стремиться к нулю

(1.3)

Индекс у вектора напряжения указывает на конкретную площадку, заданную нормалью , в пределах которой действуют рассматриваемые напряжения.

Гидростатическим давлением называется нормальная составляющая вектора напряжения от действия поверхностной силы, действующей в любой точке жидкости.

За единицу измерения гидростатического давления принят Паскаль ─ равномерно распределённое давление, создаваемое силой в 1Н на площади в 1м².

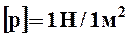(один Паскаль).

1.2 Основным дифференциальным уравнением равновесия жидкости является уравнение Эйлера.

Общая форма уравнения равновесия жидкости имеет вид

(1.4)

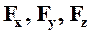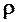где ─ проекции плотностей распределения объёмных сил на оси координат , м/с²; ─ плотность жидкости, кг/м³.

С учетом единичных векторов ─ координатных осей , суммируя все члены системы 1.4, получим уравнение

которое можно записать в векторной форме

(1.5)

Умножив каждое уравнение системы 1.4 соответственно на 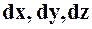, и суммируя их, получим третью форму уравнения равновесия жидкости

. (1.6)

1.3 Левая часть уравнения 1.6 представляет полный дифференциал 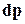функции и для однородной несжимаемой жидкости , тогда в правой части уравнения 1.6 выражение в скобках ─ полный дифференциал некоторой функции 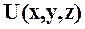, т.е.

или

Следовательно, поле массовых сил потенциальное (минус U - потенциал).

Уравнение 1.5 можно представить в виде

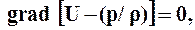
интеграл которого равен

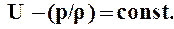(1.7)

Уравнение 1.7 является общей формой интеграла уравнений гидростатики, в случае, когда объёмные силы имеют потенциал.

1.4 В общем случае равновесия жидкости действует только одна объёмная сила ─ сила тяжести

В случае действия на жидкость только силы тяжести, плотность объёмных сил тяжести равна ускорению свободного падения

Направив ось вертикально вверх, получим

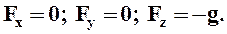
Подставив полученные величины в уравнение 1.6, будем иметь

Интегрируя это уравнение, получим

или

где ─ постоянная интегрирования.

Разделив обе части этого уравнения на 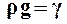, где ─ удельный вес данной жидкости, запишем это уравнение в следующем виде

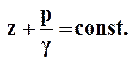(1.8)

Уравнение 1.8 является законом распределения гидростатического давления (основное уравнение гидростатики).

Из уравнения 1.8 следует, что для свободной поверхности (рисунок 1.1), координата которой равна и давление , можно записать

─ гидростатический напор

или

(1.9)

где ─ весовое давление, давление обусловленное весом жидкости, которое также называется избыточным, относительным или манометрическим; ─ глубина заглубления, равная (рисунок 1.1).

Абсолютное давление в любой точке жидкости равняется сумме внешнего давления 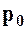и избыточного давлений ─ основной закон гидростатики.

В случае изменения внешнего давления 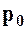на некоторую величину, на эту же величину изменяется давление во всех точках жидкости – закон Паскаля.

 

Рисунок 1.1─ Геометрическое пояснение основного уравнения

гидростатики

 

На практике рассчитывают не абсолютное давление, а его отклонение от атмосферного – .

Если 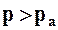, то избыточное давление равно .

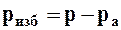Если 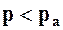, то недостаток давления до атмосферного называют вакуумом. В этом случае .

Абсолютное давление не может быть отрицательным, так как жидкость не выдерживает растягивающих напряжений. Избыточное давление может быть как положительным так и отрицательным.

В гидравлических расчётах величину нормального атмосферного давления считают равной =98100 Па.

1.5 Приборы, применяемые для измерения

По принципу действия приборы для измерения делятся на две группы: жидкостные и деформационные (механические).

Жидкостные приборы ─ пьезометры, представляют собой стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединён к точке, где измеряется манометрическое давление. Показания пьезометра определяет избыточное давление

, (1.10)

где ─ удельный вес жидкости;

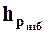─ пьезометрическая высота, т.е. высота, отсчитываемая от точки подключения пьезометра до уровня жидкости в нём.

Действие механических приборов - манометров, основано на деформации под действием давления упругого элемента (пружины или мембраны). Манометр показывает давление в точке жидкости на уровне оси вращения его стрелки прибора. Если высотное положение оси вращения стрелки и точки подключения манометра не совпадает (рисунок 1.2), то в показание манометра () вводят поправку ().

Для случая, изображённого на рисунке 1.2

, (1.11)

где 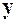─ превышение оси вращения стрелки манометра над точкой его подключения, м.

 

1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: