 |
Описание установки и методика выполнения работы
|
|
|
|
2.1 Установка (рисунок 4.3) представляет собой систему напорных трубопроводов с последовательно расположенными на нем гидравлическими сопротивлениями (по длине и местными).
 |
Рисунок 4.3 ─ Схема установки
К каждому гидравлическому сопротивлению подключено по два пьезометра (перед и за ним). Все пьезометры для удобства работы выведены на щит 4. Для регулирования расхода воды  в системе служит вентиль 2. Величина
в системе служит вентиль 2. Величина  измеряется с помощью мерного бака 1 и секундомера. 3. Подача воды в систему осуществляется из питающего резервуара 5 по трубе открытием задвижки. Постоянный уровень воды в резервуаре 5 (для обеспечения установившегося движения в системе) поддерживается переливным устройством. Вода в резервуар 5 подается центробежным насосом.
измеряется с помощью мерного бака 1 и секундомера. 3. Подача воды в систему осуществляется из питающего резервуара 5 по трубе открытием задвижки. Постоянный уровень воды в резервуаре 5 (для обеспечения установившегося движения в системе) поддерживается переливным устройством. Вода в резервуар 5 подается центробежным насосом.
2.2 При закрытом вентиле 2 включить насос и обеспечить подачу воды в питающий резервуар 5. После наполнения водой резервуара и стабилизации уровня воды в нем (переливное устройство должно при этом работать) следует плавным открытием вентиля 2 подать воду в систему трубопроводов. Далее, необходимо измерить: отметки уровней воды в пьезометрах, расход воды в системе (с помощью мерного бака 1 и секундомера 3), а так же ее температуру (термометром в резервуаре 1). Результаты измерений для опытов (при разных расходах воды) записать в таблицу 4.1.
Таблица 4.1 - Результаты измерений и расчета
| № | Наименование измеряемых и вычисляемых величин | Участок прямой трубы 1 | Участок прямой трубы 2 | Внезапное сужение потока | Внезапное расшир. потока | Участок прямой трубы 3 | |||||
| Номера сечений | |||||||||||
Диаметр трубы,  , м , м
| |||||||||||
| Площадь сечения, S=p D2/4, м2 | |||||||||||
| Показания пьезометра (отметка уровня воды в нем),м | |||||||||||
Мерный объём жидкости,
 , м3 , м3
| |||||||||||
Время наполнения мерного объёма,  , с , с
| |||||||||||
Температура воды,  , °С , °С
| |||||||||||
Длина участка прямой
трубы, 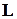 , м , м
| |||||||||||
Расход воды,  , м3 , м3
| |||||||||||
Скоростной напор в сечении  , м , м
| |||||||||||
Полный напор в сечении, м

| |||||||||||
Местные потери напора,
 , м , м
| |||||||||||
Потери по длине,  , м , м
|
Продолжение таблицы 4.1
|
|
|
Опытный коэффициент
местных потерь, 
| |||||||||||
Справочный коэффициент местных потерь, 
| |||||||||||
Число Рейнольдса 
| |||||||||||
Опытный коэффициент гидравлического трения, 
| |||||||||||
| Расчетный коэффициент гидравлич. трения, λрас |
Обработать опытные данные и результаты представить в виде таблицы 4.1. Сформулировать выводы по результатам работы.
3 Основные контрольные вопросы
1. Напишите и поясните формулы Дарси-Вейсбаха и Вейсбаха.
2. Поясните, как опытным путем определяют величины коэффициентов l и x.
3. Что характеризуют коэффициенты l и x, от каких факторов в общем случае они зависят и как их определяют при гидравлических расчетах?
|
|
|
4. Объясните, что такое Dэ и Dэ/d, как найти величину Dэ при гидравлических расчетах.
5. Назовите области гидравлического сопротивления трубопроводов и объясните, как определяют область сопротивления при гидравлических расчетах.
6. Изобразите схемы движения жидкости при резком повороте трубы на 900, а также при резком расширении и резком сужении трубопровода и дайте пояснения к ним, указав, что характерно для движения потока при протекании его через любое местное сопротивление.
Лабораторная работа № 5
Изучение истечения жидкости через малые отверстия в тонкой
Стенке и насадки при постоянном напоре в атмосферу
Цель работы: Исследование параметров истечения через малое круглое отверстие и из внешнего цилиндрического и конических (сходящегося и расходящегося) насадков при постоянном напоре в атмосферу.
Общие сведения
Гидравлически малым отверстием считают отверстие, высота которого не превышает 0,1 Н, где Н ─ превышение свободной поверхности жидкости над центром тяжести отверстия. Стенку считают тонкой, если ее толщина d < (1,5...3,0)d, где d ─ диаметр отверстия. При выполнении этого условия величина d не влияет на характер истечения жидкости из отверстия, так как вытекающая струя жидкости касается только острой кромки отверстия.
Поскольку частицы жидкости движутся к отверстию по криволинейным траекториям, под действием сил инерции струя, вытекающая из отверстия, сжимается. Благодаря действию сил инерции струя продолжает сжиматься и после выхода из отверстия. Наибольшее сжатие струи, как показывают опыты, наблюдается в сечении «с-с» на расстоянии примерно (0,5...1,0)d от входной кромки отверстия (рисунок 5.1). Это сечение называют сечением сжатия.
Степень сжатия струи в этом сечении оценивают коэффициентом сжатия e:
 , (5.1)
, (5.1)
 где wс и w соответственно площадь сжатого живого сечения струи и площадь отверстия.
где wс и w соответственно площадь сжатого живого сечения струи и площадь отверстия.
Рисунок 5.1─ Истечение жидкости из отверстия в тонкой стенке
Среднюю скорость струи Vc в сечении сжатия с-с при  вычисляют по формуле, полученной из уравнения Д. Бернулли, составленного для сечений 1-1 и с-с (рисунок 5.1):
вычисляют по формуле, полученной из уравнения Д. Бернулли, составленного для сечений 1-1 и с-с (рисунок 5.1):
|
|
|
 , (5.2)
, (5.2)
где j ─ коэффициент скорости отверстия
 (5.3)
(5.3)
На основе использования уравнения траектории струи, вытекающей из отверстия, получено еще одно выражение для коэффициента j:
 (5.4)
(5.4)
В формулах(5.2) и(5.4) a ─ коэффициент Кориолиса, z ─ коэффициент сопротивления отверстия, xi и yi ─ координаты произвольно взятой точки траектории струи.
Поскольку напор теряется главным образом вблизи отверстия, где скорости достаточно велики, при истечении из отверстия во внимание принимают только местные потери напора.
Расход жидкости Q через отверстие равен:
 (5.5)
(5.5)
где  , (5.6)
, (5.6)
m ─ коэффициент расхода отверстия, учитывающий влияние гидравлического сопротивления и сжатия струи на расход жидкости. С учетом выражения для m формула (5.5) принимает вид
 (5.7)
(5.7)
Величины коэффициентов e, z, j, m для отверстий определяют опытным путем. Установлено, что они зависят от формы отверстия и числа Рейнольдса. Однако при больших числах Рейнольдса (Re ³ 105) указанные коэффициенты от Re не зависят и для круглых и квадратных отверстий при совершенном сжатии струи равны: e= 0,62...0,64, z=0,06, j=0,97...0,98, m=0,60...0,62.
Насадкой называют патрубок длиной 2,5d £ LH £ 5d (рисунок 5.2), присоединенный к малому отверстию в тонкой стенке с целью изменения гидравлических характеристик истечения (скорости, расхода жидкости, траектории струи).
Насадки бывают цилиндрические (внешние и внутренние), конические (сходящиеся и расходящиеся) и коноидальные, т.е. очерченные по форме струи, вытекающей из отверстия.
Использование насадки любого типа вызывает увеличение расхода жидкости Q благодаря вакууму, возникающему внутри насадка в области сжатого сечения с-с (рисунок 5.2) и обуславливающему повышение напора истечения.
Среднюю скорость истечения жидкости из насадки V и расход Q определяют по формулам, полученным из уравнения Д. Бернулли, записываемого для сечений 1-1 и 3-3 (рисунок 5.2).
 , (5.8)
, (5.8)
 где
где  ─ коэффициент скорости насадки; zН ─ коэффициент сопротивления насадки.
─ коэффициент скорости насадки; zН ─ коэффициент сопротивления насадки.
Рисунок 5.2 ─ Истечение из внешнего цилиндрического насадка
|
|
|
Для выходного сечения 3-3 коэффициент сжатия струи e=1 (насадка в этой области работает полным сечением), поэтому коэффициент расхода насадки mН = jН.
Расход жидкости, вытекающий из насадки, вычисляется по формуле, аналогичной формуле (5.7),
 (5.9)
(5.9)
|
|
|


