 |
Математическая модель движения самолета
|
|
|
|
Полёт самолёта осуществляется под влиянием сил и моментов, действующих на него. Отклоняя органы управления, лётчик может регулировать величину и направление сил и моментов, а соответственно изменять параметры движения самолета в желаемую сторону. Для прямолинейного и равномерного полёта необходимо, чтобы все силы и моменты были уравновешены, сбалансированы. Так, например, в горизонтальном прямолинейном полёте с постоянной скоростью подъемная сила равна силе тяжести самолёта, а тяга двигателя – силе лобового сопротивления. При этом обязательно должно соблюдаться я равновесие моментов. В противном случае самолет начинает вращаться. Равновесие, созданное летчиком, может быть нарушено воздействием какого-либо возмущающего фактора, например, турбулентностью атмосферы или порывами ветра. Поэтому когда режим полета установлен, то требуется обеспечить устойчивость движения. Другой важнейшей характеристикой самолета является управляемость. Под управляемостью самолета понимают его способность реагировать на перемещения рычагов управления (органов управления). О хорошо управляемом самолете летчики говорят, что он хорошо «ходит за ручкой». Это означает, что для выполнения требуемых маневров лётчику необходимо совершить простые по характеру отклонения рычагов и прилагать к ним небольшие до величине, но чётко ощутимые усилия, на которые самолет отвечает соответствующими изменениями положения в пространстве без излишнего запаздывания. Управляемость – важнейшая характеристика самолета, определяющая возможность полета. На неуправляемом самолете летать невозможно. Лётчику одинаково трудно управлять самолётом, когда требуется прикладывать большие усилия к рычагам управления и выполнять большие перемещения штурвала, а также когда отклонения штурвала и усилия, потребные для их отклонения, слишком малы. В первом случае лётчик быстро утомляется при совершении маневров. О таком самолёте говорят, что он «тяжёл в управлении». Во втором случае самолёт реагирует на малое, иногда даже непроизвольное перемещение ручки, требуя от лётчика большого внимания, точного и плавного управления. О таком самолёте говорят, что он «строг в управлении». Требуется разработать алгоритм ручного управления самолетом, который удовлетворяет требованиям удобного и безопасного пилотирования, а также требованиям к статическим и динамическим характеристикам и разбросу параметров. При рассмотрении углового движения самолета обычно рассматривают связанную и полусвязанную системы координат (Рис.2.). За начало координат принимается точка, в которой расположен центр тяжести самолета. Ось OX проводится параллельно хорде крыла и называется продольной осью самолета. Нормальная ось OY перпендикулярна оси OX и расположена в плоскости симметрии самолета. Ось OZ перпендикулярна к осям OX и OY, а следовательно, и к плоскости симметрии самолета. Она называется поперечной осью самолета. Координатная система OXYZ называется связанной.
|
|
|
Рисунок 2 – Системы координат, основные силы и моменты при продольном движении. Вместе со связанной системой координат вводят полусвязанную систему координат. Ось OX1 в этой системе направляют по вектору скорости самолета. ОсьOY1 направлена перпендикулярно оси OX1. Остальные обозначения принятые на Рис.2: a - угол атаки, J - угол тангажа, q - угол наклона траектории, V - вектор воздушной скорости, Y - подъемная сила, P - сила тяги двигателей, Q - сила лобового сопротивления, G - сила тяжести, d - угол отклонения рулей высоты, Mz - момент тангажа. Продольным называется такое движение, когда вектор скорости V лежит в плоскости симметрии самолета. Используя законы механики для движения тела в подвижной системе координат и получим:
|
|
|
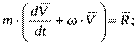
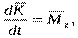где m – масса самолета, R – равнодействующая всех сил, w –угловая скорость вращения осей, K – момент количества движения, t –время. После записи уравнений в проекциях на оси полусвязанной системы координат получим:
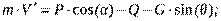
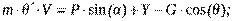
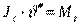где Jz – момент инерции самолета относительно оси OZ. Полученные уравнения полностью описывают продольное движение самолета. При оценке качества управляемости самолета большое значение имеет нормальная перегрузка, проекция которой на вертикальную ось OY1 полусвязанной системы координат равна:
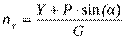
Переходные процессы по перегрузке и угловой скорости тангажа определяют оценку качества управляемости продольного движения самолета летчиком.
|
|
|
