Способы формирования выборочных совокупностей

Нерайонированный и районированный отбор. Строго случайный отбор единиц из генеральной совокупности предполагает нерайонированный и повторный отбор, т.е. отбор из всей генеральной совокупности, не разделенный на части, и при этом численность генеральной совокупности все время остается неизменной. Однако практика формирования выборочных совокупностей вносит известные улучшения в применение принципа случайного отбора, и эти улучшения повышают репрезентативность выборки и уменьшают ее ошибку при той же численности выборки.

Первое улучшение связано с тем, что применяется бесповторная выборка, дающая, как мы видели выше, меньшую ошибку.

Второе улучшение вызвано тем, что применяется районированный отбор, когда единицы в выборочную совокупность выбираются из отдельных частей (групп) генеральной совокупности, на которые она предварительно разбивается.

Если разделение совокупности осуществляется по признакам, влияющим на вариацию изучаемых показателей (выделяют типы), то такой отбор называется типическим. Даже в случае, если он не является типическим, то это облегчает формирование выборочных совокупностей и дает организационные преимущества. Кроме того, он обеспечивает более равномерное представительство всех ее частей, в результате повышается репрезентативность выборки. А типический отбор, уменьшая вариацию изучаемых признаков, снижает тем самым ошибку выборки.

Собственно-случайный отбор. Собственно-случайный отбор дает лотерея или жеребьевка, что обеспечивает абсолютно равную возможность отбора любой единицы всей совокупности. В тиражах выигрышей применяется бесповторный собственно-случайный отбор.

Механический отбор. На практике собственно-случайный отбор применить бывает сложно, и поэтому его используют редко. Обычно применяют районированный механический отбор выборочной совокупности.

При механическом отборе генеральную совокупность разбивают на интервалы, затем случайным образом выбирают единицу в первом интервале, а затем ее же выбирают во всех остальных интервалах.

Принцип случайного отбора обеспечивается в механической выборке тем, что единицы в генеральной совокупности располагаются в таком порядке, который не оказывает никакого влияния на поведение интересующего нас признака.

Типический отбор с механической выборкой. В отличие от простого механического отбора при типическом отборе группировка единиц генеральной совокупности производится не по нейтральному признаку, а по признаку, существенно влияющему на изучаемые показатели. Типический отбор выгодно применять при большой дисперсии групповых средних, когда велика межгрупповая вариация

Разновидностью типической выборки является систематический отбор – механический отбор из совокупности, ранжированной по какому-либо признаку, тесно связанному с изучаемым признаком. Например, ранжирование рабочих на заводе по среднемесячной заработной плате с целью последующего отбора для изучения семейных бюджетов рабочих.

Далее применяется - многоступенчатая выборка, многофазная выборка, комбинированное выборочное наблюдение со сплошным, малая выборка и серийная выборка

Моментные наблюдения. Суть таких наблюдений заключается в том, что на определенные моменты времени фиксируется наличие отдельных элементов изучаемого процесса.

Такие наблюдения применяют для изучения использования рабочего времени и времени работы оборудования. По охвату единиц наблюдения оно может быть сплошным, по охвату определенных периодов времени оно является выборочным.

Проверка типичности выборочных данных. Кроме вероятностной оценки репрезентативности выборочных данных путем расчета средней и предельной ошибки выборки по каждому показателю, проверка типичности выборочных данных нередко осуществляется путем сравнения выборочных характеристик со сплошными данными.

Например, типичность отобранных предприятий для формирования сети выборочных обследований рабочих проверяется путем сравнения их со всеми предприятиями по показателю средней заработной платы. По этому же критерию определяется типичность отобранных рабочих в пределах предприятий.

Существует два способа распространения данных выборочных наблюдений на генеральную совокупность: способ прямого пересчета и способ коэффициентов [ kgl]

[g1]Тема 8. Ряды динамики[:]

Цель занятия: Выявить понятие, сущность, цели и задачи динамических рядов.

Структура лекции: При изучении данной темы необходимо обратить особое внимание на вычисление средней хронологической взвешенной моментного ряда, среднего темпа роста и прироста с использованием рядов, по которым вычислялись показатели динамики

Рядами динамики в статистике называются ряды последовательно расположенных в хронологическом порядке показателей, которые характеризуют развитие явления.

В ряду динамики для каждого отрезка времени приводятся два показателя: показатель времени t и уровень ряда y.

Согласно виду приводимых в рядах динамики обобщающих показателей, их можно разделить на ряды динамики абсолютных, относительных и средних величин.

В зависимости от того, характеризуются ли уровни развития общественных явлений на определенные моменты времени или за определенные периоды времени ряды динамики принимают вид либо моментных, либо интервальных рядов динамики.

Например, данные о численности населения, численности занятых в экономике или безработных, наличии товарных запасов, площади посева зерновых могут быть представлены по состоянию на определенную дату. Они же могут быть представлены как средние или абсолютные показатели за определенный период, например, год.

Следует иметь в виду, что состояние явления учитывается моментно, его изменение – за период.

На основе рядов динамики абсолютных величин могут быть получены ряды динамики относительных и средних величин.

Важнейшими разновидностями рядов динамики относительных величин являются ряды темпов роста (например, производства продукции), изменения структуры (например, доходов и расходов республиканского бюджета) и изменения показателей интенсивности (например, выработки продукции на душу населения, численности скота на 100 га земельных угодий). На пример, к рядам средних величин относятся данные об урожайности сельскохозяйственных культур, средней выработке на одного работающего.

 

Аналитические показатели рядов динамики и приемы анализа

Рядов динамики.

Различают начальный уровень ряда y ₁, показывающий величину первого члена ряда, конечный уровень y_n, показывающий величину последнего члена ряда, и средний уровень ряда y. Методы расчета среднего уровня интервального и моментного рядов динамики различны.

В интервальном ряду, если все интервалы равны между собой, средний уровень ряда исчисляется по формуле простой средней арифметической:

 

`y = (Sy) / n,

 

где Sy – сумма уровней ряда;

n – их число.

Если интервалы в интервальном ряду разные, то средний уровень ряда исчисляется по формуле средней арифметической взвешенной:

`y = (Syf) / Sf,

 

где Sy – сумма уровней ряда;

f – число периодов, в которые преобразовываются различные интервалы ряда.

Расчет среднего уровня ряда в моментном ряду динамики осуществляется по формуле средней хронологической:

` y= (1/2 y₁ + y₂ + … + y_n-1 + 1/2 y_n) / (n – 1),

 

где n – число уровней ряда динамики.

Формула получается в результате вычисления средних уровней за период между отдельными моментами как полсуммы уровней по состоянию на начало и конец периода.

 

Показатели динамики. Для анализа динамики исчисляют следующие показатели в статистических рядах динамики: темпы роста Ty, абсолютные приросты Dy, относительные темпы прироста TDy (иначе называемого темпами прироста) и абсолютная величина одного процента прироста.

Темпами роста Ty называются отношения уровней ряда одного периода к другому. Они могут быть исчислены как базисные, когда все уровни ряда относятся к уровню одного какого-либо периода, принятого за базу. Они могут быть исчислены как цепныетемпы, когда уровни каждого периода соотносятся с уровнями предыдущего периода.

Базисные и цепные темпы роста могут быть исчислены как коэффициенты, если основания отношения принимаются за единицу, и как проценты, если основания отношения принимаются за 100. При этом обычно принято рассчитывать коэффициенты с точностью до трех знаков после запятой, а проценты – до одного знака:

 

Ty_i = y_i / y_i-1; Ty_i,баз. = y_i / y_{баз .}

или

Ty_i = y_i / y_i-1 ´100; Ty_i,баз. = y_i / y_{баз .} ´100,

 

где y_i, y_i-1 – соответственно i-й и (i –1)-й уровень;

y_{баз .} – уровень, принятый за базисный.

Если темпы выражены в коэффициентах, то легко перейти от цепных темпов к базисным и обратно, пользуясь следующими правилами:

1) произведение цепных темпов равно базисному;

2) частное от деления двух базисных темпов равно цепному.

 

Абсолютный прирост D y исчисляется как разность уровней ряда и выражается в единицах измерения показателей ряда. Его исчисляют как за отдельные периоды времени (цепной способ расчета), так и за все периоды времени с начала ряда (базисный способ расчета):

 

Dy_i = y_i - y_i-1; Dy_i,баз. = y_i - y_баз.

 

Если необходимо вычислить средний абсолютный прирост за интервал, то накопленный (базисный) прирост нужно разделить на число интервалов.

Темп прироста T D y исчисляют путем деления абсолютного прироста на величину первоначального уровня (коэффициенты) и умножения на 100 (проценты):

T D y_i = D y_i / y_i-1; T D y_{i,баз .} = D y_i / y_{баз .}

или

T D y_i = D y_i / y_i-1 ´ 100; T D y_{i,баз .} = D y_i / y_{баз .} ´ 100.

 

Он может быть также исчислен из темпов роста путем вычитания единицы или числа 100:

 

T D y_i = Ty_i – 1; T D y_i,баз. = Ty_{i,баз .} – 1;

или

T D y_i = Ty_i – 100; T D y_i,баз. = Ty_{i,баз .} – 100.

 

Показатель абсолютного значения 1% прироста равен частному от деления абсолютного прироста на темп прироста. А так как темп прироста равен частному от деления абсолютного прироста, умноженного на 100, на величину первоначального уровня, то абсолютное значение 1% прироста оказывается равным первоначальному уровню, деленному на 100. Для базисных темпов прироста этот показатель для всех лет одинаковый, для цепных – меняется:

 

Абс.зн. 1% прироста_i = D y_i / T D y_i = D y_i / (D y_i / y_i-1 ´ 100) = y_i-1 / 100;

Абс.зн. 1% прироста_баз. = D y_i / T D y_{i,баз .} = D y _i / (D y_i / y_{баз .} ´ 100) = y_{баз .} / 100.

 

Сравнительный анализ рядов динамики одноименных величин. В этом случае имеется возможность сравнивать не только темпы динамики, но и их абсолютные величины. Например, можно сравнивать динамику производства отдельных видов продукции в различных странах путем соотнесения их между собой. Так, если в 2007 г. в Казахстане было добыто 59,4 млн тонн нефти (включая газовый конденсат), то в Азербайджане 15,5 млн тонн или в 3,8 раза меньше. В то же время объем добычи нефти в Казахстане составил всего 12,9% к уровню ее добычи в России (459 млн тонн). Темп роста добычи нефти, включая газовый конденсат, в Казахстане составил 115%, в Азербайджане – 101%, в России – 109%.

При сравнении отдельных абсолютных показателей следует иметь в виду, что страны могут значительно различаться по численности населения или другим показателям, характеризующим величину («вес») страны. Так, численность населения Азербайджана почти в два раза меньше Казахстана (соответственно 8,3 и 15,1 млн человек на начало 2005 г.),

а в России, наоборот, численность населения больше, чем в Казахстане на порядок (143,6 млн человек).

Интерполяция и экстраполяция. Выравнивание рядов позволяет найти недостающие члены ряда (интерполяция) или прогнозировать дальнейшее развитие явления (экстраполяция). Прогнозирование базируется на знании закономерностей развития прогнозируемых явлений, факторов, определяющих эти закономерности, и того, как эти факторы будут вести себя в прогнозируемый период. Таким образом, прогноз является сложной экономико-статистической работой, и в этой работе известную помощь могут оказать методы экстраполяции, если они правильно улавливают сложившиеся закономерности.

Используя рассчитанные нами параметры прямой, выравнивающей фактические уровни ряда динамики среднемесячной номинальной заработной платы, рассчитаем методом экстраполяции прогнозируемое значение заработной платы в 2005 г. Оно будет выше уровня 2004 г. на 3362 тенге и составит 30765 тенге.

Приемы изучения сезонных колебаний. Некоторые социально-экономические явления имеют ярко выраженную сезонность в течение года, месяца или недели. Рядам динамики показателей таких явлений присущи колебания за определенные периоды времени. Например, к сезонным колебаниям относятся – количество туристов, численность занятых в растениеводстве, потребление топлива и электроэнергии на бытовые нужды, продажа товаров, цены на овощи и фрукты.

Сезонными колебаниями называются более или менее устойчивые внутригодовые колебания в ряду динамики, обусловленные специфическими условиями производства или потребления данного товара.

Сезонные колебания характеризуются индексами сезонности (I_s), которые являются средними величин, исчисленных из процентных отношений по одноименным месяцам фактических уровней к уровням выровненным. При этом берутся данные за несколько лет (обычно не менее трех). [kgl]

 

[g1]Тема 9. Индексы [:]

Цель занятия: Раскрыть тему экономических индексов. Их применение в экономическом анализе.

Структура лекции. Принципы и методы исчисления общих индексов

Преобразование агрегатного индекса в индексы средние.

 

Определение индекса и сфера его применения. Средние, относительные величины и всякого рода коэффициенты позволяют охарактеризовать явления и процессы. Индексы также относятся к обобщающим показателям такого рода. В широком понимании слово Index означает указатель, показатель. Однако в экономической статистике оно приобретает специфическое значение.

Индексом в статистикеназывается относительная величина, характеризующая изменение во времени и в пространстве уровня изучаемого общественного явления. Другие виды относительных величин (структуры, координации, интенсивности) к индексам не относятся, потому что при их вычислении сопоставляются не одноименные показатели, а величины разноименных явлений.

С помощью индексов решается ряд экономических задач:

1) определяются средние изменения сложных, непосредственно несоизмеримых совокупностей во времени;

2) устанавливаются средние соотношения сложных явлений в пространстве;

3) оценивается средняя степень выполнения плана по совокупности в целом или по ее части;

4) определяется роль отдельных факторов в изменении сложных явлений во времени и в пространстве и, в частности, роль структурных сдвигов.

При решении первых трех задач индексы выступают соответственно как показатели динамики, сравнения и плана, а четвертой – как аналитическое средство.

 

Использование индексов для расчета показателей динамики, сравнения и плана. Решение первых трех задач связано со сравнением двух совокупностей, непосредственно не поддающихся суммированию. Такого рода совокупности встречаются довольно часто: это натурально-вещественная форма произведенной, проданной или потребленной продукции, каждая разновидность которой представляется в различных натуральных единицах измерения. Даже если единицы измерения одинаковы (например, тонна железа и тонна риса), их нельзя напрямую суммировать.

В результате приходится рассчитывать специальные индексы физического объема, индексы себестоимости, индексы цен, индексы производительности труда, индексы урожайности и т.п.

 

Индексный метод анализа факторов динамики. Система индексов. Индексный метод может быть использован для оценки роли отдельных факторов, образующих как сомножители сложное явление, в изменении этого явления. Например, измерение стоимости выпущенной продукции может быть обусловлено изменением количества произведенной продукции и изменением цен, поскольку их произведение образует стоимость. Тогда индекс стоимости будет равен произведению индекса количества на индекс цены.

Аналогичная система индексов образуется в результате того, что стоимость произведенной продукции равна производительности труда, умноженной на затраты труда, валовой сбор зерна равен урожайности, помноженной на посевную площадь и т.д.

 

Классификация индексов. Индексы классифицируются по трем признакам: 1) по характеру изучаемых объектов; 2) по степени охвата элементов совокупности; 3) по методике расчета общих индексов.

По характеру изучаемых объектов индексы разделяются на индексы объемных показателей (физического объема продукции, розничного товарооборота, потребления и т.п.) и индексы качественных показателей (цен, себестоимости производства продукции, производительности труда, урожайности и т.п.).

По степени охвата элементов совокупности индексы делят на индивидуальные (отдельных элементов совокупности), общие (характеризующие изменение совокупности в целом) и групповые (охватывающие часть элементов совокупности). Например, индексы производства отдельных видов сельскохозяйственной продукции являются индивидуальными, индекс всей валовой продукции сельского хозяйства – общим, а индексы производства продукции растениеводства и животноводства – групповыми.

В зависимости от методологии расчета общие и групповые индексы разделяются на агрегатные (суммарные) индексы и средние из индивидуальных индексов (полученные в результате преобразования агрегатных индексов).

Рассматривая последовательный ряд индексов, исчисляемый в динамике от года к году (от месяца к месяцу, от квартала к кварталу), следует различать цепную и базисную системы расчета индексов. Индексы, рассчитываемые по отношению к одной и той же базе, называются базисными. Если же база сравнения все время меняется (когда отчетный период сравнивается с предшествующим), то индексы называются цепными.

Индексы - обобщающие показатели сравнения во времени и в пространстве не только однотипных (одноименных) явлений, а также совокупностей, состоящих из несоизмеримых элементов (цена, тонны). Индекс одноименных явлений определяются по формуле

Jq = , где «0»-это база, «1» - отчет или сравниваемый период.

Индекс Пааше: Iq = 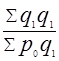- индекс постоянного состава.

 

Формула Лайсперса: Ip = - индекс постоянного состава.

Индекс выручки: Ipq = -индекс переменного состава.

 

Рассмотрим основные индексы.

• Индекс товарооборота зависит от изменения цены и от изменения физического объема товарооборота. Эта связь выражается формулой:

Ipq=It Iq

• Индекс издержек производства равен произведению индекса себестоимости на индекс физического объема:

Itq=It lq

 

Необходимость в применении индексов переменного и постоянного состава возникает в том случае, когда динамические уровни общественных явлений выражаются средними величинами.

Индекс постоянного состава определяется по обычной агрегатной форме индекса и показывает влияние только одного фактора - самой индексируемой величины. Общая формула для всех индексов имеет вид:

 

Ix =

Индекс переменного состава определяется как отношение двух средних арифметических взвешенных с переменными весами. Его изменение зависит от изменения самой индексируемой величины и от влияния структурных сдвигов.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: