Заявленная доходность бескупонных облигаций.

Т Е О Р И Я

Заявленная доходность - широко используемый показатель оценки, учитывающий как %, так и повышение курса. Есть много способов оценки заявленной доходности. Приведем метод расчета приблизительной заяв­ленной доходности,

АЗ.Д.О.=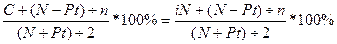

где С - годовой % доход,

i - годовой % по облигации,

N - номинал,

Pt- текущая стоимость облигации,

n- число лет, оставшихся до погашения облигации.

Задача №19

Пусть N= 1000 руб., i=10%, Pt= 800 руб. n= 10 лет. Какова будет заявленная доходность?

Решение:

АЗ.Д.О.= *100%=13,3%.

РЕАЛИЗОВАННАЯ ДОХОДНОСТЬ БЕСКУПОННОЙ ОБЛИГАЦИИ

Т е о р и я.

Если инвестор осуществляет операцию с облигацией задолго до ее погашения, то его интересует реализованная доходность. Это норма прибыли, полученная инвестором за период времени, меньший, чем срок действия выпуска.

АР.Д.О.=

где Рt+1 -ожидаемый рыночный курс,

Pt - текущий рыночный курс,

n - годы владения.

Задача №20

Пусть i= 10%, N=1000 руб., Pt= 800 руб., Рt+1 =950 руб. n1 =3 года.

 

 

Решение:

AР.Д.О.=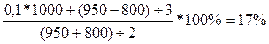

 

3. РАЗНЫЕ ЗАДАЧИ.

Задача № 21

Если число владельцев выпущенных ценных бумаг превысит 500, то согласно Федеральному закону РФ "Орынке ценных бумаг" кто должен вести список владельцев эмиссионных ценных бумаг.

1. Депозитарий,

2. Сам эмитент,

3. Уполномоченный представитель ЦБ РФ,

4. Независимая специализированная организация (держатель реестра), являющаяся профессиональным участником рынка ценных бумаг.

Ответ: Независимая специализированная организация (см.п.4), т.к. сам эмитент может вести реестр только до 500 акционеров.

Задача №22

Ценные бумаги выпускаются в одной из форм:

1. Ценные бумагина предъявителя бездокументарной Формы.

2. Ценные бумаги на предъявителя документарной формы.

3. Именные ценные бумаги документарной Формы.

4. Именные ценные бумаги бездокументарной формы.

Вопрос: Укажите, в какой форме.

Ответ: Позиции 2, 3, 4, т.к. согласно 'ФЗ РФ "О рынке ценных бумаг" ценные бумаги на. предъявителя не могут быть в бездокументарной форме. Бездокументарная Форма предусматривает запись вла­дельца ценной бумаги только в реестре (в списке владельцев эмис­сионных ценных бумаг). Бездокументарная форма ценной бумаги не в Форме документа, а в форме записи владельца в реестре.

Задача № 23

Могут ли документарные ценные бумаги быть представлены в Форме сертификатов? (Да или нет)

Ответ: Да, т.к. сертификат эмиссионной ценной бумаги - это документ, выпускаемый эмитентом, удостоверяющий право на собствен­ность указанного в нем количества ценных бумаг.

Задача № 24

Эмитент внес в проспект эмиссии недостоверные сведения. Яв­ляется ли это основанием для отказа в регистрации выпуска (Да или нет).

Ответ: Да.

Задача №25

Если выпуск ценных бумаг признан недействительным, должен ли эмитент вернуть владельцам их денежные средства? (Да или нет).

Ответ: Да, в обмен на возвращенные ценные бумаги.

 

Д Е П О З И Т Ы.

Д е п о з и т н ы е с е р т и ф и к а т ы.

Доход по депозитному сертификату определяется как D=N 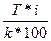, где

N-номинал сертификата,

T-количество дней (лет) на которое действует сертификат,

k – число дней в году (лет).

Задача № 26.

Организация на вторичном рынке купила депозитный сертификат с номиналом N=200000 руб., годовым % I =10% по цене S1 =198000 руб. Какова прибыль в конце второго года, т. е.Т=2 года, а k=1год.

Ответ:

 

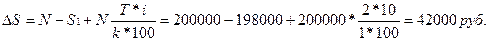
СБЕРЕГАТЕЛЬНЫЕ СЕРТИФИКАТЫ.

Задача № 27

Вы хотите через год иметь 100 000 руб., причем получить их со сберегательного сертификата в банке. Банк по вкладу обеспечивает 9% годовых.

Вопрос:

Какова приведенная стоимость будущих 100 000 руб., т. е. сколько надо сейчас положить в банк денег X на сберегательный сертификат?

Решение: X(1+0.09)=100 000 руб.

X= 100 000 1,09=91 747,12 руб.

 

ВЕКСЕЛЬ.

Задача № 28

Первое лицо должно второму лицу 500 тыс. руб., а другое лицо должно первому лицу 700 тыс. руб. У первого лица нет денег для того, чтобы расплатиться по договору со вторым лицом немедленно. А третье лицо по обязательствам должно расплатиться с первым лицом через 2 месяца. Представьте примерную схему использования переводного векселя, предусмотрев дополнительную оплату второму лицу за отсрочку платежа.

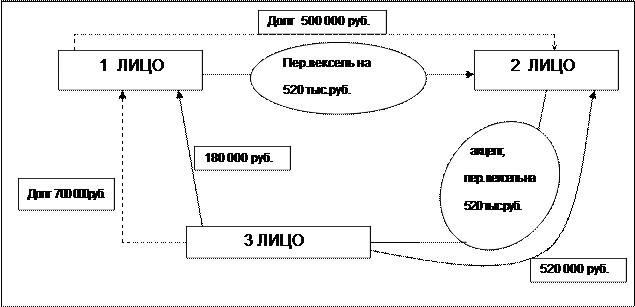Ответ по задаче 28.

 

 

В А Р Р А Н Т Ы.

 

Т Е О Р И Я.

Стоимость варранта, обеспечивающую покупку обыкновенных акций, можно определить по формуле C=(Pt-E)*n,

где Рt- текущий курс обыкновенной акции;

Е - курс исполнения варранта, т.е. курс акции, указанный в варранте, по которому инвестор ее может купить;

n- число акций, которые могут быть куплены на один варрант.

Если n= I, то С = Рt - Е.

Пример: Если Рt= 500 руб., а Е=400 руб., то С = 100 руб. - стоимость варранта.

Т.е. если держатель варранта не захочет покупать акции, он может в принципе продать варрант по цене до 100 руб. Цена равная 100 руб. может быть в том случае, когда новый покупатель варранта другим способом не может приобрести акции.

Задача № 29.

ОАО «Салют» выпустило серию из 100 варрантов, каждый из которых дает владельцу варранта право приобрести пакет из 100 акций (стандартный лот) по цене 1000 руб. за штуку. Но на рынке ценных бумаг цена акции поднялась, и она стала стоить 1300 руб.

Вопросы.

1. Какова стоимость одного варранта, если владелец захочет его продать?

Ответ: Св = (1300 - 1000) * 100 = 30 000 руб.

3. Какова стоимость всех варрантов данного выпуска?

Ответ:

Задача № 30.

Потенциальный акционер приобрел варрант, который дает право приобрести стандартный лот акций по цене каждой акции 1000 руб. Однако на рынке цена акций поднялась и акция стала стоить 1300 руб. Стоимость варранта в этом случае стала

Св = (1300 – 1000) * 100 = 30 000 руб.

Вопросы.

1. При каких условиях владелец варранта продаст его по цене ниже 30 000 руб., например, 25 000 руб.?

Ответ: Очевидно, при любых, т. к. продавец варранта в этом случае заработает 25 000 руб., а покупатель варранта приобретает пакет из 100 акций по цене 1000 *100 + 25 000 = 125 000 руб.. Тогда как на рынке ценных бумаг он эти же 100 акций приобрел бы по цене 1300 * 100 = 130 000 руб.

2. При каких условиях владелец варранты может продать его по цене 30 000 руб.?

Ответ: Очевидно, это будет сделать не просто, т. к. покупатель и так просто может приобрести лот за 130 000 руб., и ему незачем покупать этот варрант. Но покупатель может купить все – таки варрант, если количество продаваемых акций на рынке ограничено, а срок действия варранта еще не истек.

3. В каких случаях владелец варранта может его продать по цене выше 30 000 руб.?

Ответ: Теоретически это можно сделать в том случае, если срок действия варранта еще не истек, а цены на эти акции продолжают интенсивно расти. В этом случае покупатель может купить варрант по цене, большей 30 000 руб. в надежде получить в будущем прибыль от роста курса акций. Хотя он рискует в определенной степени.

Задача № 31.

Инвестор купил 40 варрантов на обыкновенные акции известной нефтяной компании из расчета 20 руб. за акцию. Один варрант даёт право на приобретение одного лота (100 шт.) акций по цене 1000 руб. за акцию. Но на вторичном рынке акции этой нефтяной компании подорожали до1200 руб.

Вопрос:

Какова может быть прибыль, если инвестор реализует свое право на получение 40 варрантов, а затем продаёт весь пакет акций на вторичном рынке.

Ответ: С учетом стоимости варранта инвестору весь пакет акций будет стоить 40 вар * 100 акц. (1000 + 20) = 4 080 000 руб. Возможная прибыль составит 4 800 000 – 4 080 000 = 720 000 руб.

Задача № 32.

Инвестор приобрел пакет варрантов на обыкновенные акции по цене из расчета 20 руб. за акцию. Варрант даёт право приобретать акции по цене 1000 руб. Но на вторичном рынке цена акций пока составляет 980 руб.

Вопрос.

На сколько должна повыситься цена акции, чтобы инвестор мог купленные по варранту акции продать и окупить свои затраты?

Ответ: Каждая акция по варранту обойдется инвестору по цене 1000 + 20 руб. = 1020 руб. Следовательно, для компенсации затрат инвестора (без прибыли) цена акции на вторичном рынке должна вырасти на 40 руб. (т. е. 1020 - 980 = 40 руб.).

Задача №33

Пусть цена обыкновенной акции Рt = 500 руб., стоимость акции,

указанная в варранте 400 руб. Пусть для простоты n=1. Цена акции повысилась на 100 руб. и стала 600 руб.

Вопрос: Определить новую стоимость варранта и увеличение в %стоимости акции и варранта.

Решение: Стоимость варранта в расчете на одну акцию составит

600 - 400 руб. = 200 руб.

Стоимость акции увеличилась на(100/500)*100%=20%.

Стоимость варранта за это же время изменилась на (100/100). 100% = 100%.

Таким образом, норма прибыли варранта в 5 раз больше, чем норма прибыли обыкновенной акции. Следовательно, операции с вар­рантами могут приносить хороший доход.

 

С Т Р И П Ы.

Т е о р и я.

Стрип - это ценная бумага, которая представляет собой бескупонную облигацию и погашается за счет процентных выплат по пакету государственных облигаций, принадлежащих организации, выпустившей эти облигации страны.

Задача № 34.

Компания «Х» владеет пакетом государственных облигаций совокупной номинальной стоимостью 4 000 000 руб. Государственные облигации – купонные, проценты по ним выплачиваются 1 раз в год, размер купонного процента – 10 %. Компании потребовались срочно деньги и она размещает серию стрипов сроком на 3 года. Номинал одного стрипа - 50 000 руб.

Вопрос.

Сколько стрипов может выпустить компания?

Ответ: Определяем общий объем процентных выплат по государственным облигациям за 3 года 4 000 000 х 0,1 х 3 = 1 200 000 руб.

Количество стрипов составит 1 200 000: 50 000 = 24 стрипа.

Задача № 35.

Компания «Х» владеет муниципальными облигациями на сумму 20 000 000 руб. Проценты по этим бумагам выплачиваются 2 раза в год. Проценты по купону – 5 %. Компании срочно понадобились деньги, и она решила выпустить стрипы в количестве 1000 штук, сроком на 2 года.

Вопрос.

По какой цене покупатель (инвестор) стрипа должен его купить, чтобы потенциальный доход по нему равнялся 500 руб.?

Ответ:

1.Определим размер процентных выплат по облигациям за 2 года

20 000 000 * (0,05 + 0, 05) * 2 года = 4 000 000 руб.

2.Определим стоимость одного стрипа

4 000 000 / 1000 = 4000 руб.

3.Определим цену покупки, чтобы обеспечить покупателю стрипа необходимый доход 4000 – 500 = 3500 руб.

Задача № 36.

Организация «Х» владеет крупным пакетом государственных облигаций на сумму 25 000 000 руб. По облигациям выплачиваются купонные проценты в размере 10 % от номинала. Руководство компании «Х», исходя из своих соображений, решило выпустить стрипы номиналом 30 000 руб., но не на всю сумму своих облигаций, а на 10 000 000 руб. Срок обращения стрипов установлен в 3 года.

Вопросы.

1. Сколько стрипов можно в этом случае выпустить?

2. Какую прибыль может получить покупатель 10 стрипов в момент даты погошения, если он приобрел стрипы по цене 27 000 руб.?

Ответы:

1. Какова стоимость стрипов: 10 000 000х0,1 х 3 года =3 000 000 руб.

2. Каково количество стрипов?

3 000 000 / 30 000 = 100 шт.

3. Какова номинальная стоимость 10 стрипов?

30 000 * 10 = 300 000 руб.

4. Какую сумму заплатил покупатель 10 стрипов?

27 000 * 10 = 270 000 руб.

5. Каков может быть его доход в момент погашения стрипов?

300 000 – 270 000 = 30 000 руб.

Вывод:

Как видим, стрипы тоже могут котироваться. Стрип – это бескупонная облигация, и если их владелец будет держать их у себя до погашения, то заработает 30 000 руб.

 

РАЗНЫЕ ЗАДАИ

Задача № 37.

Указать, какие цели может преследовать инвестор, покупая обыкновенные акции:

1. Получение дохода.

2. Уход от налогов.

3. Размещение свободных денежных средств.

4. Планирование будущих поступлений в свой бюджет.

5. Участие в управлении эмитента.

6. Повышение имиджа своей фирмы.

Ответ: 1, 3, 5.

Задача № 38.

То же при покупке привилегированных акций.

Ответ: 1. 3, 4.

 

 

Задача № 39.

За счет чего основной доход по акции получает инвестор?

1. Роста курсовой стоимости акции.

2. Получения дивидендов.

3. Участия в управлении компанией – эмитентом.

4. Облегчения налогового бремени.

Ответ: 1, 2.

Задача № 40.

Имеет ли облигация фиксированное время погашения?

1. Да. 2. Нет.

Ответ: Да.

Т е о р и я.

Доходность ценной бумаги определяется в % годового дохода.

Д ц. б. = ,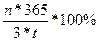

где Д -- доходность в %,

n -прибыль от операции с ценной бумагой,

З - затраты на покупку ценной бумаги,

Т - время владения ценной бумагой, 365 – количество дней в году.

Убыточность ценной бумаги определяется также в % годовых.

Уцб =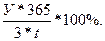

Задача № 41.

Бескупонная облигация с номиналом 1000 руб. куплена за 900 руб. 1 февраля, а дата погашения - 31 декабря.

Вопрос:

Определить доходность облигации в % годовых.

Ответ: Т. к. облигация бескупонная, доход от неё будет равняться разности между номиналом и ценой покупки:

n = 1000 – 900 = 100 руб.

Доходность в % годовых составит

Д ц.б.= 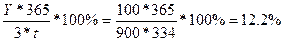годовых

где 334 дня - период, в который покупатель держит облигации у себя.

Задача 42.

Серия вопросов:

1. Может ли слух повлиять на курс той или иной ценной бумаги? Да или нет? Ответ: Да.

2. Раскачивают ли спекулянты вторичный рынок ценных бумаг? Да или нет? Ответ: Да.

3. Кто такие медведи и быкина вторичном рынке ценных бумаг?

Ответ:

4. У кого больше шансов успешно работать на вторичном рынке ценных бумаг?

а) У неопытного игрока,

б) У опытного игрока.

Ответ: б).

Задача 43.

Определить, какой вариант вложения денежных средств выгоднее?

1. Вложить деньги на срок с I апреля до I октября в банк на депозит под 10% годовых (т.е. на 6 месяцев).

2. Купить I апреля пакет бескупонных облигаций по цене 1890 руб. с

номиналом 2000 руб. и датой погашения I октября.

Ответ:

Доходность по варианту I известна – 10% годовых. Подсчитаем доходность по второму варианту:

Дц.б.=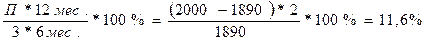

Следовательно, вариант №2 более выгоден.

Задача № 44.

 

Задача предназначена для общего разбора в аудитории, она целиком заимствована из книги Царихина К.С. «Рынок ценных бумаг, М., 2003^».

Условие: У нас есть I 000 000 руб. Требуется определить, какой вариант вложения денег более выгоден.

Вариант I

 

Купить I марта 2008г. пакет бескупонных облигаций по цене 480 руб. за штуку, номиналом 500 руб. и датой погашения I сентября 2008г. Затем вырученные деньги реинвестировать в купонные облигации номина­лом 1000 руб. и сроком погашения I марта 2009г., купив их по 990руб., учитывая при этом, что эмитент выплатит I декабря 2008г. купонный про­цент в размере 2% от номинала.

Вариант 2

 

Купить I марта 2008г. пакет купонных облигаций по 1010 руб. с номиналом 1000 руб., датой погашения I декабря 2008г. и следующими купонными выплатами: I июня 2008г. - 2% от номинала, 2 сентября 2008 г, - 2% от номинала и I декабря 2008г. - 20 руб. Затем вырученные деньги реинвестировать а пакет бескупонных облигаций, купив их по цене 290 руб.за штуку (номинал 300 руб.), а дата погашения I марта 2009г.

Вариант 3

Положить деньги в банк под 9% годовых.

Замечание:

Для упрощения ситуации налоги во всех случаях не учитывать.

 

Так как известна начальная сумма денег, то можно просто подс­читать прибыль по первому и второму вариантам, а потом сравнитьих(в приведенном решении некоторые промежуточные величины округлены).

Вариант I

 

1. На I 000 000 руб. мы купим 1,03.2006г. I 000 000/ 480 = 2083 обли­гации.

2.1.09.2006 г. мы получим за них 2083 * 500 = I 041 500 руб.

3.На эти деньги получаем I 041 500/ 990 в 1052 купонных облигаций,

4. При погашении получаем заних I 052 000 руб. + купонные выплаты

1052 * 1000 * 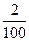=21 040 руб.

5. Прибыль составит I 073 040 - I 000 000 = 73 040 руб.

 

Вариант 2

1. На I 000 000 руб. покупаем 1.03.2006г. I 000 000 / 1010 = 990 купонных облигаций.

2. При погашении их I декабря 2009г. мы получаем

990 * 1000 =990 000 руб. плюс купонные выплаты

990 * 1000 *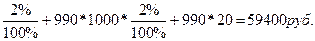

Итого мы получаем

990 000 + 59 400 = 1 049 400 руб.

3, На эти деньги мы покупаем I 049 400 / 290 = 3619 бескупонных облигаций.

4. При погашении бескупонных облигаций 1.03,2007г. получаем

3619 * 300 =I 085 700 руб.

5. Итоговая прибыль составляет I 085 700 - I 000 000 = 85 700 руб.

Следовательно: 2-й вариант более выгоден.

Вариант 3

Если I 000 000 руб. положить в банк под 9% годовых, то прибыль составит 90 000 руб. Следовательно, это самый выгодный вариант. К тому же по банковскому депозиту нет налогов.

Задача № 45.

Какой вариант вложения денежных средств более эффективен:

Вариант I

I марта 2008г. мы покупаем пакет бескупонных облигаций по 950 руб., а I сентября 2008г. их погашают по номинальной цене 1000 руб. Затем мы покупаем пакет купонных облигаций по 980 руб. с датой по­гашения I марта 2009г. номиналом 1000 руб. и двумя купонными выпла­тами по 2% от номинала. Таким образом, операция заканчивается I марта 2009г.

Вариант 2

 

I марта 2008г. мы покупаем пакет купонных облигаций по 510руб. с номиналом 500 руб., датой погашения I декабря 2008г. и тремя ку­понными выплатами по 3% от номинала. После этого мы вкладываем по­лученные деньги на депозитный сертификат под 10% годовых сроком до I марта. Так как по условию задачи начальная сумма неизвестна, и мы реинвестируем денежные средства, то нам необходимо найтине абсолютное значение прибыли, а относительную величину прибыли (ОВП), равную Дцп.

Вариант I

Пусть у нас первоначально было Х руб. Тогда

Дцп =

Следовательно, I сентября у нас будет Х * 1,0502руб.

Далее определяем (ОВП) =за второй период.

Дцп =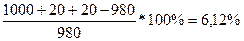

Тогда к I марта 2009г. по первому варианту у нас будет

(X. 1,0502). 1,0612 = Х. 1,116

Таким образом, наша первоначальная сумма увеличитсяна 11,16%.

 

Вариант 2

Первоначально у нас также Х руб,

Дцп =

Тогда к I декабря кладем деньгина депозит. Прибыльза I ква­ртал составит

10/ 4 = 2,5%.

Итого к 1 марта 2009г. по второму варианту будет

(X,1,0686). 1,0025 = X.1,095, т.е. наша первоначальная сумма

увеличилась на 9,5%.Следовательно, первый вариант выгоднее.

 

 

Задача № 46.

Акционерное общество выпустило 9000 обыкновенных акций, 1000 привилегированных акций и 1500 облигаций. Номинал всех ценных бумаг 1000 руб. Процент по облигациям составляет 11%, дивиденд по привилегированным акциям – 15%.

Вопрос: Каким образом между собой будут соотносится доходы держателей различных ценных бумаг, если прибыль к распределению между акционерами составила 1600000 руб.

Решение:

Замечание. Сначала дадим разъяснение. Проценты по облигациям (процентным), т.е. долговым бумагам, должны выплачиваться независимо от результатов хозяйственной деятельности. Причем согласно налоговому кодексу проценты по долгам платятся из прибыли до налогообложения в размере 1,1 ставки рефинансирования, а то что сверху – из собственных средств, т.е. из чистой прибыли.

При ставке рефинансирования 10% условие выполняется.

По решению собрания акционеров решено из чистой прибыли направить на выплаты по акциям 1 600 000 руб.

Рассмотрим размер выплат в качестве дивидендов по привилегированным акциям: 0,15 × 1000 × 1000 = 150 000 руб.

Тогда оставшаяся сумма для выплат дивидендов по обыкновенным акциям составит: 1 600 000 – 150 000 = 1 450 000 руб.

Вычислим размер выплат дивидендов по одной обыкновенной акции:

1 450 000: 9 000 = 161 руб.

Итак, выплаты составляют:

- по облигациям – 100 руб/шт.

- по привилегированным акциям – 150 руб/шт.

- по обыкновенным акциям – 161 руб/шт

Замечание. Если бы прибыли не было вовсе, то выплаты по обыкновенным акциям не производились бы. А выплаты по облигациям и по привилегированным акциям все равно имели бы место из собственных средств или из резервного фонда акционерного общества.

Задача №47

Определить целесообразность покупки облигации, если текущий рыночный ее курс Р = 920 долларов, срок погашения – 5 лет, ставка годового купона – 7%, номинальная стоимость N = 1000 долларов.

Доходность к погашению для данной облигации У определяется из уравнения:

V = C1/(1+У)1 + C2/(1+У)2 + C3/(1+У)3 + C4/(1+У)4 + C5/(1+У)5

или

n

Р = ∑ Ci/(1+У)i

i=1

 

Решение.

Очевидно, что ежегодные выплаты по купонам в последующие 4 года равны:

С1 = С2 = С3 = С4 = С = 70 долларов., т.е. С1,2,3,4 = i

N = 0,07 * 1000 = 70 долларов.

А в 5-й год выплата по облигации будет:

N + C = 1000 + 70 = 1070 долларов.

Тогда подставив эти данные в исходное уравнение получим:

920 = 70/(1+У)1 + 70/(1+У)2 + 70/(1+У)3 + 70/(1+У)4 + 70/(1+У)5

Из уравнения можно получить У = 0,0906 = 9,06%

Если последующий анализ показывает что процентная ставка (У*) с учетом роста курсовой стоимости может быть равна У* = 8,00%, то данная облигация недооценена, так как У > У*, следовательно, она может быть рекомендована для покупки в данной момент времени.

Может быть другое решение данной задачи в рамках метода капитализации дохода.

Внутренняя стоимость ценной бумаги (облигации) V может быть вычислена по следующей формуле:

 

V = C1/(1+У*)1 + C2/(1+У*)2 + C3/(1+У*)3 + C4/(1+У*)4 + C5/(1+У*)5

или

n

V = ∑ Ci/(1+У*)i

i=1

 

Поскольку цена покупки облигации – это ее рыночный курс, то для инвестора чистая приведенная стоимость NPV равна разности между внутренней стоимостью облигации и ценой покупки:

n

NPV = V – P = ∑ Ci/(1+У*)I – P

i=1

Рассчитаем NPV для облигации из рассматриваемого примера:

NPV = (70/(1+0,08)1 + 70/(1+0,08)2 + 70/(1+0,08)3 + 70/(1+0,08)4 + 70/(1+0,08)5 – 920 = 40,15 долларов.

Поскольку показатель NPV для данной облигации положителен, это свидетельствует о том что ее теоретическая стоимость выше, чем рыночная. А это является сигналом для покупки.

Конечно при решении данной задачи необходимо определить величину У*, это не так просто, т.к. она зависит от субъективной оценки инвестора, некоторых характеристик облигации и текущих условий на рынке.

У Центрального Банка России такая методика есть, но он ее не раскрывает.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: