 |
ных посылок нельзя вывести заключения; если одна из
|
|
|
|
ных посылок нельзя вывести заключения; если одна из
посылок отрицательная, то и заключение будет отрицательным.
Возьмём пример:
Ни один электрон (М) не находится в покое (Р). Протон (S) не электрон (М).
Следует ли из этих посылок, что «протон находится в покое»? Нет, не следует. Из этих посылок вообще нель
зя вывести заключения.
Если обе посылки отрицательные — это значит, что отрицается всякая связь среднего термина с другими двумя
терминами силлогизма. Но если М не связано ни с S, ни с Р, то нет возможности установить, в каком именно отношении находятся S и Р.
Чертежи 19, 20, 21, 22 изображают положение терминов в отрицательных посылках. Термин М не связан ни с S, ни с Р, и поэтому мы не можем сказать ничего опре
делённого об отношении S и Р.
Но если из двух посылок силлогизма отрицательной будет только одна, то заключение вывести можно, причём всегда отрицательное.
Возьмём пример:
Ни одно споровое растение (М) не размножается семенами (Р). Мох (S) — споровое растение (М).

Из этих посылок вполне закономерно следует един ственно возможный вывод: «Мох не размножается семе нами».
Почему заключение всегда будет отрицательным, если одна из посылок отрицательная? В нашем примере боль шая посылка указывает на отсутствие связи между тер минами М и Р. Но S входит в состав М, следовательно, согласно аксиоме силлогизма, отрицается связь между S и Р.
Если же отрицательной была бы не большая, а меньшая посылка, то отрицалась бы связь между S и М, сле
довательно, между S и Р.
Итак, когда одна из посылок отрицательная, то и заключение отрицательное. И соответственно наоборот: отрицательное заключение может получиться только при том условии, если одна из посылок отрицательная. Из утвердительных посылок не может получиться отрицательного заключения.
|
|
|
П я т о е п р а в и л о. Из двух частных посылок
нельзя вывести заключения; если одна из посылок част
ная, то и заключение будет частным.
Это правило относится к таким частным посылкам, в которых предикат не распределён.
Обратимся к примеру:
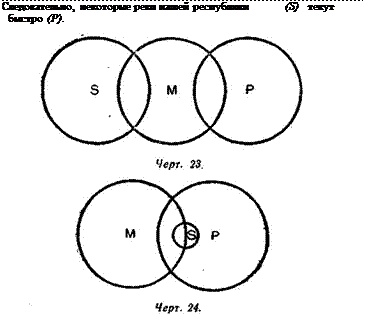
Некоторые студенты (М) — шахматисты (Р).
Некоторые рабочие нашего завода (S) — студенты (М).
Следует ли из этих посылок, что «Некоторые рабочие нашего завода — шахматисты»? Чертежи 23 и 24 показывают, что такой вывод не обязателен. Поскольку средний термин не распределён в обеих посылках, постольку
единственно возможного вывода из данных посылок получить нельзя (см. правило второе).
Если одна из посылок частная, то в заключении нельзя получить общего суждения. Это видно из следующего
примера:
Некоторые грибы (М) съедобны (Р).
Все грибы (М) — растения (S).
Так как меньший термин в посылке не распределён, то и в заключении он должен быть нераспределённым (см. правило третье). Следовательно, вывод может быть толь
ко один: «Некоторые растения съедобны».
В соответствии с правилом третьим, заключение будет частным и в том случае, если частной будет не большая, а меньшая посылка.
Например:
Все горные реки (М) текут быстро (Р).
Некоторые реки нашей республики (S) — горные (М).
Итак, когда одна из посылок частная, то и заключение частное. Однако когда обе посылки общие, то возможна частное заключение.
Например:
Вольфрам (М) имеет высокую температуру плавления (Р).
Вольфрам (М) — металл (S). 
Следовательно, некоторые металлы (S) имеют высокую температуру плавления (Р).
Вывести общее заключение из данных посылок нельзя, так как это было бы нарушением третьего правила («непозволительное расширение меньшего термина»), которое
|
|
|
выражает закон достаточного основания.
|
|
|


