Самостоятельная работа студента

РОССИЙСКАЯ АКАДЕМИЯ НАРОДНОГО ХОЗЯЙСТВА и ГОСУДАРСТВЕННОЙ СЛУЖБЫ

При ПРЕЗИДЕНТЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

(РАНХиГС)

Факультет
«Международный институт государственной службы и управления» (МИГСУ)

УТВЕРЖДЕНО

______________________ /__________/

«_____» __________ 2013 г.

 

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

Линейная алгебра

 

Автор: кандидат физико-математических наук, доцент, Поленова Т.М.

 

Направление: 080100.62«Экономика»

Профиль: «Финансовый контроль и государственный аудит»

Квалификация (степень) выпускника: БАКАЛАВР

Форма обучения: очная

 

Москва 2013 г.

МЕСТО УЧЕБНОЙ ДИСЦИПЛИНЫ В СТРУКТУРЕ ООП ВПО

 

Учебная дисциплина «Линейная алгебра» относится к естественнонаучному и математическому циклу дисциплин Б2 подготовки студентов по направлению 080100.62 «Экономика». Изучение разделов дисциплины опираются на знания, полученные студентами в общеобразовательной школе по дисциплинам «Алгебра», «Геометрия». Дисциплина «Линейная алгебра» является базовой для последующего изучения учебных дисциплин: «Математический анализ», «Теория вероятностей и математическая статистика», «Методы оптимальных решений», «Моделирование экономических процессов», «Количественные методы в экономике», «Исследование операций».

 

2. ЦЕЛИ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

 

Основной целью учебной дисциплины «Линейная алгебра» являются формирование математической культуры, основных знаний, навыков и компетенций в области математики, необходимых для изучения последующих дисциплин образовательной программы и успешного осуществления профессиональной деятельности.

ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ ОБРАЗОВАНИЯ И КОМПЕТЕНЦИИ СТУДЕНТА ПО ЗАВЕРШЕНИИ ОСВОЕНИЯ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

В результате освоения дисциплины студент должен:

- знать определения, теоремы, подходы к решению задач из основных разделов высшей математики;

- уметь применять методы линейной алгебры и моделирования экономических процессов;

- владеть навыками научного анализа экономических проблем и процессов, навыками практического использования базовых знаний и методов математики и естественных наук.

 

Должны быть сформированы следующие компетенции:

- Общекультурные:

(ОК-1) - владеет культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения.

 

- Общепрофессиональные:

(ПК-5) – способен выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы

(ПК-6) – способен на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты

 

 

СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

Организационно-методичекие данные дисциплины

Вид учебной работы	Количество часов
Всего по учебному плану	Семестры
Аудиторные занятия (всего):
В том числе:
Лекции (Л)
практические (ПЗ) и семинарские (С) занятия
лабораторные работы (ЛР) (лабораторный практикум) (ЛП)
Контроль самостоятельно работы (КСР):
Самостоятельная работа (всего):
ОБЩАЯ трудоемкость дисциплины:	Часы:
Зач. ед.:
Текущий контроль (количество и вид текущего контроля)	к/з
Виды промежуточного контроля (экзамен, зачет)	Э	Э

4.2. Тематический план дисциплины

Наименование тем	Количество часов (в акад. часах и/или кредитах)
Лекции	Практические занятия	Самостоятельн. работа	Всего часов по теме
Тема 1. Матрицы и определители.
Тема 2. Системы линейных алгебраических уравнений.
Тема 3. Линейные пространства и преобразования.
Тема 4. Комплексные числа. Собственные значения и векторы.
Тема 5. Квадратичные формы
Тема 6. Элементы аналитической геометрии
Итого по курсу:	32/0,8	32/0,8	80/2,4	144/4

Содержание тем дисциплины с указанием лабораторных и/или практических занятий при наличии

Тема 1. Матрицы и определители.

Определение и виды матриц. Векторы. Операции над матрицами. Определитель квадратной матрицы. Минор. Алгебраическое дополнение. Вычисление и свойства определителей. Элементарные преобразования строк и столбцов матрицы. Обратная матрица. Ранг матрицы.

Практическое занятие 1.

1. Повторение определений основных понятий темы.

2. Даны матрицы A и B.

а)

Указать, какие из нижеприведенных операций выполнимы, и выполнить их.

а) A + B; б) AT + B; в) A + B T; г) AT + B T.

д) AB; е) ATB; ж) AB T; з) BAT.

3. Решить задачи [Л1[1], с.60, 64]:

1.17, 1.20, 1.23; 1.40, 1.43

4. Найти определитель матрицы

Практическое занятие 2.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с.65, 68]: 1.51; 1.62

3. Найти матрицу, обратную матрице С, если она существует (см. п. 4 занятия 1).

4. Найти ранг матриц

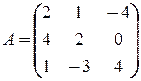
5. Решить задачи [Л1, с.70-71]: 1.71; 1.73; 1.79

Практическое занятие 3.

1. Повторение определений основных понятий темы.

2. Найти значение многочлена f(x) от матрицы А [Л1, с.61]: 1.35

3. Решить задачи с экономическим содержанием [Л1, с.72-77]:

1.88; 1.89; 1.90;1.91

Тема 2.Системы линейных алгебраических уравнений (СЛАУ). Запись и решение СЛАУ в матричном виде. Формулы Крамера. Теорема Кронекера-Капелли о разрешимости системы. Решение СЛАУ и вычисление обратной матрицы методом Гаусса. Системы линейных однородных уравнений; свойства, фундаментальное решение. Общее решение системы линейных алгебраических уравнений; свободные неизвестные, базисные решения. Модель Леонтьева - модель многоотраслевой экономики.

Практическое занятие 1.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 108]: 2.14, 2.19, 2.22

3. Решить системы уравнений методом Гаусса

а) 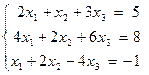; б) .

4. Решить задачу 2.46 [Л1, с. 115]:

Практическое занятие 2.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 108, 115]: 2.26, 2.47;

3. Найти базисные и общее решения системы уравнений из задач [Л1, с. 115-116]. 2.52, 2.54.

Практическое занятие 3.

1. Повторение определений основных понятий темы.

2. Решить системы уравнений, найти все базисные решения [Л1, с.116]: 2.56; 2.58

3. Найти фундаментальные системы решений систем линейных уравнений [Л1, с.116-117]: 2.60; 2.62; 2.64

4. Решить задачи[Л1, с.117-119]: 2.67; 2.69.

Тема 3. Линейные пространства и преобразования.

Векторы на плоскости и в трехмерном пространстве. Определение и примеры линейного пространства. Линейная зависимость и независимость векторов. Базис. Координаты. Размерность. Скалярное произведение. Ортонормированный базис. Евклидовы пространства. Линейные преобразования (операторы). Способы нахождения матрицы линейного преобразования.Ранг и дефект линейного преобразования.

Практическое занятие 1.

1. Повторение определений основных понятий темы.

2. Доказать, что множество двухмерных геометрических векторов с заданными на нем операциями сложения и умножения на число образует линейное пространство.

3. Решить задачи [Л1, с. 165-166]: 3.50, 3.53, 3.56, 3.58, 3.61

4. Найти косинус угла между векторами x и y, принадлежащими трехмерному евклидову пространству с ортонормированным базисом.

а) , б) , .

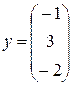5. Решить задачи [Л1, с. 158-159]:

3.20, 3.26

Практическое занятие 2.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1,с.158,с.159,с.166, с. 168-169]:

3.20, 3.26, 3.65, 3.71, 3.73, 3.78

в вектор

3. Найти матрицу линейного преобразования, переводящего каждый

вектор

 

 

Практическое занятие 3.

1. Повторение определений основных понятий темы.

2. Найти матрицу линейного преобразования, переводящего каждый вектор x двухмерного векторного пространства в вектор y по следующему алгоритму.

а) симметричное отображение относительно прямой x₁ = x₂;

б) поворот на 45° по часовой стрелке;

в) симметричное отображение относительно прямой x₁ = 0, а затем симметричное отображение относительно начала координат.

3. Решить задачи [Л1, с. 169]: 3.80; 3.82.

 

Тема 4 Комплексные числа. Собственные значения и векторы.

Определение, геометрическая интерпретация и формы записи комплексных чисел. Операции над комплексными числами и их свойства. Возведение в степень и извлечение корня из комплексного числа. Собственные значения и собственные векторы матриц, свойства собственных векторов. Линейная модель обмена.

 

Практическое занятие 1.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 805-806]:

15.7, 15.8в, 15.12, 15.22

3. Даны комплексные числа . Представить в тригонометрической форме и экспоненциальной форме и изобразить на комплексной плоскости эти числа, а также

Практическое занятие 2.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 172-173]:

3.87, 3.91. 3.96. 3.102

Тема 5. Квадратичные формы.

Понятие квадратичной формы. Матричная запись. Канонический вид квадратичной формы. Положительно и отрицательно определенные квадратичные формы. Критерий Сильвестра.

Практическое занятие 1.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 176, 177]: 3.111, 3.117, 3.120, 3.124

Практическое занятие 2.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 177]: 3.131, 3.133, 3.135

 

Тема 6. Элементы аналитической геометрии.

Уравнение линий на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой. Кривые второго порядка Уравнения плоскости и прямой в пространстве. Углы между плоскостями и прямыми. Условия параллельности и перпендикулярности. Поверхности второго порядка, их геометрические свойства. Элементы аналитической геометрии в n-мерном пространстве. Подпространства. Прямые и гиперплоскости в линейном пространстве.

Практическое занятие 1.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 217, 218]:

4.21, 4.35, 4.37, 4.38, 4.47;

 

Практическое занятие 2.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 217, 225–227, 235]:

4.69, 4.79, 4.93, 4.119

 

Практическое занятие 3.

1. Повторение определений основных понятий темы.

2. Решить задачи [Л1, с. 229–236]:

4.108, 4.114, 4.116, 4.119

 

САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТА

На самостоятельную работу студента выделяется 80 часов (раздел 4.2.). Студенту рекомендуется использовать время, отведённое на самостоятельную работу, для просмотра конспектов лекций и ознакомления с литературой по теме лекций - 20 часов, подготовки к выполнению текущих домашних заданий -30 часов, домашнего контрольного задания – 12 часов, подготовки к экзамену -18 часов.

Текущие домашние задания выполняются студентом к каждому практическому занятию.

Для выполнения этих заданий студент обязан проработать лекции по соответствующим темам, присутствовать и работать на практических занятиях, где разбираются и решаются задачи определенные в темах занятий.

Домашние контрольные задания выполняются студентами по индивидуальным вариантам, которые они получают у преподавателя ведущего практические занятия, и предоставляются к определенным срокам.По данной дисциплине предусмотрено выполнение двух домашних контрольных задания. Каждое домашнее контрольное задание состоит из 6 задач. Таблица вариантов и задачи к вариантам представлены в разделе «Задания для самостоятельной работы студентов». Сроки представления и оценка домашних контрольных заданий описана в разделе 6 данной программы.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: