 |
Критерии оценки знаний, умений, навыков
|
|
|
|
Для контроля усвоения данного курса учебным планом предусмотрен экзамен как форма аттестационного испытания. Оценка выставляется в соответствии с требованиями балльно-рейтинговой системы.
Аттестация осуществляется по результатам выполнения всех видов работ, предусмотренных программой изучения дисциплины (активность на семинарских занятиях; контрольных домашних работ; контрольных аудиторных работ), устного экзамена.
Посещение семинарских занятий учитывается при аттестации.
Описание балльной структуры оценки:
§ Максимальное количество баллов в семестре – 100.
§ Максимальное количество баллов за выполнение каждого вида работ (в семестре):
- активная работа на семинарах, домашние задания, посещаемость – 60 балла (16 баллов – работа на семинаре, 12 баллов – выполнение домашних работ; 32 балла – посещение занятий (2 балла за одно практическое занятие));
- контрольные аудиторные работы (две) – 10 баллов;
- контрольные домашние работы (две) – 10 баллов;
- экзамен (с итоговым тестированием) – 20 баллов.
Оценка неудовлетворительно выставляется, если студент набрал менее 50 баллов.
Студент не допускается к аттестации по дисциплине, если он набрал менее 35 баллов.
Если студент набрал от 36 до 49 баллов, то он может пройти повторную аттестацию по дисциплине в рамках сессии.
Студенту выставляется «неудовлетворительно» и в том случае, если он за итоговую контрольную работу набрал менее 8 баллов, независимо от количества баллов, полученных по дисциплине в течение семестра.
Оценка удовлетворительно выставляется при условии, если студент набрал от 50 до 65 баллов.
Оценка хорошо выставляется при условии, если студент набрал от 66 до 75 баллов.
|
|
|
Оценка отлично выставляется при условии, если студент набрал от 76 до 100 баллов.
100 баллов выставляется не только при условии выполнения всех требований, но и с обязательным проявлением творческого отношения к предмету, умения находить оригинальные, не содержащиеся в учебниках ответы, умения работать с источниками, которые содержатся дополнительной литературе к курсу, умения соединять знания, полученные в данном курсе со знаниями других дисциплин.
Контрольные и текущие задания по темам курса
Выполняется две контрольные работы из 6 задач. Номер варианта задания равен номеру студента в списке группы (в журнале). С помощью таблицы вариантов, приведенной в Приложении 1, определяются номера вариантов входящих в задание задач. Образец оформления титульного листа задания приведен в Приложении 2.
Контрольное задание 1
Задача 1. Даны матрицы A и B. Найти матрицу 
Вариант 1 Вариант 2

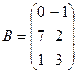


Вариант 3 Вариант 4




Вариант 5 Вариант 6

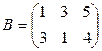


Вариант 7 Вариант 8

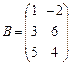


Вариант 9 Вариант 10



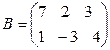
Задача 2. Найти матрицу, обратную матрице А

| 
|
| Вариант 1 | Вариант 2 |

| 
|
| Вариант 3 | Вариант 4 |

| 
|
| Вариант 5 | Вариант 6 |

| 
|
| Вариант 7 | Вариант 8 |
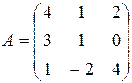
| 
|
| Вариант 9 | Вариант 10 |
Задача 3. Найти определитель произведения двух матриц 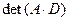 и
и  .
.
Вариант 1 

Вариант 2 

Вариант 3 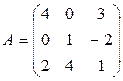

Вариант 4 

Вариант 5 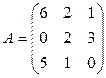

Вариант 6 

Вариант 7 
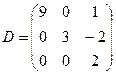
Вариант 8 

Вариант 9 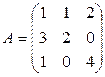

Вариант 10 

Задача 4. Найти ранг матрицы

| 
|
| Вариант 1 | Вариант 2 |

| 
|
| Вариант 3 | Вариант 4 |

| 
|
| Вариант 5 | Вариант 6 |

| 
|
| Вариант 7 | Вариант 8 |

| 
|
| Вариант 9 | Вариант 10 |
Задача 5. Записать систему уравнений в матричном виде и решить ее как матричное уравнение.
Вариант 1 Вариант 2 Вариант 3

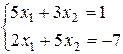

Вариант 4 Вариант 5 Вариант 6



Вариант 7 Вариант 8 Вариант 9



Вариант 10

Задача 6. Решить систему уравнений методом Гаусса
Вариант 1 Вариант 2 Вариант 3


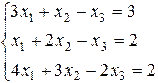
Вариант 4 Вариант 5 Вариант 6
|
|
|



Вариант 7 Вариант 8 Вариант 9
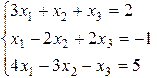


Вариант 10

Контрольное задание 2
Задача 1. Представить вектор x в виде линейной комбинации векторов a1, a2, a3, если система векторов a1, a2, a3 линейно независима. В случае линейной зависимости векторов a1, a2, a3 заменить один из них на вектор x так, чтобы полученная система стала линейно независимой.

Вариант 1 Вариант 2




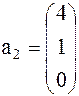

Вариант 3 Вариант 4






Вариант 5 Вариант 6

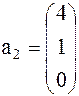




Вариант 7 Вариант 8

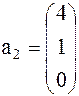


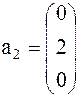
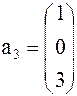
Вариант 9 Вариант 10

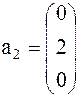




Задача 2. Найти матрицу линейного преобразования, переводящего каждый вектор x двухмерного линейного пространства в вектор y по следующему алгоритму:
| Вариант 1. | Симметричное отображение относительно прямой x1 = 0, а затем поворот на 90° по часовой стрелке. |
| Вариант 2. | Симметричное отображение относительно прямой x2 = 0, а затем поворот на 90° против часовой стрелки. |
| Вариант 3. | Симметричное отображение относительно прямой x1 = 0, а затем симметричное отображение относительно прямой x2 = 0. |
| Вариант 4. | Симметричное отображение относительно прямой x2 = 0, а затем симметричное отображение относительно прямой x1 = 0. |
| Вариант 5. | Симметричное отображение относительно начала координат, а затем поворот на 90° против часовой стрелки. |
| Вариант 6. | Симметричное отображение относительно прямой x2 = 0, а затем симметричное отображение относительно начала координат. |
| Вариант 7. | Симметричное отображение относительно начала координат, а затем симметричное отображение относительно прямой x1 = 0. |
| Вариант 8. | Симметричное отображение относительно начала координат, а затем симметричное отображение относительно прямой x2 = 0. |
| Вариант 9. | Поворот по часовой стрелке на 90°, а затем симметричное отображение относительно прямой x2 = 0. |
| Вариант 10. | Симметричное отображение относительно прямой x1 = 0, а затем поворот на 90° против часовой стрелки. |
Задача 3. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей
Вариант 1 Вариант 2 Вариант 3


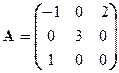
Вариант 4 Вариант 5 Вариант 6
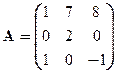


Вариант 7 Вариант 8 Вариант 9
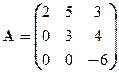

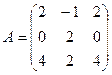
Вариант 10

Задача 4. Данную квадратичную форму записать в матричном виде, привести к каноническому виду и выписать матрицу соответствующего линейного преобразования.
|
|
|
Вариант 1.  .
.
Вариант 2.  .
.
Вариант 3.  .
.
Вариант 4.  .
.
Вариант 5.  .
.
Вариант 6.  .
.
Вариант 7.  .
.
Вариант 8.  .
.
Вариант 9.  .
.
Вариант 10.  .
.
Задача 5. Даны вершины треугольника  . Составить: а) уравнения медианы и высоты треугольника
. Составить: а) уравнения медианы и высоты треугольника  , проведенные из вершины
, проведенные из вершины  ; б) уравнение биссектрисы внутреннего угла
; б) уравнение биссектрисы внутреннего угла  .
.
| A | B | C | |
| Вариант 1 | (3,1) | (-13,-11) | (-6,-3) |
| Вариант 2 | (26,-5) | (2,2) | (-2,-1) |
| Вариант 3 | (-2,3) | (-18,-9) | (-11,15) |
| Вариант 4 | (6,8) | (-1,-2) | (1,-7) |
| Вариант 5 | (5,4) | (3,-9) | (-12,8) |
| Вариант 6 | (14,-2) | (11,8) | (15,-6) |
| Вариант 7 | (-21,4) | (4,10) | (-6,7) |
| Вариант 8 | (-3,-4) | (8,-7) | (16,12) |
| Вариант 9 | (22,8) | (4,14) | (-5,9) |
| Вариант 10 | (-8,-7) | (6,16) | (-4,-14) |
Задача 6. Найти уравнение нормали, проходящей через начало координат, к плоскости Ax+By+Cz+D=0. Найти координаты точки пересечения плоскости и нормали. Записать уравнение плоскости в виде уравнения плоскости, проходящей через эту точку.
| A | B | C | D | |
| Вариант 1 | -1 | |||
| Вариант 2 | -1 | |||
| Вариант 3 | -2 | -4 | ||
| Вариант 4 | -2 | -1 | -4 | |
| Вариант 5 | -2 | -1 | -2 | |
| Вариант 6 | -1 | |||
| Вариант 7 | -1 | -3 | ||
| Вариант 8 | -2 | |||
| Вариант 9 | -1 | |||
| Вариант 10 | -1 | -3 | -3 |
|
|
|


