4.6. Измерение угла обрушения. 4.7. Определение коэффициентов внутреннего и внешнего трения

4. 6. Измерение угла обрушения

Тонкие и сверхтонкие порошки (с размером частиц менее 10 мкм) способностью к течению в обычном понимании не обладают - через воронку даже достаточно большого диаметра они не вытекают, но через достаточно широкую щель в опорной площадке обрушиваются сразу всей   массой вниз.  Это      характерно даже для порошков сферической формы [23]. Такие порошки при свободной засыпке образуют ступенчатые или слоистые формы,   При  этом нижние _CJIOИ порошrа раскидываются и взрыхляются

массой верхних, когда последние падают на них. Замерить угол естественного откоса у таких порошков практически невозможно, поэтому их целесообразно характеризовать углом обрушения, как и все порошки с плохой текучестью.

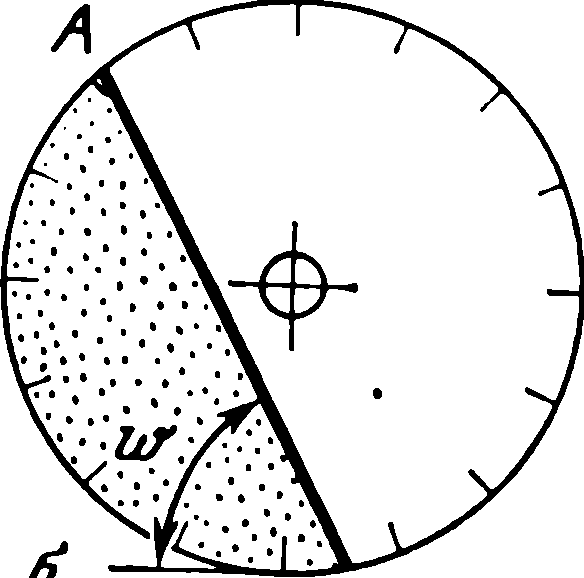
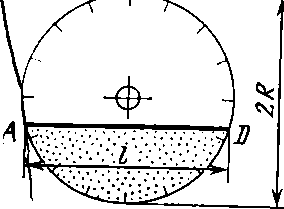
Для измерения  угла обрушения предлагается следующий способ [24]. Порошок засыпается в емкость прямоугольнфй формы из прозрачного материала (оргстекло и т. п. ), снизу снабженную пластинкой, перекрывающей выходную щель прибора. После открывания щели и прекращения высыпания части пробы вниз через прозрачную стенку рабочей емкости измеряется угол ψ _, который и является углом обрушения данного материала. Ценность этой несложной конструкции заключается в том, что она позволяет одновременно замерить и другие угловые характеристики - угол естественного откоса а и угол внутреннего трения ϕ

Другой интересный способ определения угJ1а обрушения [32]

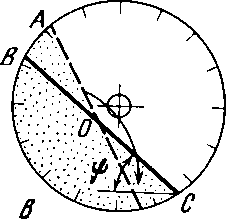
{рис. 4. 7) позволяет по сути дела измерять два предельных значения угла обрушения ω и ψ ). Способ заключается в следующем: порошок засыпается на одну треть емкости в цилиндрический барабан с прозрачной торцевой стенкой ишероховатой внутренней поверхностью; барабан очень медленно вращается, и прозрачный торец его наблюдается через оптическое устройство с измерительной угловой шкалой (точность замера углов ±30)

 При определенном угле поворота ω (начальное значение угла обрушения) происходит обрушение первоначального сегмента и возникновение нового с углом меньшей величины. После этого вращение барабана прекращается и замеряется значение угла ψ - конечная величина угла обрушения.

Обрушение порошкового сегмента в барабане происходит путем сползания верхней половины откоса в виде треугольной призмы ОВА и отложения сыпучей массы в нижней половине откоса в виде равновеликой треугольной призмы ОСД, как это показано на рис. 4. 7. Определение углов обрушения может быть использовано для вычисления угла внутреннего трения, о чем будет сказано в следующем разделе. Конструкция установки позволяет многократно повторять испытания на одной итойже порошковой пробе.

4. 7. Определение коэффициентов внутреннего и внешнего трения

Коэффициент внутреннего трения в механике сыпучих материалов для грунтов, горных пород, грузов [28, 29, 31] определяется по сопротивлению сыпучей среды деформации сдвига. При этом, как правило, не принимается во внимание сила сцепления между частицами, т. е. делается допущение, что сыпучая среда представляет собой среду идеальную, в которой  противодействие сдвигу определяется только преодолением нормального  усилия.

Кроме того, при статистическом обобщении сил трения отдельных частиц в материале, которые создают измеряемую  

а·

. о

\                                                   . D

Рис. 4. 7. Схема обрушения порошка n барабане

а - исходное состояние; б - состояние предельного равновесия; в - обрушение верхней половины откоса

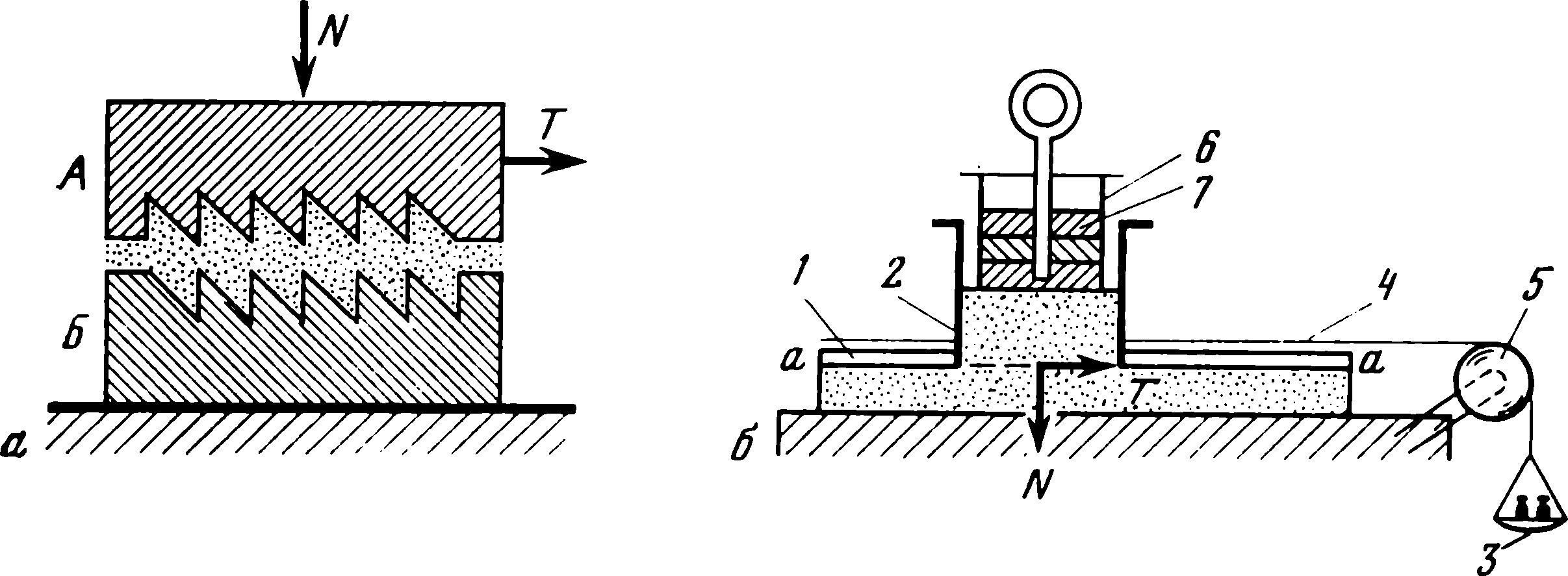
Рис. 4. 8. Схема (а) и прибор (б) для определения коэффициента внут­ реннего трения

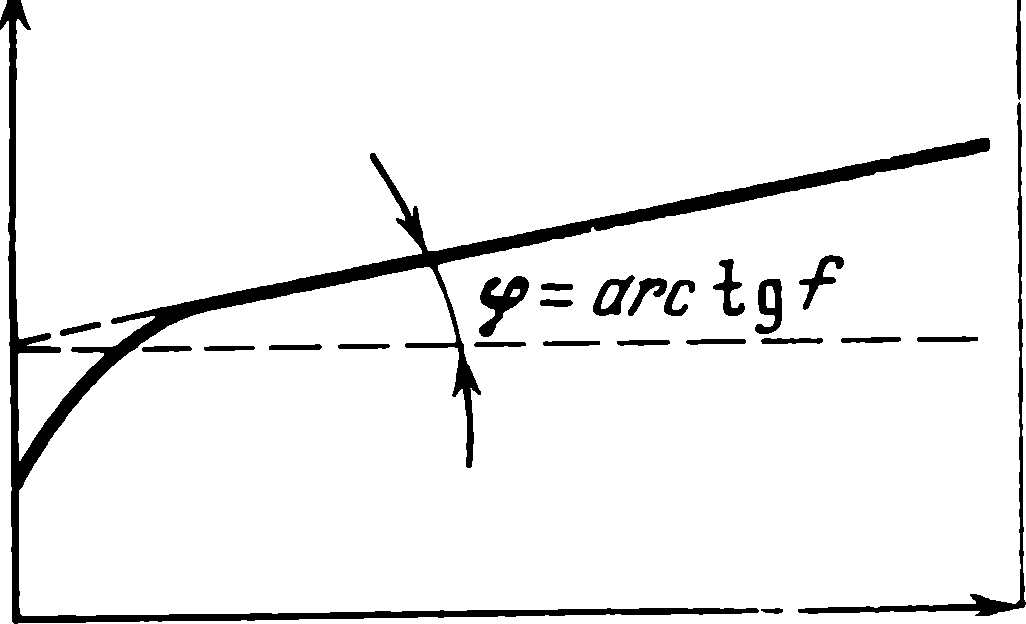а: А -  подвижная часть, Б -  нсподвиж-         Т--------------------------------------------------------,

ная основа; N - нормальная нагрузка [11), б: 1 - полный' закрепленный на столе желоб; 2-   коробна без днища; 3 - чашечка для грузов; 4 - шнур; 5 - блок 6 - рамка; 7 - прижимные пластины

Рис. 4. 9. Характер зависимости

сдвигающего усилия Тот нормальной нагрузки N

N

вокупную силу трения, предполагается условное существование реальной силы, непрерывно распределенной по поверхности всей совокупности частиц [29]. Это второе допущение связано уже с представлением дисперсного материала как сплошной среды.

Приняв эти ограничения, введем понятие коэффициента внутреннего трения. Если Т - сдвигающее усилие, N - нормальное (рис. 4. 8, а), которые приложены к системе в целом, то

Т = fN,                                                                                                            (4. 10)

где f - некоторый коэффициент пропорциональности, который и называется коэффициентом внутреннего трения.

На рис. 4. 9 [11] в прямоугольных координатах изображена типичная зависимость Т от N, откуда видно, что коэффициент

 

внутреннего трения f может быть определен в соответсвии с

(4. 10) как tgϕ где ϕ - угол внутреннего трения. В механике сыпучих сред он определяется как угол между предельными касательными и нормальными к сдвигающим усилиям напряжениями.

Определение угла внутреннего трения, таким образом, дает возможность вычислить как его тригонометрическую функцию значение коэффициента внутреннего трения порошка, который считается основным физико-механическим параметром любого сыпучего материала. Учитывая относительность определения этих величин, правильно было бы использовать их только для сравнительной оценки, не говоря уже о том, что сравнение числовых значений, определенных различными методами, не представляется возможным.

В предыдущем разделе говорилось о приспособлении несложной конструкции [24] для определения угла внутреннего трения по углу откоса ϕ порошка, оставшегося в емкости после высыпания некоторой его части.

В том же разделе описана конструкция  вращающегося бара­ бана для определения угла обрушения [32]. По определенным в соответствии с вышеописанным методом углам ω и ψ возможно вычислять угол внутреннего трения ϕ исилы сцепления между частицами С. Выведенные соотношения получены на основании приминения законовмеханики сплошных сред к результатом эксперемента:

 

 

 

ϕ = ψ – acrtgx                                                                                        (4. 12)

 

где R - радиус барабана; l - длина откоса; _Сн - насыпная плотность. Применение этой конструкции прибора для металлических порошков удобно еще и потому, что барабан может быть снабжен нагревателем в виде навитой спирали, позволяющим испытывать порошки при повышенных температурах до 600°С. Контроль температуры осуществляется с помощью термопары, погруженной прямо в порошок.

Для определения коэффициента внутреннего трения может быть применен прибор для испытания горных пород [29], кото­ рый пригоден для металлических порошков. Схема прибора дана на рис. 4. 8, б. Коробка без днища, движущаяся по полому неподвижному желобу с направляющими а-а, засыпается порошком так, чтобы он заполнил нижнюю часть ее объема. Полое пространство внутри желоба до самых направляющих

 

такжее засыпается порошком. На ровную поверхность порошка в коробке помещают рамку с прижимными пластинками, вес которых строго определен. Затем на весовую чашку, соединенную с коробкой шнуром, перекинутым через блок, постепенно

добавляют гири до тех пор, пока коробка не начнет двигаться вдоль желоба. Сопротивление движению пустой коробки, равно как и сопротивление вращению блока, через который перекинут шнур, компенсируется заранее подобранными добавочными разновесами при незаrруженном порошком приборе.

Для определения угла внутреннего трения сначала рассчитывают нормальные и касательные напряжения по плоскости сдвига. Первые вычисляются по формуле

t

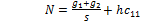                                                                                     (4. 13)

где g_{1 -} вес рамки; g₂ - вес прижимных пластин; S - площадь сечения коробки; h - высота сыпучего материала в коробке; с11  -    насыпная  плотность  его.  Касательные  напряжения  выражаются соотношением

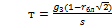                                                                   4. 14)                                 

где g₃ – вес гирек па чашке (за вычетом веса гирь, уравновешивающих собственное сопротивление движению блока и коробки); r_бл - коэффициент сопротивления вращению блока.

По вычисленным значениям строят график зависимости Т

от N, и по нему определяют тангенс угла наклона кривой к оси N, т. е. коэффициент внутреннего трения, и сам угол внутренне­ го трения по углу между кривой и осью N.

Поскольку величина коэффициента внутреннего трения является очень важной физико-механической характеристикой сыпучего материала [19, 20, 28], то предпринимаются попытки

 найти аналитическую форму его выражения через другие порошковые параметры. При этом второе ограничение, о котором говорилось в самом начале раздела, снимается, так как дисперсный материал рассматривается как таковой, а не как сплошная среда. В наиболее общем виде выражена зависимость коэффициента внутреннего трения идеально сыпучего материала через плот­ность укладки частиц порошка К [19]. Эта зависимость имеет пока характер первого приближения, но выражение коэффициента внутреннего трения через параметр К, зависящий от размеров частиц исостояния их поверхности, придает этому соотношению универсальный характер:

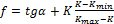                                                                  (4. 15)

где а - угол естественного откоса; А - постоянная; К - фактическая плотность укладки сыпучей среды; Kmin = сН/с_пик; Kmax = с_у/с_цик

Определяя экспериментально величину коэффициента внутреннего трения, существенно при этом оценивать ее взаимосвязь с другими параметрами порошка (хотя бы в границах эксперимента), причем в первую очередь с теми, которые определяют его сопротивление сдвиговой деформации [20]. Таковыми являются форма частиц (характеризуется коэффициентом формы ϗ ) и плотность укладки, поскольку именно они влияют сильнее всего на число контактов и суммарную площадь этих контактов в порошке. Установлена зависимость коэффициента внутреннего трения не только от указанных факторов, но также и от величины среднего диаметра частиц и коэффициента вариации:, который характеризует диапазон полидисперсности материала, т. е.

f = f (α, ϗ , к, η ).                                                                                           (4. 16)

Получение по результатам эксперимента даже частной формы подобной зависимости, справедливой для определенных диапа­ зонов указанных параметров, дает возможность некоторой объ­ ективной оценки физико-механических свойств порошков хотя бы в ограниченных пределах.

Известна зависимость между относительной плотностью ук­ ладки частиц θ (в % ) и коэффициентом внутреннего трения tgϕ , выраженная через коэффициент бокового давления компактного, но непрессованного материала [27]

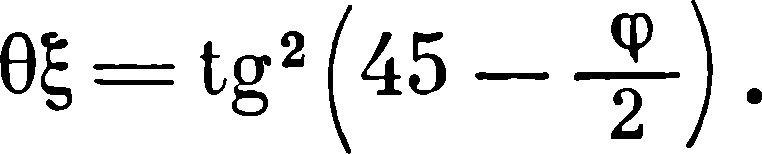                                                                                (4. 17)

Для медных порошков получено [11] хорошее совпадение результатов эксперимента с теоретическими: расчетами по формуле (4. 17).

Коэффициент внешнего трения характеризует взаимодействие порошка на границе порошок - стенка [19]. Явление это представляет собой весьма сложный и мало исследованный процесс, ни природа которого, ни закономерности до сих пор как следует не изучены. Количественная оценка этого коэффициента возможна на основе тех же методов, которые используются для сыпучих горных пород. В последних эта характеристика определяется при помощи приборов, называемых трибометрами, которые бывают с наклонной рабочей поверхностью (трибометры самотечного действия) и горизонтальной (трибометры с принудительным перемещением).

Трибометры первого типа представляют собой наклонную плиту, вмонтированную в плоскую коробку с вертикальными бортиками [29]. Угол наклона плиты может изменяться от 0 до 60°, что определяется по укрепленному на приборе  угломеру. Порошок засыпается на плиту тонким слоем, и  плита  поднимается. Угол, при котором начинается скольжение порошка, фиксируется специальной защелкой. Он и является углом внешнего трения, а тангенс его - коэффициентом внешнего трения порошка. Трибометр с горизонтальной рабочей поверхностью может

быть выполнен на основе уже описанной установки для определения коэффициента внутреннего трения (см. рис. 4. 8, б) с той лишь разницей, что на направляющие желоба, по которому движется емкость без дна с засыпанным порошком, укладывается полоса какого-либо материала (сталь, дерево), так что сдвиг

коробки теперь будет характеризовать силы трения скольжения между частицами порошка и материалом полосы, по которой движется заполненная порошком коробка. Вся методика выполнения эксперимента и расчета полученных данных сохраняется в том же виде, как было описано ранее.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: