 |
4.11. Испытания на спекаемость
|
|
|
|
4. 11. Испытания на спекаемость
Процесс спекания является весьма сложным, включающим в себя многообразные физические процессы [4, 12-18, 27], механизму
протекания которых посвящено большое число работ [18, 27, 58, 59]. Основным результатом процесса спекания являются сокращение поверхности (внутренней и внешней), снятие напрюнений в объеме образца, коагуляция пор, переход в более устойчивое термодинамическое состояние.
Для большинства металлов температура спекания лежит в пределах 60-75% от температуры плавления [27]. Поэтому для практической оценки спекаемости выбирают две-три температуры в этом диапазоне и, предварительно оценив геометрические размеры и плотность спрессованных образцов, спекают их нрп выбранных температурах. После спекания снова замеряют плотность и размеры образцов, по которым рассчитывают усадку их в результате спекания [4, 15].
Спеченные материалы часто исследуют металлографическими
И механическими методами - испытания на изгиб, растяжение (сжатие). Сопоставлением полученных данных с исходно заданными требованиями судят об удовлетворительном или неудовлетворительном эксплуатационном характере порошка.
Наглядной иллюстрацией исследования спекаемости являются кривые, приведенные на рис. 4. 16, которые выражают характер изменения объемной усадки и относительной плотности в зависимости от температуры и длительности спекания для образцов, спрессованных из порошков Мо различной дисперсностью [60]. Размер частиц порошков определяется средней величиной 10- 14 мкм и 1-2 мкм. Характер полученных зависимостей свидетельствует о повышенной интенсивности протекания процесса спекания в образцах из тонкодисперсного материала. После спекания
|
|
|
Рис. 4. 16. Диаграммы спекасмости
а - температурная зависимость объемной усадки (спекание 1 ч в водороде): 1 - порошок с частицами 1-2 мкм; 2- порошок с частицами 10-14 мкм; 6 - зависимость относительной плотности от температуры. спекания; в, г - кинетика изотермического спекания порошков с размером частиц 1-2 мкм (в) и с 10-14 мкм (г)
его в течение 1 ч при 1400°С достигается относительная плотность спеченных образцов порядка 94%.
Подобные зависи юсти дают возможность оценить все наиболее важные параметры спекания (температуру, выдержку, предполагаемую плотность и изменение размеров) исследуемого порошка. Подбор температуры спекания, скорости нагрева и атмосферы, как правипло, определяется конкретно в зависимости от грансостава, химической однородности, способа прессования, удельной нагрузки при прессовании и величины прессовок.
Спекаемость оценивается также и по механическим свойствам спеченных брикетов, и по изменению величины зерна в них в зависимости от режимов и условий процесса спекания [61].
Глава пятая
ФИЗИЧЕССИЕ ХАРАРТЕРИСТИКИ ПОРОШКОВ
Физические свойства порошков: электро- и теплопроводность, магнитные характеристики и другие - не являются физическими константами дисперсных материалов, ибо зависят от множества частных особенностей данного порошка - плотности, влажности, грансостава, окисленности, морфологических деталей и т. п., равно как и от условий проведения измерений. Ввиду этого физические характеристики порошков по большей части практически не поддаются стандартизации. Но их исследования служат важнейшей задаче изучения механизмов формирования твердых порошковых тел иоценке их технологической перспективности.
5. 1. Электрические характеристики
Важная роль порошковой металлургии в современной технологии вызвала к жизни наряду с классическими новые методы формообразования порошкового тела. И среди них - процесс электрического спекания пропусканием через образец электрического тока, генерирующего джоулево тепло, либо спекания с помощью индукционного нагрева.
|
|
|
В процессе электроспекания свойства образца и ресурсы источника тока должны быть соразмерны, для чего существенно важны величины электропроводности порошков [1, 2].
С другой стороны, при любых условиях формообразования центральными являются процессы возникновения и роста контактной поверхности между частицами порошка. Суммарная величина контактной поверхности, природа контактов даже в большей мере, нежели пористость тела, определяют все механические и физико-химические свойства готового изделия [3, 4], И одним из наиболее чувствительных индикаторов изменений межчастичных связей, числа и протяженности контактных площадок является электрическое сопротивление порошков. Иными словами, электросопротивление порошков может служить тонким инструментом исследования механизмов формирования твердого порошкового тела [4-16].
Отметим, что в свободном состоянии любой порошок, включая металлический, не пропускает электрический ток и понятие «электрическая проводимость» («электросопротивление») порошков приобретает смысл лишь в условиях, обеспечивающих межчастич ный контакт (сжатия или спекания).
С того момента как на рубеже двух столетий было обнаружено, что высокочастотный электрический импульс способен вызвать временное припекание двух твердых тел - фритт-эффект [1], предпринимались многократные попытки теоретического описания явления электрической проводимости пористых металлических тел.
Одно из направлений [12] в качестве исходной посылки рассматривает порошок в простейшем случае как двухфазную смесь металла с непроводящей (менее проводящей) фазой - пустотами между частицами.
Для статистических смесей изомерных и равноосных элементов фаз без ограничения их числа, концентрации, проводимости Оделевским выведено соотношение
(5. 1)
где λ см - проводимость смеси; λ i - проводимость i-фазы; θ - ее объемное содержание.
|
|
|
Для металлического порошка i = 1, 2, λ 2 = О, поэтому
λ см=λ 1(1-1. 5θ ). (5. 2)
Здесь λ 1 - электропроводность металла; θ - объемное содержание непроводящей фазы.
Экспериментальные измерения диэлектрической проницаемости пористых сегнетоэлектриков и теплопроводности алундовых материалов дали хорошее согласие с расчетами по уравнению (5. 1). Однако экспериментальная проверка формулы (5. 2) показала, что электропроводность порошков железа, меди, никеля, бронзы сильнее зависит от θ, нежели определяет уравнение (5. 2)
[12, 14]. Кроме того, оно ограничено областью 0< θ < 2/з.
В связи с этим были проведены более точные расчеты проводимости статистической смеси проводника с непроводником для произвольной концентрации фаз. Каждая фаза рассматривалась как смесь сферических, эллипсоидных и цилиндрических образований, а поле внутри частицы - фазы вычислялось как поле внутри сферы, поляризованной внешним полем.
В результате длинной цепи выкладок получены выражения
(5. 3)
(5. 4)
где gl1 и gl2 - доли объема соответственно проводящей и непроводящей фаз, приходящиеся на образование l сорта (упоминавшегося сферического, эллипсоидного и цилиндрического); kl1 и kl2 - коэффициенты соответственно для проводящей и непроводящей
фаз, зависящее от формы поляризуемых тел (образований). Уравнение (5. 3) используется при 0 < θ < 0, 5; (5. 4) –при 0, 5< θ < 1.
В результате расчетов была получена функция
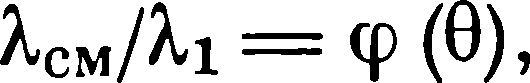(5. 5)
Экспериментальная проверка показала хорошее совпадение теории с практическими результатами, причем подобный расчет применим также к вычислению теплопроводности пористых металлических тел.
Функция (5. 5) является универсальной при отсутствии контактных и поверхностных явлений, но именно они часто сопровождают иопределяют электросопротивление порошкового тела. Для учета последнего соответствующее теоретическое направление рассматривает порошок как ансамбль проводящих частпц с располагающимися между нимипримесными переходными сопротивлениями, которые могут быть, например, представлены пленками окислов, покрывающих частицы [1-4, 6, 13-15, 17, 18]. Электрически они могут трактоваться как сеть статистически расположенных сопротивлений, распадающихся на 2 класса [1].
|
|
|
1. Сопротивление тела частиц, которое для металлов очень мало. От давления зависит незначительно, легко падает с его повышением. С ростом температуры, как и ддя массивных металлов, быстро возрастает. Не зависит от величины частиц, способа приготовления, силы и частоты тока при измерениях.
2. Сопротивление межчастичных контактов иповерхностных слоев. Ведет себя главным образом как полупроводник и может достигать значительных величин. Слабо зависит от давления ис повышением его резко падает, как и с ростом температуры. Увеличивается с уменьшением размера частиц. На него незначительное влияние при измерениях оказывает сила тока, с повышением которой переходное сопротивление снижается. Сильно зависит от способа препарирования образцов, изменяющего состояние, а с ним и сопротивление поверхностных слоев.
Расчеты проводимости смесей с несовершенными контактами между частицами [13, 14] базировались на выражении Хольма [19], описывающем сопротивление RKединичного контакта
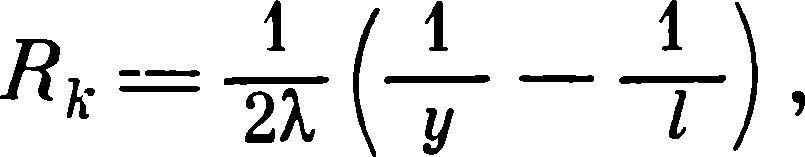(5. 6)
где λ - проводимость металлического вещества порошка; у- линейный размер контакта; l - линейный размер контактирующего тела. Если рассматривать l как линейный размер пленки,
окаймляющей частицу в зоне котакта толщиной δ и проводимостью λ *, то
имеем уравнения (5. 7), (5. 8), (5. 9).
Где χ =l/y, α - постоянный параметр. Проводимость смеси может быть нычис: rена из конечного выражения
где b - а - толщина пленки вокруг частицы с радиусом а.
Для практических расчетов λ см по формулам (5. 7) - (5. 10) необходимо знать линейный размер контакта у, вычисляемый из уравнения
(5. 11)
Где p – давление на контактную площадку между думя частицами:
| k k |
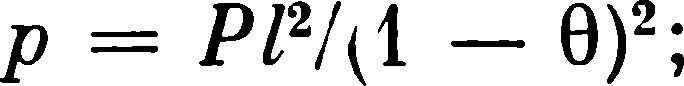(5. 12)
σ к- критическое напряжение на контакте; Р - среднее давление прессования в направлении нормали к площади образца.
В произвольном направлении
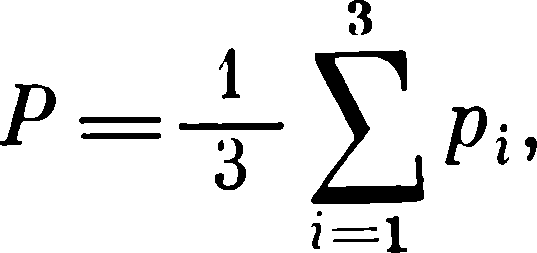
где Р1 внешнее давление; Р2 = Р3 =ξ P1; ξ - коэффициент бокового давления.
|
|
|
Из приведенных уравнений, зная размер контакта, можно вычислить электрическую проводимость (электросопротивление) порошка либо, наоборот, из данных измерения электросопротивления определить величину контактной площадки.
Сопоставление результатов расчетов с экспериментальными данными показало хорошее их согласие [13], например, для медных порошков.
В случае исследования процессов прессования и спекания
методом электросопротивления можно пользоваться также сравнительно простым показателем относительной величины возникающих межчастичных контактов [20-22]
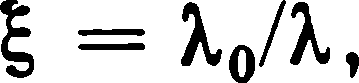(5. 14)
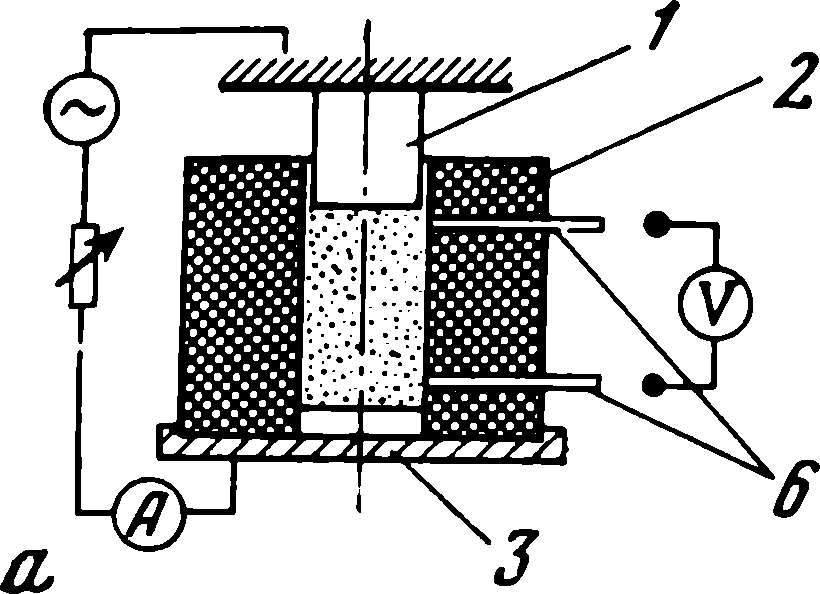
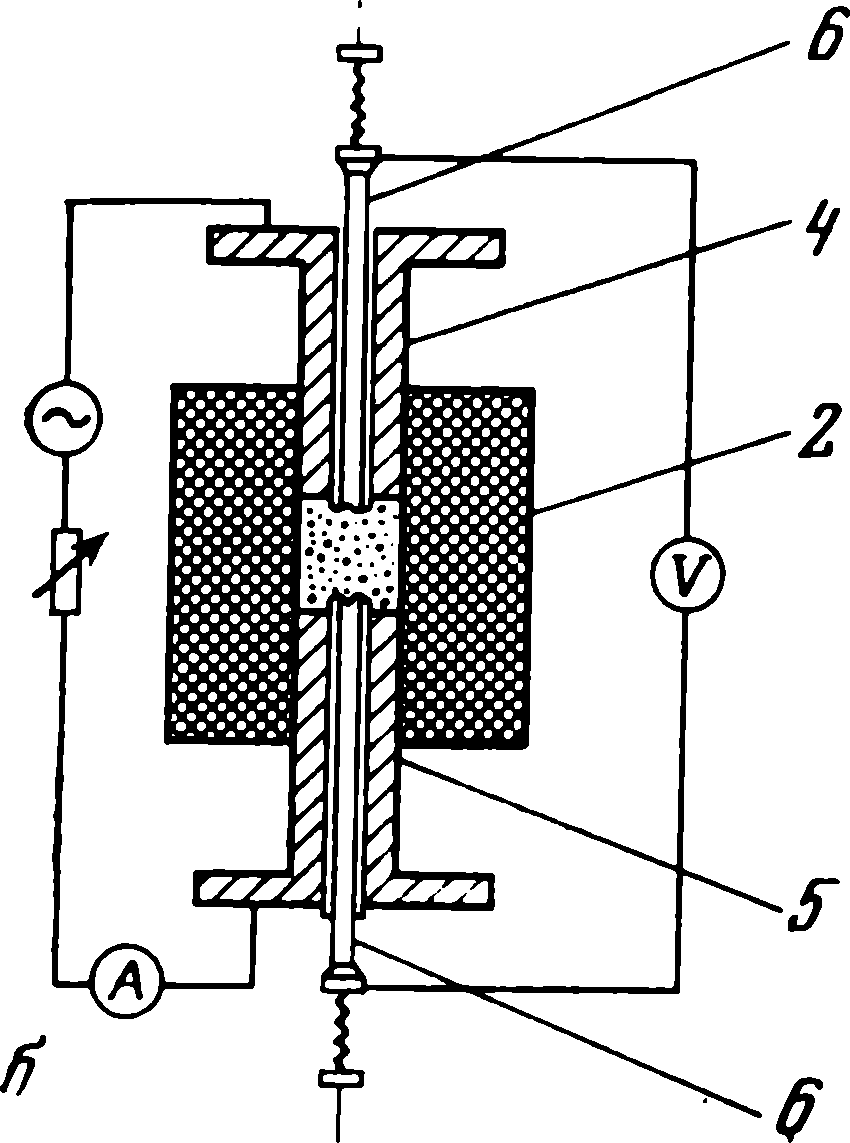
Рис. 5. 1. Схемы установок для измерения электросопротивления порошков
а- одностороннего прессования (применяется до давления 8 кбар при комнатной температуре); 6 - двустороннего сжатия (до давления 13 кбар) 1, 4, 5 - пуансоны
(4, 5 - верхний и нижний), 2 - матрица изолятор, з - дно, 6 - зонды; в - блок-схема: m - сжимаемый порошок, 1 - матрица, 2 - динамометр, з - вольтметр,
4 - индиrатор передвижения; 5 - зонды
где λ - удельная электропроводность металла порошка; λ 0-электропроводность образца, приведенная к нулевой пористости
λ 0 = λ обр/(1 - 1, 5θ ). (5. 15)
Для измерения величин электросопротивления порошков применяется несколько типов экспериментальных установок, имеющих в существе своем много общего [1. 4-6, 15-18, 23-25]. Порошок в них помещается в изолированную матрицу (рис. 5. 1) [1]. Ток подводится с торцов пуансонов - при двухстороннем прессовании (см. рис. 5. 1, 6) или еще и с днища матрицы (см. рис. 5. 1, а). Измерительная схема работает либо на компенсационном принципе с использованием одинарно-двойного моста постоянного тока, двойного моста Томпсона или Кельвина, либо с применением высокоомных вольтметров [25-31]. Падение напряжения ∆ U измеряется в процессе дискретно-непрерывного, ступенчатого прессования порошка. Величина его снимается с помощью горизонтальных (при одностороннем сжатии) либо вертикальных зондов (при двустороннем прессовании) (см. рис. 5. 1).
Одновременно с падением напряжения измеряются и сила прессования F, текущая высота слоя порошка h, сила подводимого
тока (см. рис. 5. 1, в) [1]. Из данных измерений рассчитываются:
Р = F/A, (5. 16)
Е = ∆ U/d, (5. 17)
ρ = m/Ah, (5. 18)
λ = I/АЕ, (5. 19)
где А - площадь сечения матрицы ипорошкового образца; d -
расстояние между зондами; т - масса порошка.
По результатам замеров электросопротивления R рассчитывается коэффициент электропроводности порошка:
(5. 20)
где d1 , d2 - диаметр цилиндров; h - высота слоя порошка.
Достоинством установки является возможность получения зависимости электропроводности не только от давления, но и от температуры в восстановительной, окислительной или нейтральной газовой среде.
Измерение электросопротивления может осуществляться не только описанным четырех- и двухзондовым методом, но и бесконтактным способом на кольцевых стандартных образцах [21, 27]. Как уще говорилось, электропроводность. находится в сложной зависимости от состояния, качества, природы собственно порошка, как и от условий эксперимента, и в первую голову от давления прессования [33] (рис. 5. 2, а) [1]. Это создает значительные трудности при сопоставлении результатов измерений, проведенных различными авторами. В каждом отдельном случае необходимо указывать, к какой деформационной области относятся полученные значения: к области А, где уплотнение по преимуществу происходит благодаря взаимному перемещению частиц (структурное уплотнение); к экспоненциальной области В, ДJIЯ которой характерны как упругая, так и пластическая деформации частиц; к области С закончившегося уплотнения, которая, собственно, уже не представляет порошок.
Другим вариантом сопоставительного анализа проводящих свойств металлических порошков мощет служить снятие данных измерения λ при θ = 0, 40 [25], когда силы межчастичного сцепления еще достаточно слабы, чтобы после снятия нагрузки образец вернулся в порошкообразное состояние.
Кроме того, необходимы возможно более подробная морфологическая характеристика порошка и данные по величине частиц и способу производства, которые оказывают самостоятельное влияние на величины электропроводности (см. рис. 5. 2) [34]. При этом известны случаи, когда морфологически идентичные порошки, обладающие одинаковым ситовым составом, обнаруживали совершенно различную проводимость ипричиной тому исключительно различие природы исвойств поверхностных (окисных) слоев.
В связи с последним электрическая проводимость может служить не только диагностическим признаком порошков, но и выполнять роль исследовательского зонда, позволяющего прощупывать тонкие детали механизма разрушения и восстановления окисных поверхностных пленок, обнажения металлических поверхностей и возникновения контактных мостиков металл-металл впроцессе сжатия порошка [4, 15, 35, 36].
Исследовательские возможности метода расширяются благодаря дифференциации вклада в электросопротивление поверхностных эффектов (разделение контактного ипленочного сопротивления Rа и сопротивления ядра частиц Ri) с помощью систематического изменения частоты тока [23]. А также благодаря измерениям температурного коэффициента электросопротивления [1, 5, 26]. Величины температурного коэффициента электросопротивления имеют и чисто практическое приложение к процессам спеrания и получения сверхпроводящих свойств (например, в ультрадисперсных средах), давая наряду со значениями электрической проводимости контрольный ряд цифр при изготовлении порошковых материалов специальногоназначения - для слаботочных или мощных контактов, сверхпроводников и термоэлектрических
материалов [37, 38].
|
|
|
