 |
ТЕМА № 1. ТОЧКА И ЕЕ ПРОЕКЦИИ
|
|
|
|
Рабочая тетрадь
По начертательной геометрии
Новочеркасск 2010
УДК 514 (07)
ББК 26.3
Рецензенты: док. техн. наук В.А. Евстратов
канд. техн. наук В.М. Фетисов
Составили: Чухно В.В.
Рабочая тетрадь по начертательной геометрии. Шахтинский институт (филиал) ЮРГТУ (НПИ) Новочеркасск: ЮРГТУ (НПИ), 2010, - 76 с.
Содержит основные тематические задачи начертательной геометрии и методику их решения.
© Шахтинский институт (филиал) ЮРГТУ (НПИ), 2010
© Чухно В.В. 2010
список Принятых обозначений
П1 – горизонтальная плоскость проекций
П2 – фронтальная плоскость проекций
П3 – профильная плоскость проекций
x, y,z – оси проекций
О – начало координат
 |
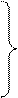А′, В′, С′,…
горизонтальные проекции точек
1′, 2′, 3,′…
 |
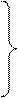А″, В″, С″,…
фронтальные проекции точек
1″, 2″, 3″,…
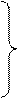А′″, В″′, С″′,…
профильные проекции точек
1′″, 2′″, 3′″,…
AB, CD, EF, l, t – обозначение прямых линий
α, β, γ, …, 
АВС – обозначение плоскости
f"оα, f"оβ, f"оγ, … – фронтальные следы плоскостей
h'оα, h'оβ, h'оγ, … – горизонтальные следы плоскостей
р"'оα, р"'оβ, р"'оγ, … – профильные следы плоскостей
h – горизонталь плоскости
f – фронталь плоскости
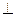– перпендикулярнось
∩– пересечение
– соединение
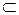– принадлежность
– совпадение
= – результат действия
. / – скрещиваемость
º/ – касание
Введение
Учебный процесс по дисциплине «Начертательная геометрия и инженерная графика» включает такие формы обучения, как лекции, практические занятия, самостоятельную работу студентов, программированный контроль знаний по темам курса, выполнение графических работ. На основании Государственного стандарта кафедра рекомендует практические занятия проводить на базе рабочей тетради. Дидактические материалы содержат задачи различной степени сложности. Задачи составлены на основе положений и выводов начертательной геометрии, являющейся теоретической базой курса.
|
|
|
Задачи имеют графическую основу для решения, следующую непосредственно за условием.
Все графические построения выполняются простым карандашом с применением простейших чертежных инструментов, а затем обводятся цветными карандашами или пастой (синий, зеленый цвет – вспомогательные построения, красный – конечный результат).
ТЕМА № 1. ТОЧКА И ЕЕ ПРОЕКЦИИ
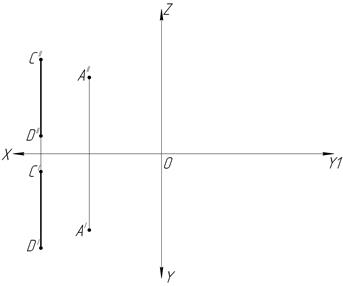
Две проекции точки (проекции на две взаимно-перпендикулярные плоскости) определяют положение точки в пространстве (рис.1).
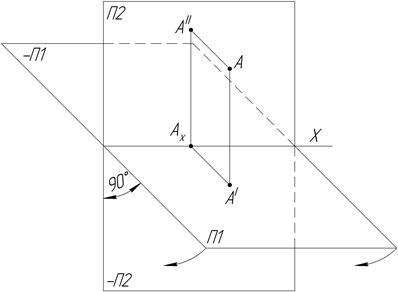
Рис.1
На практике часто для определения формы и размеров изображений на чертеже недостаточно двух проекций. В этом случае пользуются тремя взаимно перпендикулярными плоскостями (рис.2).
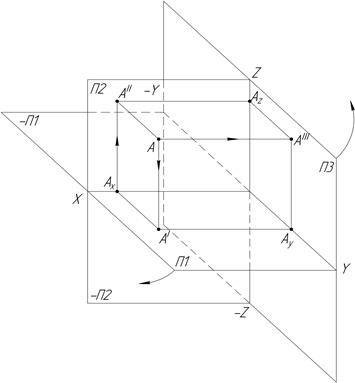
Рис.2
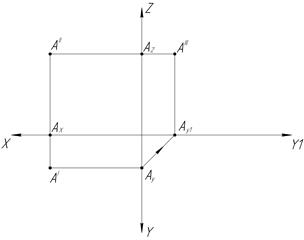
Рис.2 Продолжение
Для комплексного чертежа (эпюра) имеем следующие положения:
- фронтальная и горизонтальная проекции точки всегда находятся на одной вертикальной линии связи;
- фронтальная и профильная проекции точки всегда находятся на одной горизонтальной линии связи;
- расстояние от фронтальной проекции точки до оси ОХ измеряет высоту самой точки над горизонтальной плоскостью проекций П1, численное значение которой определяется координатой Z. Расстояние от горизонтальной проекции точки до оси ОХ измеряет расстояние самой точки до фронтальной плоскости проекций П2 и определяется координатой Y. Аналогично расстояние фронтальной проекции точки до оси OZ измеряет расстояние от точки до профильной плоскости проекций П3 и определяется координатой Х;
|
|
|
- по горизонтальной и фронтальной проекциям точки всегда можно построить ее профильную проекцию. Существует три способа построения: координатный (рис.3,а); проекционный (рис.3,б); с помощью постоянной прямой (рис.3,в).
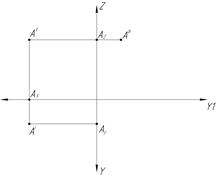
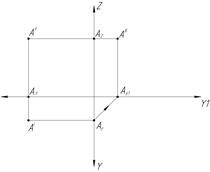
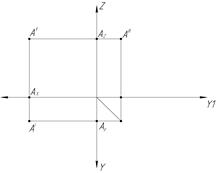
а) б) в)
Рис.3
З а д а ч и П О Т Е М Е 1
1. Постройте проекции точек A,B,C,D,E,F,K, если даны их наглядные изображения. Определите, в каких четвертях находятся точки.
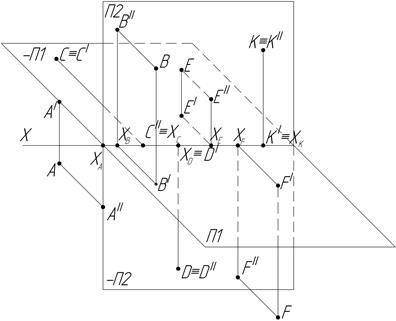
Заполните таблицу:
2. Постройте проекции точек А, В, С при условии: точка А находится на плоскости проекций П1; точка В удалена от плоскости П1 на 20мм, а от плоскости П2 на 25мм; точка С находится на плоскости П2 и удалена от плоскости П1 на 30мм.
3. Постройте: а) точку N, расположенную над точкой А на расстоянии 20мм; б) точку М, расположенную под точкой В на расстоянии 10мм.
4. В какой четверти будет находиться точка В, симметричная точке А, относительно плоскости П2? Постройте точку В.
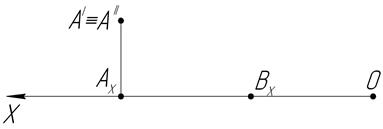
5. Постройте точку А, расположенную в I четверти пространства. Постройте эпюр точки В симметрично точке А относительно плоскости проекций П1. (Величины координат точки А возьмите произвольно.)
6. Представьте точку D, равноудаленную от плоскостей П1 и П2. Постройте эпюр точки Е симметрично точке D относительно оси ОХ. (Величины координат точки D возьмите произвольно.)
7. Достройте профильные проекции точек А, В, С, D на наглядном изображении этих точек и определите, в каких октантах они находятся.
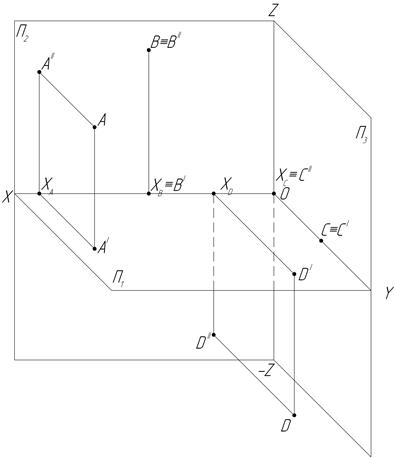
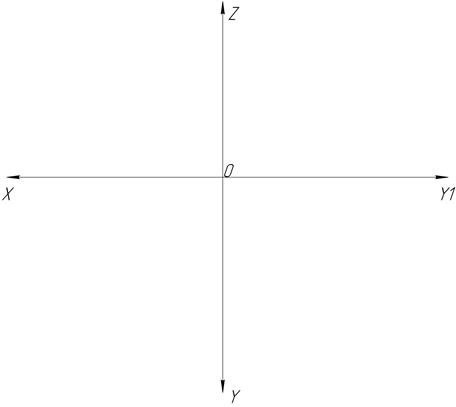
8. Достройте профильные проекции точек А,В,С. Определите, на каком расстоянии (в мм) находятся заданные точки от плоскостей проекций П1, П2, П3.
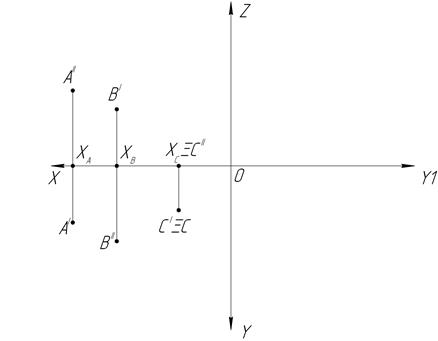
Заполните таблицу:
9. На каком расстоянии (в мм) находится точка А от осей проекций ОХ,OY,OZ?
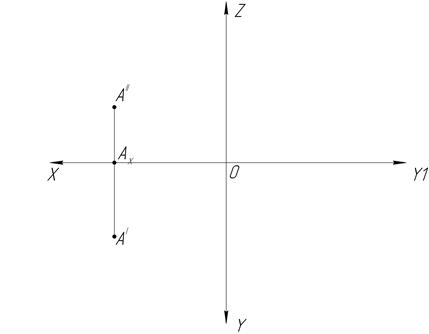
Заполните таблицу:
10. Постройте три проекции точек А, В, С и D:
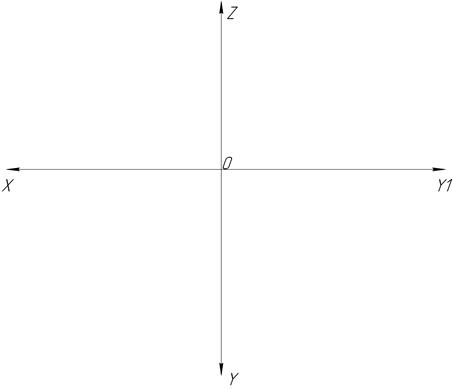А (15; 25; 30);
В (30; 10; 20);
С (40; 10; -15);
D (20; -30; -20).
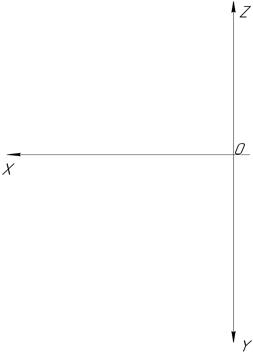11. Постройте две проекции треугольника, если даны координаты его вершин:
А (20; 40; 30);
В (60; 10; 50);
С (40; 60; 0).
ТЕМА № 2. ПРЯМАЯ ЛИНИЯ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ
ПРЯМОЙ. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ,
ПРЯМОЙ И ТОЧКИ
Отрезок прямой АВ определяет прямую, произвольно расположенную относительно плоскостей проекций П1, П2 и П3. Это означает, что углы наклона такой прямой к плоскостям проекций отличны от 0о и 90о и прямая называется прямой общего положения (рис.4).
|
|
|
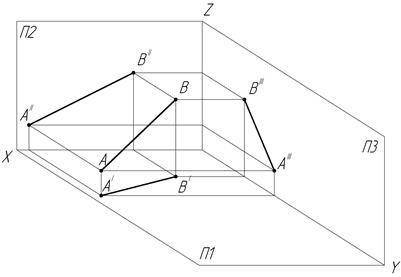
Рис.4
Отрезки прямой, расположенные параллельно одной из плоскостей проекций, называются прямыми частного положения – прямыми уровня (горизонтальная прямая параллельна плоскости П1; фронтальная прямая параллельна плоскости П2; профильная прямая параллельна плоскости П3).
Отрезки прямой, расположенные перпендикулярно одной плоскости проекций и параллельно двум другим, называются прямыми частного положения – прямыми проецирующими (горизонтально-проеци-рующая перпендикулярная плоскости П1 и параллельна П2 и П3); (фронтально-проецирующая перпендикулярная плоскости П2 и параллельна П1 и П3); (профильно-проецирующая перпендикулярная плоскости П3 и параллельна П1 и П2).
Прямая линия может пересекаться с плоскостями проекций, точки их пересечения называются следами (рис.5).
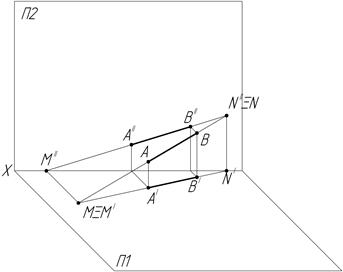
Рис.5
Натуральная величина отрезка прямой общего положения определяется величиной гипотенузы прямоугольного треугольника, построенного на одной из проекций, как на катите. Второй катет треугольника равен разности расстояний концов отрезка до разделяющей эти проекции оси (рис.6).
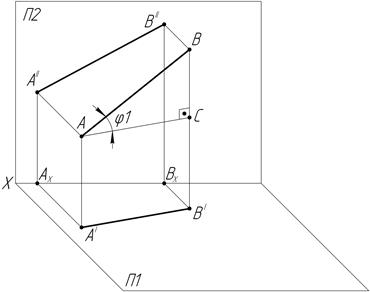
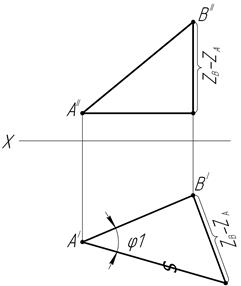
Рис.6
Две прямые линии в пространстве могут:
а) пересекаться (пересекающиеся прямые) (рис.7,а);
б) быть параллельными (параллельные прямые) (рис.7,б);
в) скрещиваться (скрещивающиеся прямые) (рис.7,в).
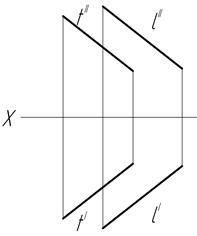
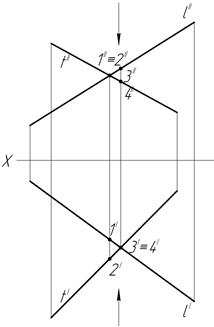
а) б) в)
Рис.7
Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол проецируется без искажения при условии, что вторая его сторона не перпендикулярна этой плоскости: ВС || П1, АВ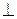 
П1, АВС=А'В'С'=90° (рис.8).
Рис.8
З а д а ч и П о Т Е М Е 2
12. Определите, как называются отрезки прямых АВ, СD, EF, MN, KL и PR? Определите натуральную величину этих отрезков и величины углов наклона φ1, φ2, φ3.
Заполните таблицу:
| Отрезки прямых | АВ | CD | EF | MN | KL | PR |
| Наименование | ||||||
| Величина в мм | ||||||
| Угол φ1 (град) | ||||||
| Угол φ2 (град) | ||||||
| Угол φ3 (град) |
|
|
|
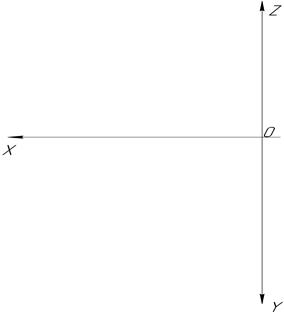
13. Постройте комплексный чертеж (эпюр) прямой АВ, проходящей через точку А (60;20;15) и В (20;10;10).
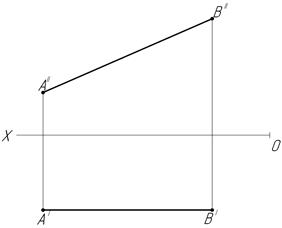
14. Постройте фронтальную прямую в I четверти пространства при условии, что она наклонена к плоскости проекций П1 (φ1) под углом, равным 45о.
15. Постройте профильно-проецирующую прямую при условии, что она равноудалена от плоскостей проекций П1, П2.
16. Постройте горизонтальную прямую при условии, что она расположена в IV четверти и имеет угол φ2=30о.
17. Постройте прямую, если известно, что она проходит через точку А(35;25;30) и перпендикулярна фронтальной плоскости проекций.
18. Постройте следы прямой линии АВ и определите:
- углы наклона к плоскостям проекций;
- через какие четверти пространства она проходит.
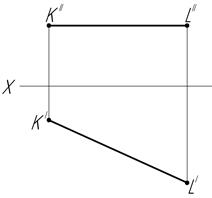
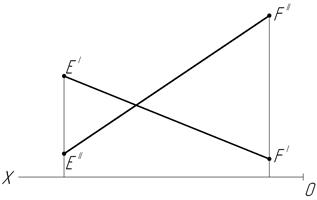
19. постройте следы М и N заданной прямой EF. Определите, через какие четверти пространства проходит прямая.
20. Постройте проекции прямой, если даны следы этой прямой. Определите, через какие четверти пространства проходит прямая.
21. Представьте прямую общего положения в IV четверти. Постройте проекции этой прямой, а затем следы M и N.
22. Постройте следы прямой АВ, определите:
- натуральную величину отрезка;
- углы наклона прямой к плоскостям проекций П1 и П2;
- укажите, через какие четверти пространства проходит прямая.
23. Определите натуральную величину отрезка АВ общего положения (в мм) и найдите величину угла φ1 (в град). Запишите ответы:
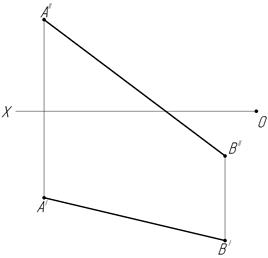
|AB|= 
φ1=
24. Определите натуральную величину отрезка CD общего положения (в мм) и найдите величину угла φ3 (в град). Запишите ответы:
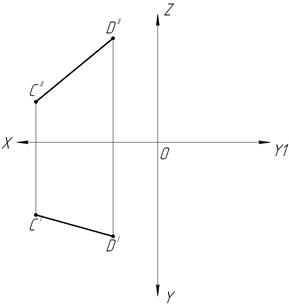
|CD|= φ3=
25. 
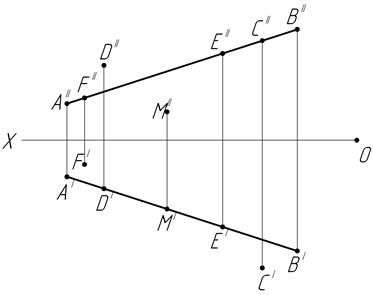Определите, как расположены точки D, E, C, F, M по отношению к отрезку прямой АВ.
Возможные ответы:
- выше АВ;
- ниже АВ;
- перед прямой;
- за прямой;
- 
АВ.
Заполните таблицу:
| Точки | D | E | C | F | M |
| Ответы |
26. Определите взаимное положение отрезков прямых AB и CD между собой.
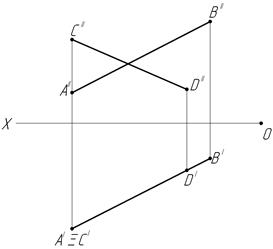
Ответ: АВ CD Ответ: АВ CD
Ответ: АВ CD
27. Через точку А проведите прямую параллельно прямой CD.
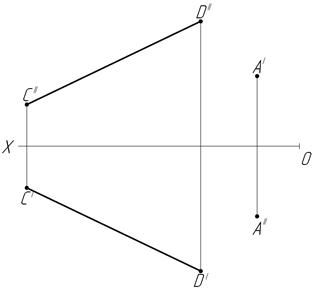
28. Через точку А проведите прямую, пересекающую прямые CD и FN.
29. Постройте прямую АВ общего положения в I четверти пространства, затем – точку Е во II четверти. Проведите через точку Е прямую до пересечения с АВ.
30. Определите натуральную величину расстояния от точки А до прямой CD (в мм).
|
|
|
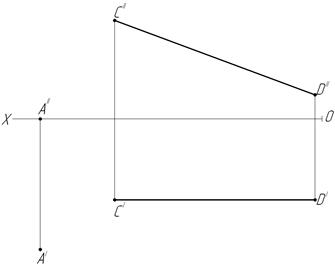
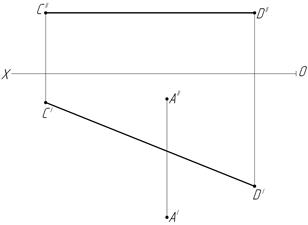
|AК|= |AК|=
|AК|=
31. Постройте горизонтальную прямую CD в III четверти. Определите натуральную величину расстояния от точки А, расположенной в I четверти, до прямой CD.
ТЕМА № 3. ПЛОСКОСТЬ. ПЛОСКОСТИ ОБЩЕГО И
ЧАСТНОГО ПОЛОЖЕНИЯ. ИХ СВОЙСТВА
Плоскость в пространстве может определяться:
§ тремя точками, не лежащими на одной прямой;
§ прямой и точкой, не лежащей на этой прямой;
§ двумя пересекающимися прямыми;
§ двумя параллельными прямыми;
§ плоской фигурой;
§ следами.
По отношению к плоскостям проекций плоскости называются общего положения и частного положения. Последние могут быть перпендикулярными к одной из плоскостей проекций (проецирующие) или к двум плоскостям проекций одновременно (уровня) (рис.9).
Плоскость общего Плоскость проеци- Плоскость уровня
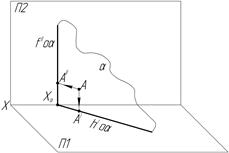
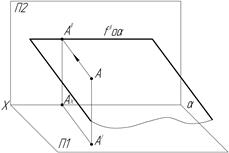
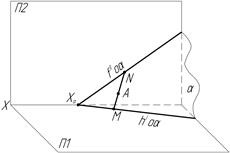положения рующая α 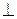П1 α || П1
Рис.9
Принадлежность прямой плоскости определяется принадлежностью двух ее точек данной плоскости, или принадлежностью одной точки и параллельностью прямой какой-либо прямой лежащей в плоскости.
Признаком принадлежности точки и прямой к плоскости частного положения является совмещение на экране их проекций со следами плоскости, обладающими собирательными свойствами.
К линиям особого положения (главным линиям плоскости) относятся горизонталь, фронталь, профильная прямая и линия наибольшего наклона плоскости: h 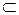α, h || П1, f 
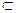α, f || П2, линия наибольшего наклона 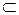MN α, MN 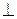h (рис10).
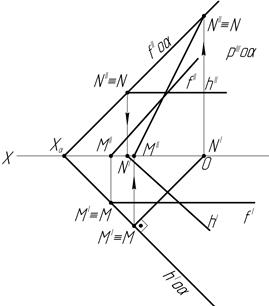
Рис.10
З а д а ч и П О т е м е 3
32. Определите, как расположены заданные плоскости по отношению к плоскостям проекций. Постройте точки, лежащие в этих плоскостях. Чему равны (в градусах) величины углов наклона φ1, φ2 и φ3.
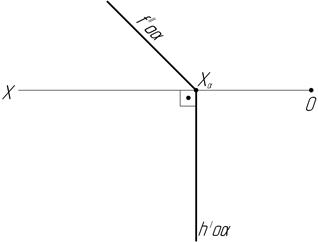
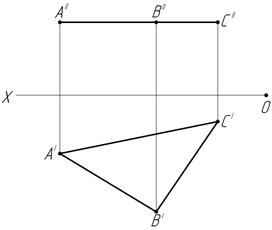
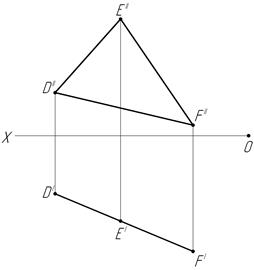
Заполните таблицу:
| Плоскости | ABC | DEF | α |
| Расположение | |||
| Угол φ1 (град) | |||
| Угол φ2 (град) | |||
| Угол φ3 (град) |
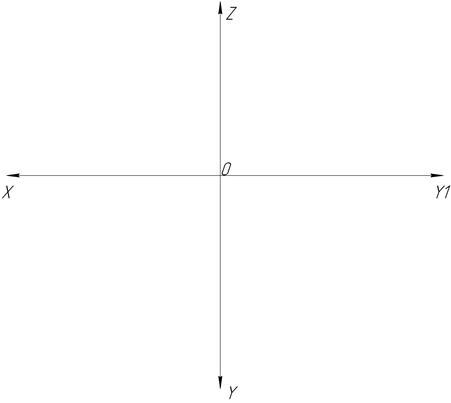
33. Как называется плоскость, углы наклона которой: φ1=90˚; φ2=90˚; φ3=0˚? Построить эпюр этой плоскости. Способ задания плоскости выбрать самостоятельно.
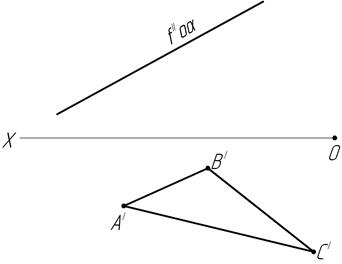
34. Постройте фронтальную плоскость, заданную ΔАВС, расположенную в IV четверти на расстоянии 20 мм от плоскости П2.
35. Постройте горизонтально-проецирующую плоскость, заданную параллельными прямыми, расположенную под углом φ2=45˚ в III четверти.
36. Постройте фронтальную проекцию ΔАВС, принадлежащую плоскости β, перпендикулярной фронтальной плоскости проекции.
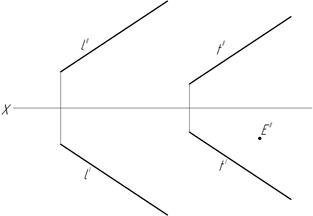
37. Определите принадлежность точек A, B, C, D, E заданной плоскости α.
Заполните таблицу:
| Точки | A | B | C | D | E |
| Принадлежность |
38. Точка Е принадлежит плоскости, постройте горизонтальную проекцию точки Е.
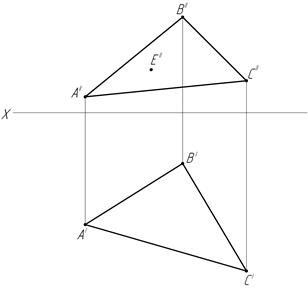
39. 
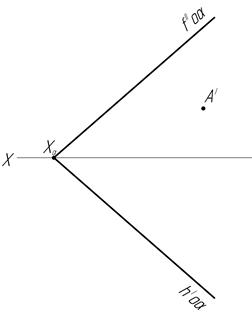
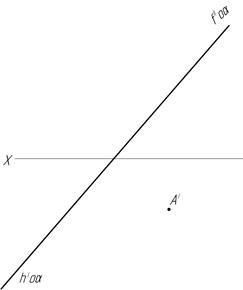Выполните необходимые построения и определите, в какой четверти находится точка А, если она принадлежит плоскости α.
а) б)
в)
40. Постройте следы плоскости, заданной:
а) пересекающимися прямыми;
б) параллельными прямыми;
в) плоской фигурой (ΔАВС).
41. В плоскости общего положения, заданной двумя пересекающимися прямыми, постройте: горизонталь, фронталь, линию наибольшего наклона.
42. В плоскости общего положения постройте горизонталь на расстоянии 20 мм от плоскости П1, фронталь на расстоянии 30 мм от плоскости П2 и линию наибольшего наклона плоскости.
43. 
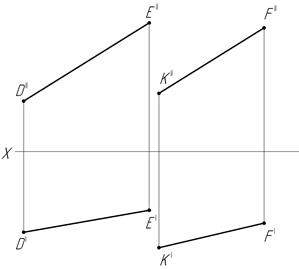Определите в градусах угол наклона заданной плоскости к плоскости проекций П1.
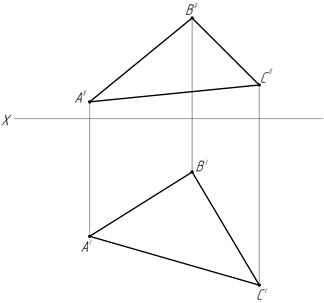
а) б)
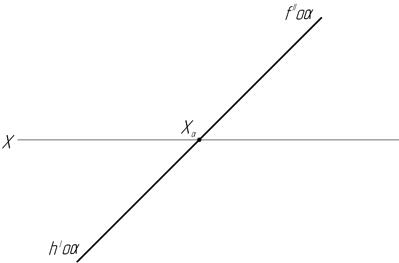
в)
ТЕМА № 4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Плоскости могут пересекаться (рис.11,а,б) или быть параллельными (рис.11,в).
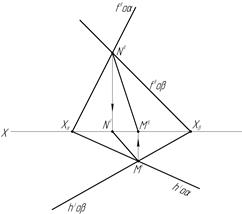
а)
б)
Рис.11
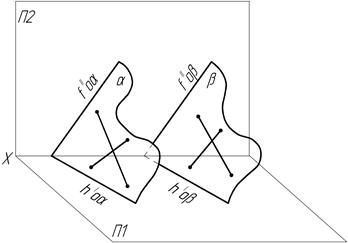
в)
Рис.11 Продолжение
Плоскости пересекаются по прямой линии, которая определяется по двум точкам, принадлежащим одновременно обеим плоскостям, либо по одной точке и направлению.
Если одна плоскость будет горизонтальной или фронтальной, то линией пересечения будет горизонталь или фронталь.
В общем случае линия пересечения двух плоскостей определяется методом вспомогательных плоскостей (чаще всего проецирующие, уровня). Определяется общая точка для всех трех плоскостей, она и принадлежит искомой линии пересечения двух плоскостей.
Признаком параллельности двух плоскостей является параллельность двух пересекающихся прямых одной плоскости двум пересекающимся прямым другой плоскости. Признаком параллельности плоскостей, заданных следами, является параллельность одноименных следов.
У параллельных плоскостей линии уровня взаимнопараллельны.
З а д а ч и П О т е м е 4
44. Найдите линию пересечения двух плоскостей.
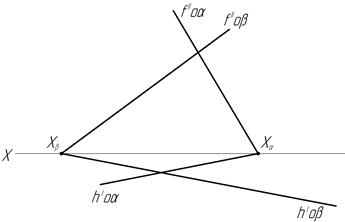
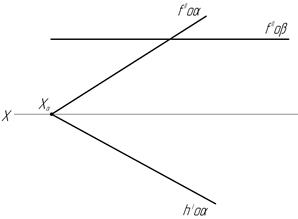
а) б)
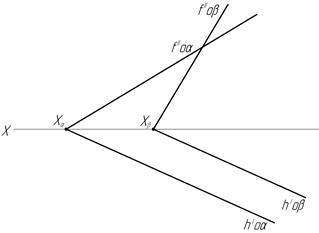
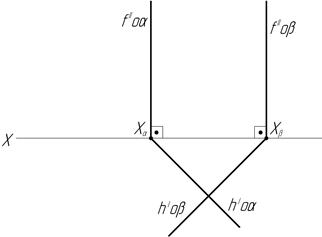
в) г)
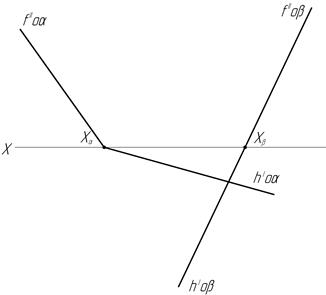
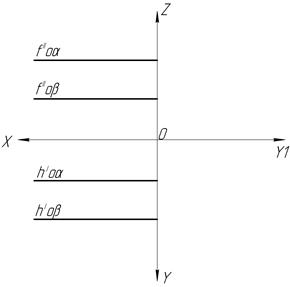
д) е)
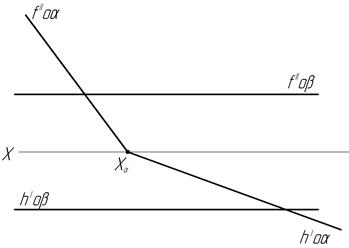
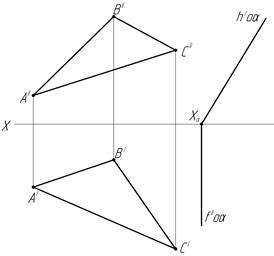
ж) з)
 |
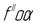
и) к)
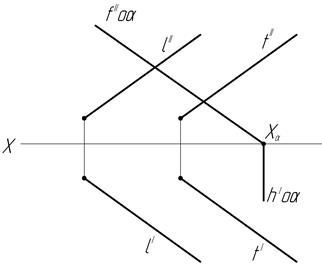
45. Через точку А проведите плоскость, параллельную заданной плоскости.
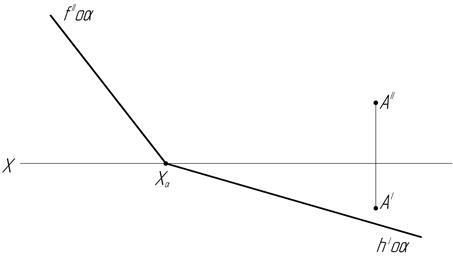
а)
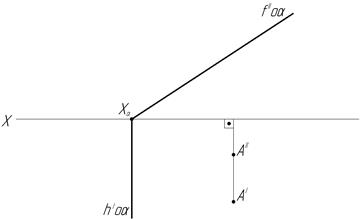
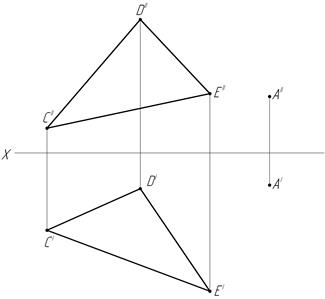
б) в)
ТЕМА № 5. ВЗАИМНОЕ ПОЛОЖЕНИЕ
ПРЯМОЙ И ПЛОСКОСТИ
Точка пересечения прямой с плоскостью (точка встречи) определяется как точка, принадлежащая одновременно прямой и плоскости (рис.12).
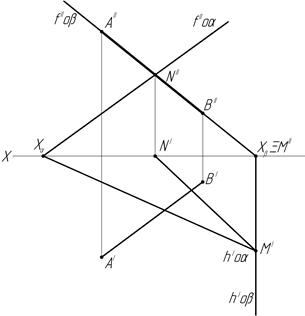
Рис.12
Для построения точки пересечения прямой линии с плоскостью общего положения необходимо выполнить три этапа построения:
1) через заданную прямую провести вспомогательную плоскость (проецирующую или уровня);
2) построить линию пересечения заданной плоскости с вспомогательной;
3) определить положение точки пересечения заданной прямой с заданной плоскостью, как точку пересечения найденной линии пересечения плоскости с заданной прямой.
Если плоскость частного положения, то проекции точки пересечения с прямой определяются в один этап, одна проекция ее будет находиться на пересечении следа, обладающего собирательными свойствами, а другая – на прямой, исходя из условия принадлежности точки прямой.
Признаком параллельности прямой и плоскости является параллельность заданной прямой какой-либо прямой, лежащей в плоскости (рис.13).
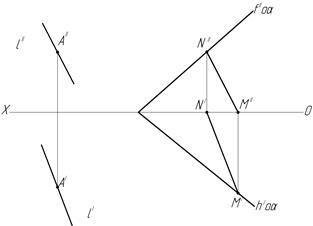
Рис.13
З а д а ч и П О Т Е М Е 5
46. Постройте точку пересечения прямой АВ с заданной плоскостью α:
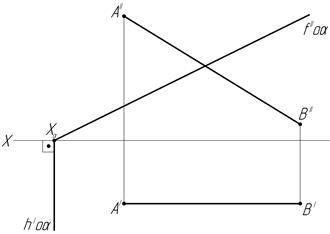
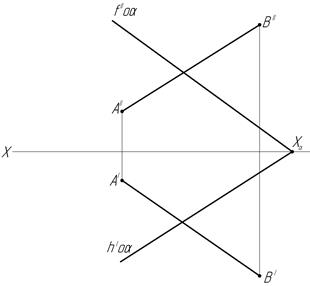
а) б)
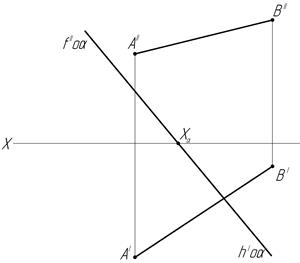
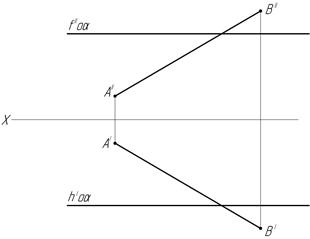
в) г)
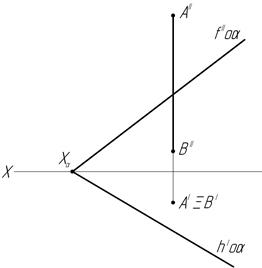
д) е)
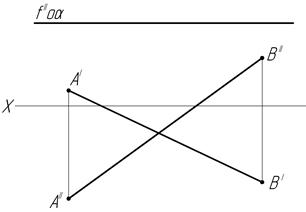
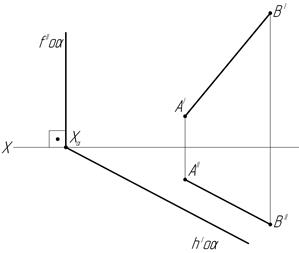
ж) з)
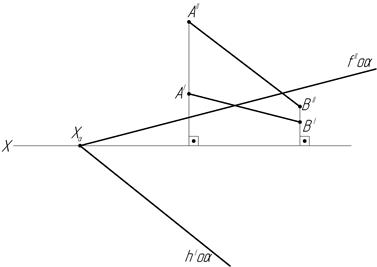
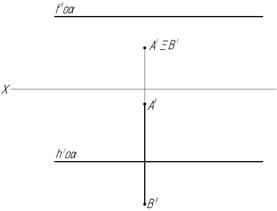
и) к)
47. Определите (в мм) координаты точки К – пересечения отрезка прямой АВ с заданной плоскостью:
|
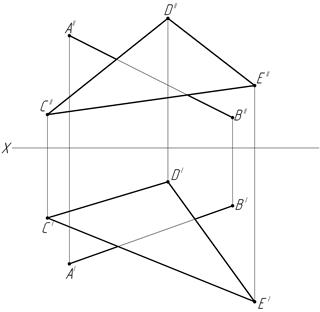Ответ: (·) К1 ()
|
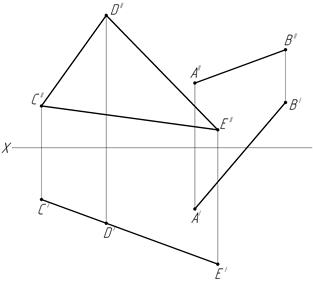Ответ: (·) К2 ()
|
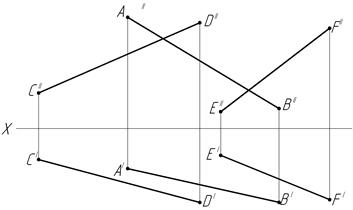Ответ: (·) К3 ()
48. Представьте фронтально-проецирующую плоскость, заданную двумя пересекающимися прямыми (CD 
EF) и расположенную в I четверти пространства. Отрезок прямой АВ общего положения расположен в IV четверти. Постройте точку пересечения прямой АВ с плоскостью (CD 
EF).
49. Через точку А проведите прямую общего положения, параллельную заданной плоскости.
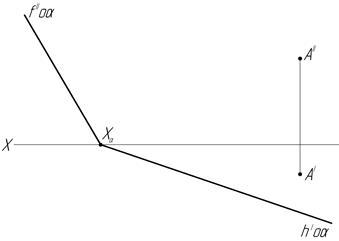
а) б)
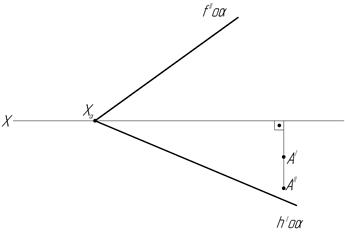
в)
50. Через точку А проведите плоскость общего положения, параллельную CD.
51. Через точку А, заданную в III четверти, проведите прямую, параллельную горизонтально-проецирующей плоскости α (ƒ″оα, h′оα).
|
|
|
